Multiplicity-Free Permutation Characters in GAP, part 2
THOMAS BREUER
Lehrstuhl D für Mathematik
RWTH, 52056 Aachen, Germany
May 30th, 2006
We complete the classification of the multiplicity-free permutation
actions of nearly simple groups that involve a sporadic simple group,
which had been started in [BL96] and [LM].
Contents
1 Introduction
2 The Approach
2.1 Computing Possible Permutation Characters
2.2 Verifying the Candidates
2.3 Isoclinic Groups
2.4 Tests for GAP
3 The Groups
3.1 G = 2.M12
3.2 G = 2.M12.2
3.3 G = 2.M22
3.4 G = 2.M22.2
3.5 G = 3.M22
3.6 G = 3.M22.2
3.7 G = 4.M22 and G = 12.M22
3.8 G = 4.M22.2 and G = 12.M22.2
3.9 G = 6.M22
3.10 G = 6.M22.2
3.11 G = 2.J2
3.12 G = 2.J2.2
3.13 G = 2.HS
3.14 G = 2.HS.2
3.15 G = 3.J3
3.16 G = 3.J3.2
3.17 G = 3.McL
3.18 G = 3.McL.2
3.19 G = 2.Ru
3.20 G = 2.Suz
3.21 G = 2.Suz.2
3.22 G = 3.Suz
3.23 G = 3.Suz.2
3.24 G = 6.Suz
3.25 G = 6.Suz.2
3.26 G = 3.ON
3.27 G = 3.ON.2
3.28 G = 2.Fi22
3.29 G = 2.Fi22.2
3.30 G = 3.Fi22
3.31 G = 3.Fi22.2
3.32 G = 6.Fi22
3.33 G = 6.Fi22.2
3.34 G = 2.Co1
3.35 G = 3.F3+
3.36 G = 3.F3+.2
3.37 G = 2.B
4 Appendix: Explicit Computations with Groups
4.1 24:A6 type subgroups in 2.M22
4.2 24:S5 type subgroups in M22.2
4.3 Multiplicities of Multiplicity-Free Actions of 6.Fi22.2
1 Introduction
In [BL96], the multiplicity-free permutation characters of the sporadic
simple groups and their automorphism groups were classified.
Based on this list,
the multiplicity-free permutation characters of the central extensions of the
sporadic simple groups were classified in [LM].
The purpose of this writeup is to show how the multiplicity-free
permutation characters of the automorphic extensions of the central
extensions of the sporadic simple groups can be computed,
to verify the calculations in [LM] (and to correct an error,
see Section 3.32),
and to provide a test file for the GAP functions and the database.
The database has been extended in the sense that also most of the character
tables of the multiplicity-free permutation modules of the sporadic simple
groups and their automorphic and central extensions have been computed,
see [Höh01,Mül03,BM05,Mül08] for details.
Five errors in an earlier version (from July 2003) have been pointed out by
Jürgen Müller.
These errors concern the numbers of conjugacy classes of certain
point stabilizers in 2.J2.2, 2.HS.2, and 6.Fi22.2
(see Sections 3.12, 3.14, and 3.33).
The only differences between the current version and the version that was
available since 2005 are additions of references,
adjustments of group names in the data file,
and adjustments of the GAP output format to version 4.5,
see [GAP24].
Note that the version from 2003 was based on a data file that contained only
the permutation character information, whereas the current version uses
the database file of [BM05],
which includes also the known character tables of endomorphism rings.
2 The Approach
Suppose that a group G contains a normal subgroup N.
If π is a faithful multiplicity-free permutation character of G
then π = 1UG for a subgroup U of G that intersects N trivially,
so π contains a constituent 1UNG of degree π(1) / |N|,
which can be viewed as a multiplicity-free permutation character of the
factor group G / N.
Moreover, no constituent of the difference π− 1UNG has N in its
kernel.
So if we know all multiplicity-free permutation characters of the factor group
G / N then we can compute all candidates for multiplicity-free permutation
characters of G by "filling up" each such character
[π] with a linear combination of characters not containing N
in their kernels, of total degree (|N|−1) ·π(1), and such that the
sum is a possible permutation character of G.
For this situation, GAP provides a special variant of the function
PermChars.
In a second step, the candidates are inspected whether the required point
stabilizers (and if yes, how many conjugacy classes of them) exist.
Finally, the permutation characters are verified by explicit induction from
the character tables of the point stabilizers.
The multiplicity-free permutation actions of the sporadic simple groups
and their automorphism groups are known by [BL96],
so this approach is suitable for these groups.
For central extensions of sporadic simple groups, the multiplicity-free
permutation characters have been classified in [LM];
this note describes a slightly different approach,
so we will give an independent confirmation of their results
(except for the error pointed out in Section 3.32).
First we load the Character Table Library [Bre25]
of the GAP system [GAP24],
and the GAP interface (see [WPN+22]) to the
ATLAS of Group Representations (see [WWT+]).
gap> LoadPackage( "ctbllib", false );
true
gap> LoadPackage( "atlasrep", false );
true
Then we read -if necessary- the file with GAP functions for computing
multiplicity-free permutation characters, and the file with the data.
Note that this includes the data we are going to compute,
but we will actually use only the data for sporadic simple groups and
their automorphism groups.
For the other groups, we will compare the results computed below with the
database.
gap> if not IsBound( PossiblePermutationCharactersWithBoundedMultiplicity )
> then
> ReadPackage( "ctbllib", "tst/multfree.g" );
> fi;
gap> if not IsBound( MultFreeEndoRingCharacterTables ) then
> ReadPackage( "ctbllib", "tst/mferctbl.gap" );
---------------------------------------------------------------------------
Loading the database of character tables of endomorphism rings of
multiplicity-free permutation modules of the sporadic simple groups and
their cyclic and bicyclic extensions, compiled by T. Breuer and J. Mueller.
---------------------------------------------------------------------------
> fi;
gap> if not IsBound( PossiblePermutationCharactersWithBoundedMultiplicity ) or
> not IsBound( MultFreeEndoRingCharacterTables ) then
> Print( "Sorry, the data files are not available!\n" );
> fi;
(If the data files are not available then they can be fetched from the
homepage of the GAP Character Table Library [Bre25].)
2.1 Computing Possible Permutation Characters
Next we define the GAP functions that are needed in the following.
The utility function PossiblePermutationCharacters
takes two ordinary character tables sub and tbl,
and returns the set of all induced class functions of the trivial character
of sub to tbl, w.r.t. the possible class fusions from sub to tbl.
(The entries in the result list are not necessarily multiplicity-free.)
gap> PossiblePermutationCharacters:= function( sub, tbl )
> local fus, triv;
>
> fus:= PossibleClassFusions( sub, tbl );
> if fus = fail then
> return fail;
> fi;
> triv:= [ TrivialCharacter( sub ) ];
>
> return Set( List( fus, map -> Induced( sub, tbl, triv, map )[1] ) );
> end;;
FaithfulCandidates takes the character table tbl of a group G
and the name factname of a factor group F of G for which the
multiplicity-free permutation characters are known,
and returns a list of lists, the entry at the i-th position being
the list of possible permutation characters of G that are multiplicity-free
and such that the sum of all constituents that are characters of F is the
i-th multiplicity-free permutation character of F.
As a side-effect, if the i-th entry is nonempty then information is printed
about the structure of the point-stabilizer in F and the number of
candidates found.
gap> FaithfulCandidates:= function( tbl, factname )
> local factinfo, factchars, facttbl, fus, sizeN, faith, i;
>
> # Fetch the data for the factor group.
> factinfo:= MultFreeEndoRingCharacterTables( factname );
> factchars:= List( factinfo, x -> x.character );
> facttbl:= UnderlyingCharacterTable( factchars[1] );
> fus:= GetFusionMap( tbl, facttbl );
> sizeN:= Size( tbl ) / Size( facttbl );
>
> # Compute faithful possible permutation characters.
> faith:= List( factchars, pi -> PermChars( tbl,
> rec( torso:= [ sizeN * pi[1] ],
> normalsubgroup:= ClassPositionsOfKernel( fus ),
> nonfaithful:= pi{ fus } ) ) );
>
> # Take only the multiplicity-free ones.
> faith:= List( faith, x -> Filtered( x, pi -> ForAll( Irr( tbl ),
> chi -> ScalarProduct( tbl, pi, chi ) < 2 ) ) );
>
> # Print info about the candidates.
> for i in [ 1 .. Length( faith ) ] do
> if not IsEmpty( faith[i] ) then
> Print( i, ": subgroup ", factinfo[i].subgroup,
> ", degree ", faith[i][1][1],
> " (", Length( faith[i] ), " cand.)\n" );
> fi;
> od;
>
> # Return the candidates.
> return faith;
> end;;
2.2 Verifying the Candidates
In the verification step, we check which of the given candidates of G
are induced from a given subgroup S.
For that, we use the following function.
Its arguments are the character table s of S,
the character tables tbl2 and tbl of G and its derived subgroup
G′ of index 2
(if G is perfect then 0 must be entered for tbl2),
the list candidates of characters of G,
and one of the strings "all", "extending", which means that we consider
either all possible class fusions of s into tbl2 or only those whose
image does not lie in G′.
Note that the table of the derived subgroup of G is needed because
we want to express the decomposition of the permutation characters
relative to G′.
The idea is that we know that n different permutation characters arise
from subgroups isomorphic with S (with the additional property that the
image of the embedding of S into G is not contained in G′
if the last argument is "extending"), and that candidates is a set
of possible permutation characters, of length n.
If the possible fusions between the character tables s and tbl2
lead to exactly the given n permutation characters then we have proved
that they are in fact the permutation characters of G in question.
In this case, VerifyCandidates prints information about the decomposition
of the permutation characters.
If none of candidates arises from the possible embeddings of S into G
then the function prints that S does not occur.
In all other cases, the function signals an error.
(This will not happen in the calls to this function below).
gap> VerifyCandidates:= function( s, tbl, tbl2, candidates, admissible )
> local fus, der, pi;
>
> if tbl2 = 0 then
> tbl2:= tbl;
> fi;
>
> # Compute the possible class fusions, and induce the trivial character.
> fus:= PossibleClassFusions( s, tbl2 );
> if admissible = "extending" then
> der:= Set( GetFusionMap( tbl, tbl2 ) );
> fus:= Filtered( fus, map -> not IsSubset( der, map ) );
> fi;
> pi:= Set( List( fus, map -> Induced( s, tbl2,
> [ TrivialCharacter( s ) ], map )[1] ) );
>
> # Compare the two lists.
> if pi = SortedList( candidates ) then
> Print( "G = ", Identifier( tbl2 ), ": point stabilizer ",
> Identifier( s ), ", ranks ",
> List( pi, x -> Length( ConstituentsOfCharacter(x) ) ), "\n" );
> if Size( tbl ) = Size( tbl2 ) then
> Print( PermCharInfo( tbl, pi ).ATLAS, "\n" );
> else
> Print( PermCharInfoRelative( tbl, tbl2, pi ).ATLAS, "\n" );
> fi;
> elif IsEmpty( Intersection( pi, candidates ) ) then
> Print( "G = ", Identifier( tbl2 ), ": no ", Identifier( s ), "\n" );
> else
> Error( "problem with verify" );
> fi;
> end;;
Since in most cases the character tables of possible point stabilizers
are contained in the GAP Character Table Library,
the above function provides an easy test.
Alternatively, we could compute all faithful possible permutation
characters (not only the multiplicity-free ones)
of the degree in question;
if there are as many different such characters as are known to be induced
from point stabilizers and if no other subgroups of this index
exist then the characters are indeed permutation characters,
and we can compare them with the multiplicity-free characters computed
before.
In the verification of the candidates, the following situations occur.
Lemma 1
Let Φ:[^G] → G be a group epimorphism,
with K = ker(Φ) cyclic of order m,
and let H be a subgroup of G such that m is coprime to the order
of the commutator factor group of H.
Assume that it is known that Φ−1(H) is a direct product of H
with K.
(This holds for example if H is simple and the order of the Schur
multiplier of H is coprime to m.)
Then the preimages under Φ of the G-conjugates of H
contain one [^G]-class of subgroups
that are isomorphic with H and that intersect trivially with K.
Lemma 2
Let Φ:[^G] → G be a group epimorphism,
with K = ker(Φ) of order 3, such that the derived subgroup
G′ of G has index 2 in G
and such that K is not central in [^G].
(So Φ−1(G′) is the centralizer of K in [^G].)
Consider a subgroup H of G with a subgroup H0 = H ∩G′
of index 2 in H, and assume that the preimage
Φ−1(H0) is a direct product of H0 with K.
(This holds for example if H0 is simple and the order of the Schur
multiplier of H0 is coprime to 3.)
Then each complement of K in Φ−1(H0)
extends in Φ−1(H) to exactly three complements of K
that are isomorphic with H and conjugate in Φ−1(H).
Lemma 3
Let Φ:[^G] → G be a group epimorphism,
with K = ker(Φ) of order 2.
Consider a subgroup H of G, with derived subgroup H′
of index 2 in H and such that
Φ−1(H′) is a direct product K ×H′.
(i)
Suppose that there is an element h ∈ H \H′
such that the squares of the preimages of h in [^G] lie in
the unique subgroup of index 2 in Φ−1(H′).
(This holds for example if the preimages of h are involutions.)
Then Φ−1(H) has the type K ×H.
(ii)
If Φ−1(H) has the type K ×H then
this group contains exactly two subgroups that are isomorphic with H.
If H is a maximal subgroup of G then these two subgroups are not
conjugate in [^G].
(iii)
Suppose that case (ii) applies and that there is
h ∈ H \H′ whose two preimages under Φ
are not conjugate in [^G]
and such that each of the two subgroups of the type H in
Φ−1(H) contains elements in only one conjugacy class of [^G]
that contain the preimages of h.
Then the two subgroups of the type H induce different permutation
characters of [^G], in particular exactly two conjugacy classes of
subgroups of the type H in [^G] arise from the conjugates of H
in G.
With character theoretic methods, we can check a weaker form of
Lemma 2.3 (i).
Namely, the conditions are clearly satisfied if there is a conjugacy class
C of elements in H that is not contained in H′
and such that the class of [^G] that
contains the squares of the preimages of C is not contained
in the images of the classes of 2 ×H′ that lie outside
H′.
The function CheckConditionsForLemma3 tests this, and prints a message
if Lemma 2.3 (i) applies because of this situation.
More precisely, the arguments are (in this order) the character tables of
H′, H, G, [^G], and one of the strings "all",
"extending"; the last argument expresses that either all embeddings of H
into G are considered or only those which do not lie inside the
derived subgroup of G.
The function assumes that s0 is the character table of the derived
subgroup of the group of s,
and that H′ lifts to a direct product in [^G].
gap> CheckConditionsForLemma3:= function( s0, s, fact, tbl, admissible )
> local s0fuss, poss, der, sfusfact, outerins, outerinfact, preim,
> squares, dp, dpfustbl, s0indp, other, goodclasses;
>
> if Size( s ) <> 2 * Size( s0 ) then
> Error( "<s> must be twice as large as <s0>" );
> fi;
>
> s0fuss:= GetFusionMap( s0, s );
> if s0fuss = fail then
> poss:= Set( List( PossiblePermutationCharacters( s0, s ),
> pi -> Filtered( [ 1 .. Length( pi ) ],
> i -> pi[i] <> 0 ) ) );
> if Length( poss ) = 1 then
> s0fuss:= poss[1];
> else
> Error( "classes of <s0> in <s> not determined" );
> fi;
> fi;
> sfusfact:= PossibleClassFusions( s, fact );
> if admissible = "extending" then
> der:= ClassPositionsOfDerivedSubgroup( fact );
> sfusfact:= Filtered( sfusfact, map -> not IsSubset( der, map ) );
> fi;
> outerins:= Difference( [ 1 .. NrConjugacyClasses( s ) ], s0fuss );
> outerinfact:= Set( List( sfusfact, map -> Set( map{ outerins } ) ) );
> if Length( outerinfact ) <> 1 then
> Error( "classes of `", s, "' inside `", fact, "' not determined" );
> fi;
>
> preim:= Flat( InverseMap( GetFusionMap( tbl, fact ) ){ outerinfact[1] } );
> squares:= Set( PowerMap( tbl, 2 ){ preim } );
> dp:= s0 * CharacterTable( "Cyclic", 2 );
> dpfustbl:= PossibleClassFusions( dp, tbl );
> s0indp:= GetFusionMap( s0, dp );
> other:= Difference( [ 1 .. NrConjugacyClasses( dp ) ], s0indp );
> goodclasses:= List( dpfustbl, map -> Intersection( squares,
> Difference( map{ s0indp }, map{ other } ) ) );
> if not IsEmpty( Intersection( goodclasses ) ) then
> Print( Identifier( tbl ), ": ", Identifier( s ),
> " lifts to a direct product,\n",
> "proved by squares in ", Intersection( goodclasses ), ".\n" );
> elif ForAll( goodclasses, IsEmpty ) then
> Print( Identifier( tbl ), ": ", Identifier( s ),
> " lifts to a nonsplit extension.\n" );
> else
> Print( "sorry, no proof of the splitting!\n" );
> fi;
> end;;
Lemma 2.3 (iii) can be utilized as follows.
We assume the situation of Lemma 2.3,
so Φ−1(H) is a direct product
〈z 〉×H, where z is an involution.
The derived subgroup of Φ−1(H) is H0 ≅ H′,
and Φ−1(H) contains two subgroups H1, H2
which are isomorphic with H,
and such that H2 = H0 ∪{ h z; h ∈ H1 \H0 }.
If the embedding of H1, say, into [^G] has the properties
that an element outside H0 is mapped into a class C of [^G]
that is different from z C and such that no element of H1 lies in z C
then z C contains elements of H2 but C does not.
In particular, the permutation characters of the two actions of [^G]
on the cosets of H1 and H2, respectively, are necessarily different.
We check this with the following function.
Its arguments are one class fusion from the character table of H1 to that
of [^G], the factor fusion from the character table of [^G] to
that of G,
and the list of positions of the classes of H0 in the character table
of H1.
The return value is true if there are two different permutation characters,
and false if this cannot be proved using the criterion.
gap> NecessarilyDifferentPermChars:= function( fusion, factfus, inner )
> local outer, inv;
>
> outer:= Difference( [ 1 .. Length( fusion ) ], inner );
> fusion:= fusion{ outer };
> inv:= Filtered( InverseMap( factfus ), IsList );
> return ForAny( inv, pair -> Length( Intersection( pair, fusion ) ) = 1 );
> end;;
The following observation is used to determine the number of conjugacy classes
of certain subgroups.
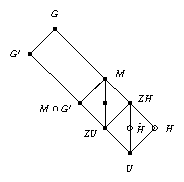
Lemma 4
Let G be a group with [G:G′] = 2,
and Z ⊆ Z(G) < G′ with |Z| = 2.
Consider a maximal subgroup M of G with Z < M and
M ⊄ eq G′,
and a subgroup H < M with [M:H] = 4
such that U = H ∩G′ is normal in M, U ≠ H holds,
and Z ⊄ eq H.
Let N = Z H.
Then the three subgroups of index two in N that lie above U are
Z U, H, and a group [H\tilde], say.
If M/U is a dihedral group of order eight
then the groups H and [H\tilde] are conjugate in M,
and M/U is a dihedral group of order eight if and only if
M \H contains both elements whose squares lie in U
and elements whose squares do not lie in U.
 We want to detect that M/U is a dihedral group by character theoretic
means but without using the character table of M.
A sufficient (but not necessary) condition is that the set
D = { g ∈ G | 1MG ≠ 0, 1NG(g) = 0 } is nonempty
and that there are elements g1, g2 ∈ D
with the properties 1UG(g12) = 0 and |g2| = 2.
The following function takes the character table of G and the
three permutation characters 1UG, 1MG, 1NG,
and returns a list of length two,
the i-th entry being the list of class positions of elements that can
serve as gi.
So M/U is proved to be a dihedral group if both entries are nonempty.
We want to detect that M/U is a dihedral group by character theoretic
means but without using the character table of M.
A sufficient (but not necessary) condition is that the set
D = { g ∈ G | 1MG ≠ 0, 1NG(g) = 0 } is nonempty
and that there are elements g1, g2 ∈ D
with the properties 1UG(g12) = 0 and |g2| = 2.
The following function takes the character table of G and the
three permutation characters 1UG, 1MG, 1NG,
and returns a list of length two,
the i-th entry being the list of class positions of elements that can
serve as gi.
So M/U is proved to be a dihedral group if both entries are nonempty.
gap> ProofOfD8Factor:= function( tblG, piU, piM, piN )
> local D, map, D1, D2;
>
> D:= Filtered( [ 1 .. Length( piU ) ], i -> piM[i] <> 0 and piN[i] = 0 );
> map:= PowerMap( tblG, 2 );
> D1:= Filtered( D, i -> piU[ map[i] ] = 0 );
> D2:= Filtered( D, i -> OrdersClassRepresentatives( tblG )[i] = 2 );
> return [ D1, D2 ];
> end;;
2.3 Isoclinic Groups
For dealing with the character tables of groups of the type 2.G.2 that are
isoclinic to those whose tables are printed in the ATLAS ([CCN+85]),
it is necessary to store explicitly the factor fusion from 2.G.2 onto G.2
and the subgroup fusion from 2.G into 2.G.2,
in order to make the above functions work.
Note that these maps coincide for the two isoclinism types.
gap> IsoclinicTable:= function( tbl, tbl2, facttbl )
> local subfus, factfus;
>
> subfus:= GetFusionMap( tbl, tbl2 );
> factfus:= GetFusionMap( tbl2, facttbl );
> tbl2:= CharacterTableIsoclinic( tbl2 );
> StoreFusion( tbl, subfus, tbl2 );
> StoreFusion( tbl2, factfus, facttbl );
> return tbl2;
> end;;
2.4 Tests for GAP
With the following function, we check whether the characters computed here
coincide with the characters stored in the data file.
gap> CompareWithDatabase:= function( name, chars )
> local info;
>
> info:= MultFreeEndoRingCharacterTables( name );
> info:= List( info, x -> x.character );;
> if SortedList( info ) <> SortedList( Concatenation( chars ) ) then
> Error( "contradiction 1 for ", name );
> fi;
> end;;
If the character tables of all maximal subgroups of G are known then
we could use alternatively the same method (and in fact the same GAP
functions) as in the classification in [BL96].
This is shown in the following sections where applicable,
using the following function.
(The function PossiblePermutationCharactersWithBoundedMultiplicity
is defined in the file tst/multfree.g of the
GAP Character Table Library [Bre25];
note that it returns not only faithful characters.)
gap> CompareWithCandidatesByMaxes:= function( name, faith )
> local tbl, poss;
>
> tbl:= CharacterTable( name );
> if not HasMaxes( tbl ) then
> Error( "no maxes stored for ", name );
> fi;
> poss:= PossiblePermutationCharactersWithBoundedMultiplicity( tbl, 1 );
> poss:= List( poss.permcand, l -> Filtered( l,
> pi -> ClassPositionsOfKernel( pi ) = [ 1 ] ) );
> if SortedList( Concatenation( poss ) )
> <> SortedList( Concatenation( faith ) ) then
> Error( "contradiction 2 for ", name );
> fi;
> end;;
3 The Groups
In the following,
we use ATLAS notation (see [CCN+85]) for the names of the groups.
In particular, 2 ×G and G ×2 denote the direct product
of the group G with a cyclic group of order 2,
and G.2 and 2.G denote an upward and downward extension, respectively,
of G by a cyclic group of order 2, such that these groups are not
direct products.
For groups of the structure 2.G.2 where the character table of G is
contained in the ATLAS, we use the name 2.G.2 for the isoclinism type
whose character table is printed in the ATLAS,
and (2.G.2)∗ for the other isoclinism type.
Most of the computations that are shown in the following use only information
from the GAP Character Table Library.
The (few) explicit computations with groups are collected in
Section 4.
3.1 G = 2.M12
The group 2.M12 has ten faithful multiplicity-free permutation actions,
with point stabilizers of the types M11 (twice),
A6.21 (twice), 32.2.S4 (four classes), and 32:2.A4 (twice).
gap> tbl:= CharacterTable( "2.M12" );;
gap> faith:= FaithfulCandidates( tbl, "M12" );;
1: subgroup $M_{11}$, degree 24 (1 cand.)
2: subgroup $M_{11}$, degree 24 (1 cand.)
5: subgroup $A_6.2_1 \leq A_6.2^2$, degree 264 (1 cand.)
8: subgroup $A_6.2_1 \leq A_6.2^2$, degree 264 (1 cand.)
11: subgroup $3^2.2.S_4$, degree 440 (2 cand.)
12: subgroup $3^2:2.A_4 \leq 3^2.2.S_4$, degree 880 (1 cand.)
13: subgroup $3^2.2.S_4$, degree 440 (2 cand.)
14: subgroup $3^2:2.A_4 \leq 3^2.2.S_4$, degree 880 (1 cand.)
There are two classes of M11 subgroups in M12 as well as in
2.M12, so we apply Lemma 2.1.
gap> VerifyCandidates( CharacterTable( "M11" ), tbl, 0,
> Concatenation( faith[1], faith[2] ), "all" );
G = 2.M12: point stabilizer M11, ranks [ 3, 3 ]
[ "1a+11a+12a", "1a+11b+12a" ]
According to the list of maximal subgroups of 2.M12,
any A6.22 subgroup in M12 lifts to a group of the structure
A6.D8 in M12, which contains two conjugate subgroups of the type
A6.21; so we get two classes of such subgroups, with the same permutation
character.
gap> Maxes( tbl );
[ "2xM11", "2.M12M2", "A6.D8", "2.M12M4", "2.L2(11)", "2x3^2.2.S4",
"2.M12M7", "2.M12M8", "2.M12M9", "2.M12M10", "2.A4xS3" ]
gap> faith[5] = faith[8];
true
gap> VerifyCandidates( CharacterTable( "A6.2_1" ), tbl, 0, faith[5], "all" );
G = 2.M12: point stabilizer A6.2_1, ranks [ 7 ]
[ "1a+11ab+12a+54a+55a+120b" ]
The 32.2.S4 type subgroups of M12 lift to direct products with
the centre of 2.M12, each such group contains two subgroups of the type
32.2.S4 which induce different permutation characters,
for example because the involutions in 32.2.S4 \32.2.A4
lie in the two preimages of the class 2B of M12.
gap> s:= CharacterTable( "3^2.2.S4" );;
gap> derpos:= ClassPositionsOfDerivedSubgroup( s );;
gap> facttbl:= CharacterTable( "M12" );;
gap> factfus:= GetFusionMap( tbl, facttbl );;
gap> ForAll( PossibleClassFusions( s, tbl ),
> map -> NecessarilyDifferentPermChars( map, factfus, derpos ) );
true
gap> VerifyCandidates( s, tbl, 0, Concatenation( faith[11], faith[13] ), "all" );
G = 2.M12: point stabilizer 3^2.2.S4, ranks [ 7, 7, 9, 9 ]
[ "1a+11a+54a+55a+99a+110ab", "1a+11b+54a+55a+99a+110ab",
"1a+11a+12a+44ab+54a+55a+99a+120b", "1a+11b+12a+44ab+54a+55a+99a+120b" ]
Each 32.2.S4 type group contains a unique subgroup of the type
32.2.A4, we get two classes of such subgroups, with
different permutation characters because already the corresponding characters
for M12 are different; we verify the candidates by inducing the degree
two permutation characters of the 32.2.S4 type groups to 2.M12.
gap> fus:= PossibleClassFusions( s, tbl );;
gap> deg2:= PermChars( s, 2 );
[ Character( CharacterTable( "3^2.2.S4" ),
[ 2, 2, 2, 2, 2, 2, 2, 0, 0, 0, 0 ] ) ]
gap> pi:= Set( List( fus, map -> Induced( s, tbl, deg2, map )[1] ) );;
gap> pi = SortedList( Concatenation( faith[12], faith[14] ) );
true
gap> PermCharInfo( tbl, pi ).ATLAS;
[ "1a+11a+12a+44ab+45a+54a+55ac+99a+110ab+120ab",
"1a+11b+12a+44ab+45a+54a+55ab+99a+110ab+120ab" ]
gap> CompareWithDatabase( "2.M12", faith );
gap> CompareWithCandidatesByMaxes( "2.M12", faith );
3.2 G = 2.M12.2
The group 2.M12.2 that is printed in the ATLAS has three faithful
multiplicity-free permutation actions,
with point stabilizers of the types M11 and L2(11).2 (twice),
respectively.
gap> tbl2:= CharacterTable( "2.M12.2" );;
gap> faith:= FaithfulCandidates( tbl2, "M12.2" );;
1: subgroup $M_{11}$, degree 48 (1 cand.)
2: subgroup $L_2(11).2$, degree 288 (2 cand.)
The two classes of subgroups of the type M11 in 2.M12 are fused in
2.M12.2, so we get one class of these subgroups.
gap> VerifyCandidates( CharacterTable( "M11" ), tbl, tbl2, faith[1], "all" );
G = 2.M12.2: point stabilizer M11, ranks [ 5 ]
[ "1a^{\\pm}+11ab+12a^{\\pm}" ]
The outer involutions in the maximal subgroups of the type L2(11).2
in M12.2 lift to involutions in 2.M12.2;
moreover, those subgroups of the type L2(11).2 that are novelties
(so the intersection with M12 lies in M11 type subgroups)
contain 2B elements, which lift to involutions in 2.M12.2,
so the L2(11) subgroup lifts to a group of the type 2 ×L2(11),
and Lemma 2.3 (ii) yields two classes of subgroups.
The permutation characters are different, for example because
each of the two candidates contains elements in one of the
two preimages of the class 2B.
(The function CheckConditionsForLemma3 fails here,
because of the two classes of maximal subgroups L2(11).2 in M12.2.
One of them contains 2A elements, the other contains 2B elements.
Only the latter type of subgroups, whose intersection with M12 is not
maximal in M12, lifts to subgroups of 2.M12.2 that contain
L2(11).2 subgroups.)
gap> s:= CharacterTable( "L2(11).2" );;
gap> derpos:= ClassPositionsOfDerivedSubgroup( s );;
gap> facttbl:= CharacterTable( "M12.2" );;
gap> factfus:= GetFusionMap( tbl2, facttbl );;
gap> ForAll( PossibleClassFusions( s, tbl2 ),
> map -> NecessarilyDifferentPermChars( map, factfus, derpos ) );
true
gap> VerifyCandidates( s, tbl, tbl2, faith[2], "all" );
G = 2.M12.2: point stabilizer L2(11).2, ranks [ 7, 7 ]
[ "1a^++11ab+12a^{\\pm}+55a^++66a^++120b^-",
"1a^++11ab+12a^{\\pm}+55a^++66a^++120b^+" ]
gap> CompareWithDatabase( "2.M12.2", faith );
The group (2.M12.2)∗ of the isoclinism type that is not printed
in the ATLAS has one faithful multiplicity-free permutation action,
with point stabilizer of the type M11;
as this subgroup lies inside 2.M12, its existence is clear,
and the permutation character in both groups of the type 2.M12.2
is the same.
gap> tbl2:= IsoclinicTable( tbl, tbl2, facttbl );;
gap> faith:= FaithfulCandidates( tbl2, "M12.2" );;
1: subgroup $M_{11}$, degree 48 (1 cand.)
gap> CompareWithDatabase( "Isoclinic(2.M12.2)", faith );
Note that in (2.M12.2)∗,
the subgroup of the type (2 ×L2(11)).2 is a nonsplit extension,
so the unique index 2 subgroup in this group contains the centre of
2.M12.2, in particular there is no subgroup of the type L2(11).2.
gap> PossibleClassFusions( CharacterTable( "L2(11).2" ), tbl2 );
[ ]
3.3 G = 2.M22
The group 2.M22 has four faithful multiplicity-free permutation actions,
with point stabilizers of the types 24:A5, A7 (twice),
and 23:L3(2), by Lemma 2.1.
gap> tbl:= CharacterTable( "2.M22" );;
gap> faith:= FaithfulCandidates( tbl, "M22" );;
3: subgroup $2^4:A_5 \leq 2^4:A_6$, degree 924 (1 cand.)
4: subgroup $A_7$, degree 352 (1 cand.)
5: subgroup $A_7$, degree 352 (1 cand.)
7: subgroup $2^3:L_3(2)$, degree 660 (1 cand.)
Note that one class of subgroups of the type 24:A5 in the maximal subgroup
of the type 24:A6 as well as the A7 and 23:L3(2) subgroups
lift to direct products in 2.M22.
A proof for 24:A5 using explicit computations with the group can be found
in Section 4.1.
gap> Maxes( tbl );
[ "2.L3(4)", "2.M22M2", "2xA7", "2xA7", "2.M22M5", "2x2^3:L3(2)",
"(2xA6).2_3", "2xL2(11)" ]
gap> s:= CharacterTable( "P1/G1/L1/V1/ext2" );;
gap> VerifyCandidates( s, tbl, 0, faith[3], "all" );
G = 2.M22: point stabilizer P1/G1/L1/V1/ext2, ranks [ 8 ]
[ "1a+21a+55a+126ab+154a+210b+231a" ]
gap> faith[4] = faith[5];
true
gap> VerifyCandidates( CharacterTable( "A7" ), tbl, 0, faith[4], "all" );
G = 2.M22: point stabilizer A7, ranks [ 5 ]
[ "1a+21a+56a+120a+154a" ]
gap> VerifyCandidates( CharacterTable( "M22M6" ), tbl, 0, faith[7], "all" );
G = 2.M22: point stabilizer 2^3:sl(3,2), ranks [ 7 ]
[ "1a+21a+55a+99a+120a+154a+210b" ]
gap> CompareWithDatabase( "2.M22", faith );
gap> CompareWithCandidatesByMaxes( "2.M22", faith );
3.4 G = 2.M22.2
The group 2.M22.2 that is printed in the ATLAS has eight faithful
multiplicity-free permutation actions,
with point stabilizers of the types 24:S5 (twice), A7,
23:L3(2) ×2 (twice), 23:L3(2), and L2(11).2 (twice).
gap> tbl2:= CharacterTable( "2.M22.2" );;
gap> faith:= FaithfulCandidates( tbl2, "M22.2" );;
6: subgroup $2^4:S_5 \leq 2^4:S_6$, degree 924 (2 cand.)
7: subgroup $A_7$, degree 704 (1 cand.)
11: subgroup $2^3:L_3(2) \times 2$, degree 660 (2 cand.)
12: subgroup $2^3:L_3(2) \leq 2^3:L_3(2) \times 2$, degree 1320 (2 cand.)
16: subgroup $L_2(11).2$, degree 1344 (2 cand.)
The character table of the 24:S5 type subgroup is contained in the GAP
Character Table Library,
with identifier w(d5) (which denotes the Weyl group of the type D5,
cf. Section 4.2).
gap> s:= CharacterTable( "w(d5)" );;
gap> derpos:= ClassPositionsOfDerivedSubgroup( s );;
gap> facttbl:= CharacterTable( "M22.2" );;
gap> factfus:= GetFusionMap( tbl2, facttbl );;
gap> ForAll( PossibleClassFusions( s, tbl2 ),
> map -> NecessarilyDifferentPermChars( map, factfus, derpos ) );
true
gap> VerifyCandidates( s, tbl, tbl2, faith[6], "all" );
G = 2.M22.2: point stabilizer w(d5), ranks [ 7, 7 ]
[ "1a^++21a^++55a^++126ab+154a^++210b^-+231a^-",
"1a^++21a^++55a^++126ab+154a^++210b^++231a^-" ]
The two classes of the type A7 subgroups in 2.M22 are fused
in 2.M22.2.
gap> VerifyCandidates( CharacterTable( "A7" ), tbl, tbl2, faith[7], "all" );
G = 2.M22.2: point stabilizer A7, ranks [ 10 ]
[ "1a^{\\pm}+21a^{\\pm}+56a^{\\pm}+120a^{\\pm}+154a^{\\pm}" ]
The preimages of the 23:L3(2) ×2 type subgroups of M22.2
in 2.M22.2 are direct products, by the discussion of 2.M22
and Lemma 2.3 (i).
So Lemma 2.3 (iii) yields two classes,
with different permutation characters.
gap> s:= CharacterTable( "2x2^3:L3(2)" );;
gap> s0:= CharacterTable( "2^3:sl(3,2)" );;
gap> CheckConditionsForLemma3( s0, s, facttbl, tbl2, "extending" );
2.M22.2: 2x2^3:L3(2) lifts to a direct product,
proved by squares in [ 1, 5, 14, 16 ].
gap> derpos:= ClassPositionsOfDerivedSubgroup( s );;
gap> ForAll( PossibleClassFusions( s, tbl2 ),
> map -> NecessarilyDifferentPermChars( map, factfus, derpos ) );
true
gap> VerifyCandidates( s, tbl, tbl2, faith[11], "extending" );
G = 2.M22.2: point stabilizer 2x2^3:L3(2), ranks [ 7, 7 ]
[ "1a^++21a^++55a^++99a^++120a^-+154a^++210b^-",
"1a^++21a^++55a^++99a^++120a^++154a^++210b^+" ]
There is one class of subgroups of the type 23:L3(2) in 2.M22.
One of the two candidates of degree 1 320 is excluded because it does not
arise from a possible class fusion.
gap> s:= CharacterTable( "M22M6" );;
gap> pi1320:= PossiblePermutationCharacters( s, tbl2 );;
gap> Length( pi1320 );
1
gap> IsSubset( faith[12], pi1320 );
true
gap> faith[12]:= pi1320;;
gap> VerifyCandidates( s, tbl, tbl2, faith[12], "all" );
G = 2.M22.2: point stabilizer 2^3:sl(3,2), ranks [ 14 ]
[ "1a^{\\pm}+21a^{\\pm}+55a^{\\pm}+99a^{\\pm}+120a^{\\pm}+154a^{\\pm}+210b^{\\\
pm}" ]
By Lemma 2.3 (i),
the preimages of the L2(11).2 type subgroups of M22.2 in 2.M22.2
are direct products,
so Lemma 2.3 (iii) yields two classes,
with different permutation characters.
gap> s:= CharacterTable( "L2(11).2" );;
gap> s0:= CharacterTable( "L2(11)" );;
gap> CheckConditionsForLemma3( s0, s, facttbl, tbl2, "all" );
2.M22.2: L2(11).2 lifts to a direct product,
proved by squares in [ 1, 4, 10, 13 ].
gap> derpos:= ClassPositionsOfDerivedSubgroup( s );;
gap> ForAll( PossibleClassFusions( s, tbl2 ),
> map -> NecessarilyDifferentPermChars( map, factfus, derpos ) );
true
gap> VerifyCandidates( CharacterTable( "L2(11).2" ), tbl, tbl2, faith[16], "all" );
G = 2.M22.2: point stabilizer L2(11).2, ranks [ 10, 10 ]
[ "1a^++21a^-+55a^++56a^{\\pm}+120a^-+154a^++210a^-+231a^-+440a^+",
"1a^++21a^-+55a^++56a^{\\pm}+120a^++154a^++210a^-+231a^-+440a^-" ]
gap> CompareWithDatabase( "2.M22.2", faith );
The group (2.M22.2)∗ of the isoclinism type that is not printed
in the ATLAS has two faithful multiplicity-free permutation actions,
with point stabilizers of the types A7 and 23:L3(2).
gap> tbl2:= IsoclinicTable( tbl, tbl2, facttbl );;
gap> faith:= FaithfulCandidates( tbl2, "M22.2" );;
7: subgroup $A_7$, degree 704 (1 cand.)
12: subgroup $2^3:L_3(2) \leq 2^3:L_3(2) \times 2$, degree 1320 (2 cand.)
gap> faith[12]:= Filtered( faith[12], chi -> chi in pi1320 );;
gap> CompareWithDatabase( "Isoclinic(2.M22.2)", faith );
The two classes of subgroups lie inside 2.M22,
so their existence has been discussed already above.
3.5 G = 3.M22
The group 3.M22 has four faithful multiplicity-free permutation actions,
with point stabilizers of the types 24:A5, 24:S5, 23:L3(2),
and L2(11).
gap> tbl:= CharacterTable( "3.M22" );;
gap> faith:= FaithfulCandidates( tbl, "M22" );;
3: subgroup $2^4:A_5 \leq 2^4:A_6$, degree 1386 (1 cand.)
6: subgroup $2^4:S_5$, degree 693 (1 cand.)
7: subgroup $2^3:L_3(2)$, degree 990 (1 cand.)
9: subgroup $L_2(11)$, degree 2016 (1 cand.)
The existence of one class of each of these types follows from
Lemma 2.1.
gap> VerifyCandidates( CharacterTable( "P1/G1/L1/V1/ext2" ), tbl, 0, faith[3], "all" );
G = 3.M22: point stabilizer P1/G1/L1/V1/ext2, ranks [ 13 ]
[ "1a+21abc+55a+105abcd+154a+231abc" ]
gap> VerifyCandidates( CharacterTable( "M22M5" ), tbl, 0, faith[6], "all" );
G = 3.M22: point stabilizer 2^4:s5, ranks [ 10 ]
[ "1a+21abc+55a+105abcd+154a" ]
gap> VerifyCandidates( CharacterTable( "M22M6" ), tbl, 0, faith[7], "all" );
G = 3.M22: point stabilizer 2^3:sl(3,2), ranks [ 13 ]
[ "1a+21abc+55a+99abc+105abcd+154a" ]
gap> VerifyCandidates( CharacterTable( "M22M8" ), tbl, 0, faith[9], "all" );
G = 3.M22: point stabilizer L2(11), ranks [ 16 ]
[ "1a+21abc+55a+105abcd+154a+210abc+231abc" ]
gap> CompareWithDatabase( "3.M22", faith );
gap> CompareWithCandidatesByMaxes( "3.M22", faith );
3.6 G = 3.M22.2
The group 3.M22.2 has five faithful multiplicity-free permutation
actions, with point stabilizers of the types 24:S5, 25:S5,
24:(A5 ×2), 23:L3(2) ×2, and L2(11).2.
gap> tbl2:= CharacterTable( "3.M22.2" );;
gap> faith:= FaithfulCandidates( tbl2, "M22.2" );;
6: subgroup $2^4:S_5 \leq 2^4:S_6$, degree 1386 (1 cand.)
8: subgroup $2^5:S_5$, degree 693 (1 cand.)
10: subgroup $2^4:(A_5 \times 2) \leq 2^5:S_5$, degree 1386 (1 cand.)
11: subgroup $2^3:L_3(2) \times 2$, degree 990 (1 cand.)
16: subgroup $L_2(11).2$, degree 2016 (1 cand.)
Subgroups of these types exist by Lemma 2.2.
The verification is straightforward in all cases
except that of 24:(A5 ×2).
gap> VerifyCandidates( CharacterTable( "w(d5)" ), tbl, tbl2, faith[6], "all" );
G = 3.M22.2: point stabilizer w(d5), ranks [ 9 ]
[ "1a^++21a^+bc+55a^++105abcd+154a^++231a^-bc" ]
gap> VerifyCandidates( CharacterTable( "M22.2M4" ), tbl, tbl2, faith[8], "all" );
G = 3.M22.2: point stabilizer M22.2M4, ranks [ 7 ]
[ "1a^++21a^+bc+55a^++105abcd+154a^+" ]
gap> VerifyCandidates( CharacterTable( "2x2^3:L3(2)" ), tbl, tbl2, faith[11], "all" );
G = 3.M22.2: point stabilizer 2x2^3:L3(2), ranks [ 9 ]
[ "1a^++21a^+bc+55a^++99a^+bc+105abcd+154a^+" ]
gap> VerifyCandidates( CharacterTable( "L2(11).2" ), tbl, tbl2, faith[16], "all" );
G = 3.M22.2: point stabilizer L2(11).2, ranks [ 11 ]
[ "1a^++21a^-bc+55a^++105abcd+154a^++210a^-bc+231a^-bc" ]
In the remaining case, we note that the 24:(A5 ×2) type subgroup
has index 2 in the maximal subgroup of the type 25:S5,
whose character table is available via the identifier M22.2M4.
It is sufficient to show that exactly one of the three index 2
subgroups in this group induces a multiplicity-free permutation character
of 3.M22.2,
and this can be done by inducing the degree 2 permutation characters
of 25:S5 to 3.M22.2.
gap> s:= CharacterTable( "M22.2M4" );;
gap> lin:= LinearCharacters( s );
[ Character( CharacterTable( "M22.2M4" ),
[ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 ] )
, Character( CharacterTable( "M22.2M4" ),
[ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1 ] ), Character( CharacterTable( "M22.2M4" ),
[ 1, 1, 1, 1, 1, 1, 1, -1, -1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1, -1, -1, -1,
-1, -1 ] ), Character( CharacterTable( "M22.2M4" ),
[ 1, 1, 1, 1, 1, 1, 1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 1,
1, 1, 1, 1 ] ) ]
gap> perms:= List( lin{ [ 2 .. 4 ] }, chi -> chi + lin[1] );;
gap> sfustbl2:= PossibleClassFusions( s, tbl2 );;
gap> Length( sfustbl2 );
2
gap> ind1:= Induced( s, tbl2, perms, sfustbl2[1] );;
gap> ind2:= Induced( s, tbl2, perms, sfustbl2[2] );;
gap> PermCharInfo( tbl2, ind1 ).ATLAS;
[ "1ab+21ab+42aa+55ab+154ab+210ccdd", "1a+21ab+42a+55a+154a+210bcd+462a",
"1a+21aa+42a+55a+154a+210acd+462a" ]
gap> PermCharInfo( tbl2, ind2 ).ATLAS;
[ "1a+21aa+42a+55a+154a+210acd+462a", "1a+21ab+42a+55a+154a+210bcd+462a",
"1ab+21ab+42aa+55ab+154ab+210ccdd" ]
gap> ind1[2] = ind2[2];
true
gap> [ ind1[2] ] = faith[10];
true
gap> CompareWithDatabase( "3.M22.2", faith );
3.7 G = 4.M22 and G = 12.M22
The group 4.M22 and hence also the group 12.M22 has no
faithful multiplicity-free permutation action.
gap> tbl:= CharacterTable( "4.M22" );;
gap> faith:= FaithfulCandidates( tbl, "2.M22" );;
gap> CompareWithDatabase( "4.M22", faith );
gap> CompareWithCandidatesByMaxes( "4.M22", faith );
3.8 G = 4.M22.2 and G = 12.M22.2
The two isoclinism types of groups of the type 4.M22.2 and hence also all
groups of the type 12.M22.2 have no faithful multiplicity-free
permutation actions.
gap> tbl2:= CharacterTable( "4.M22.2" );;
gap> faith:= FaithfulCandidates( tbl2, "M22.2" );;
gap> CompareWithDatabase( "4.M22.2", faith );
gap> CompareWithDatabase( "12.M22.2", [] );
gap> tbl2:= IsoclinicTable( tbl, tbl2, facttbl );;
gap> faith:= FaithfulCandidates( tbl2, "M22.2" );;
gap> CompareWithDatabase( "Isoclinic(4.M22.2)", faith );
gap> CompareWithDatabase( "Isoclinic(12.M22.2)", [] );
3.9 G = 6.M22
The group 6.M22 has two faithful multiplicity-free permutation actions,
with point stabilizers of the types 24:A5 and 23:L3(2).
gap> tbl:= CharacterTable( "6.M22" );;
gap> faith:= FaithfulCandidates( tbl, "3.M22" );;
1: subgroup $2^4:A_5 \rightarrow (M_{22},3)$, degree 2772 (1 cand.)
3: subgroup $2^3:L_3(2) \rightarrow (M_{22},7)$, degree 1980 (1 cand.)
The existence of one class of each of these subgroups follows from the
treatment of 2.M22 and 3.M22.
gap> VerifyCandidates( CharacterTable( "P1/G1/L1/V1/ext2" ), tbl, 0, faith[1], "all" );
G = 6.M22: point stabilizer P1/G1/L1/V1/ext2, ranks [ 22 ]
[ "1a+21abc+55a+105abcd+126abcdef+154a+210bef+231abc" ]
gap> VerifyCandidates( CharacterTable( "M22M6" ), tbl, 0, faith[3], "all" );
G = 6.M22: point stabilizer 2^3:sl(3,2), ranks [ 17 ]
[ "1a+21abc+55a+99abc+105abcd+120a+154a+210b+330de" ]
gap> CompareWithDatabase( "6.M22", faith );
gap> CompareWithCandidatesByMaxes( "6.M22", faith );
3.10 G = 6.M22.2
The group 6.M22.2 that is printed in the ATLAS has six faithful
multiplicity-free permutation actions,
with point stabilizers of the types 24:S5 (twice),
23:L3(2) ×2 (twice), and L2(11).2 (twice).
gap> tbl2:= CharacterTable( "6.M22.2" );;
gap> faith:= FaithfulCandidates( tbl2, "M22.2" );;
6: subgroup $2^4:S_5 \leq 2^4:S_6$, degree 2772 (2 cand.)
11: subgroup $2^3:L_3(2) \times 2$, degree 1980 (2 cand.)
16: subgroup $L_2(11).2$, degree 4032 (2 cand.)
We know that 2.M22.2 contains two classes of subgroups isomorphic with
each of the required point stabilizers, so we apply Lemma 2.2.
gap> s:= CharacterTable( "w(d5)" );;
gap> VerifyCandidates( s, tbl, tbl2, faith[6], "all" );
G = 6.M22.2: point stabilizer w(d5), ranks [ 14, 14 ]
[ "1a^++21a^+bc+55a^++105abcd+126abcdef+154a^++210b^-ef+231a^-bc",
"1a^++21a^+bc+55a^++105abcd+126abcdef+154a^++210b^+ef+231a^-bc" ]
(Since 6.M22 contains subgroups of the type 23:L3(2) ×2
in which we are not interested,
we must use "extending" as the last argument of VerifyCandidates
for this case.)
gap> s:= CharacterTable( "2x2^3:L3(2)" );;
gap> VerifyCandidates( s, tbl, tbl2, faith[11], "extending" );
G = 6.M22.2: point stabilizer 2x2^3:L3(2), ranks [ 12, 12 ]
[ "1a^++21a^+bc+55a^++99a^+bc+105abcd+120a^-+154a^++210b^-+330de",
"1a^++21a^+bc+55a^++99a^+bc+105abcd+120a^++154a^++210b^++330de" ]
gap> VerifyCandidates( CharacterTable( "L2(11).2" ), tbl, tbl2, faith[16], "all" );
G = 6.M22.2: point stabilizer L2(11).2, ranks [ 20, 20 ]
[ "1a^++21a^-bc+55a^++56a^{\\pm}+66abcd+105abcd+120a^-bc+154a^++210a^-cdghij+2\
31a^-bc+440a^+",
"1a^++21a^-bc+55a^++56a^{\\pm}+66abcd+105abcd+120a^+bc+154a^++210a^-cdghij+2\
31a^-bc+440a^-" ]
gap> CompareWithDatabase( "6.M22.2", faith );
The group (6.M22.2)∗ of the isoclinism type that is not printed
in the ATLAS has no faithful multiplicity-free permutation action.
gap> tbl2:= IsoclinicTable( tbl, tbl2, facttbl );;
gap> faith:= FaithfulCandidates( tbl2, "M22.2" );;
gap> CompareWithDatabase( "Isoclinic(6.M22.2)", faith );
3.11 G = 2.J2
The group 2.J2 has one faithful multiplicity-free permutation action,
with point stabilizer of the type U3(3), by Lemma 2.1.
gap> tbl:= CharacterTable( "2.J2" );;
gap> faith:= FaithfulCandidates( tbl, "J2" );;
1: subgroup $U_3(3)$, degree 200 (1 cand.)
gap> VerifyCandidates( CharacterTable( "U3(3)" ), tbl, 0, faith[1], "all" );
G = 2.J2: point stabilizer U3(3), ranks [ 5 ]
[ "1a+36a+50ab+63a" ]
gap> CompareWithDatabase( "2.J2", faith );
gap> CompareWithCandidatesByMaxes( "2.J2", faith );
3.12 G = 2.J2.2
The group 2.J2.2 that is printed in the ATLAS has no faithful
multiplicity-free permutation action.
gap> tbl2:= CharacterTable( "2.J2.2" );;
gap> faith:= FaithfulCandidates( tbl2, "J2.2" );;
gap> CompareWithDatabase( "2.J2.2", faith );
The group (2.J2.2)∗ of the isoclinism type that is not printed
in the ATLAS has three faithful multiplicity-free permutation actions,
with point stabilizers of the types U3(3).2 (twice) and
3.A6.23.
gap> facttbl:= CharacterTable( "J2.2" );;
gap> tbl2:= IsoclinicTable( tbl, tbl2, facttbl );;
gap> faith:= FaithfulCandidates( tbl2, "J2.2" );;
1: subgroup $U_3(3).2$, degree 200 (1 cand.)
5: subgroup $3.A_6.2_3 \leq 3.A_6.2^2$, degree 1120 (1 cand.)
The existence of two classes of U3(3) type subgroups follows from
Lemma 2.3 (ii).
gap> s0:= CharacterTable( "U3(3)" );;
gap> s:= CharacterTable( "U3(3).2" );;
gap> CheckConditionsForLemma3( s0, s, facttbl, tbl2, "all" );
Isoclinic(2.J2.2): U3(3).2 lifts to a direct product,
proved by squares in [ 1, 3, 8, 16 ].
gap> VerifyCandidates( s, tbl, tbl2, faith[1], "all" );
G = Isoclinic(2.J2.2): point stabilizer U3(3).2, ranks [ 4 ]
[ "1a^++36a^++50ab+63a^+" ]
Each maximal subgroup of the type 3.A6.22 in J2.2 contains
a subgroup U of the type 3.A6.23, which lifts to a direct product
N = 2 ×3.A6.23 in (2.J2.2)∗.
gap> s0:= CharacterTable( "3.A6" );;
gap> s:= CharacterTable( "3.A6.2_3" );;
gap> CheckConditionsForLemma3( s0, s, facttbl, tbl2, "all" );
Isoclinic(2.J2.2): 3.A6.2_3 lifts to a direct product,
proved by squares in [ 3, 10, 16, 25 ].
There is only one class of 3.A6.23 type subgroups
in each maximal subgroup M of G = (2.J2.2)∗ that is a preimage
of a 3.A6.22 type subgroup in J2.2.
This follows from the fact that the normalizer of H = 3.A6.23 in G
is N;
equivalently, the factor group of M modulo U = H′
is a dihedral group of order 8.
With character-theoretic methods, this can be seen as follows.
gap> tblMbar:= CharacterTable( "3.A6.2^2" );;
gap> piMbar:= PossiblePermutationCharacters( tblMbar, facttbl );
[ Character( CharacterTable( "J2.2" ),
[ 280, 40, 12, 1, 4, 4, 10, 0, 1, 0, 0, 2, 2, 0, 1, 1, 14, 10, 0, 2, 4, 0,
1, 0, 0, 1, 1 ] ) ]
gap> piM:= piMbar[1]{ GetFusionMap( tbl2, facttbl ) };;
gap> piNbar:= PossiblePermutationCharacters( s, facttbl );
[ Character( CharacterTable( "J2.2" ),
[ 560, 80, 0, 2, 8, 8, 20, 0, 2, 0, 0, 0, 0, 0, 2, 2, 0, 8, 0, 0, 8, 0, 2,
0, 0, 2, 2 ] ) ]
gap> piN:= piNbar[1]{ GetFusionMap( tbl2, facttbl ) };;
gap> piU:= PossiblePermutationCharacters( s0, tbl2 );
[ Character( CharacterTable( "Isoclinic(2.J2.2)" ),
[ 2240, 0, 320, 0, 0, 8, 0, 32, 0, 32, 0, 80, 0, 0, 0, 8, 0, 0, 0, 0, 0, 0,
0, 0, 8, 0, 8, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
] ) ]
gap> ProofOfD8Factor( tbl2, piU[1], piM, piN );
[ [ 5, 21, 22 ], [ 29 ] ]
It remains to verify the candidate.
gap> VerifyCandidates( s, tbl, tbl2, faith[5], "all" );
G = Isoclinic(2.J2.2): point stabilizer 3.A6.2_3, ranks [ 12 ]
[ "1a^++14c^{\\pm}+21ab+50ab+63a^{\\pm}+90a^++126a^++175a^-+216a^{\\pm}" ]
gap> faith[1]:= faith[1]{ [ 1, 1 ] };;
gap> CompareWithDatabase( "Isoclinic(2.J2.2)", faith );
3.13 G = 2.HS
The group 2.HS has five faithful multiplicity-free permutation actions,
with point stabilizers of the types U3(5) (twice), A8,
and M11 (twice).
gap> tbl:= CharacterTable( "2.HS" );;
gap> faith:= FaithfulCandidates( tbl, "HS" );;
3: subgroup $U_3(5) \leq U_3(5).2$, degree 704 (1 cand.)
5: subgroup $U_3(5) \leq U_3(5).2$, degree 704 (1 cand.)
8: subgroup $A_8 \leq A_8.2$, degree 4400 (1 cand.)
10: subgroup $M_{11}$, degree 11200 (1 cand.)
11: subgroup $M_{11}$, degree 11200 (1 cand.)
Lemma 2.1 applies in all cases; note that 2.HS does not admit
an embedding of 2.A8.
gap> VerifyCandidates( CharacterTable( "U3(5)" ), tbl, 0,
> Concatenation( faith[3], faith[5] ), "all" );
G = 2.HS: point stabilizer U3(5), ranks [ 6, 6 ]
[ "1a+22a+154c+175a+176ab", "1a+22a+154b+175a+176ab" ]
gap> PossibleClassFusions( CharacterTable( "2.A8" ), tbl );
[ ]
gap> VerifyCandidates( CharacterTable( "A8" ), tbl, 0, faith[8], "all" );
G = 2.HS: point stabilizer A8, ranks [ 13 ]
[ "1a+22a+77a+154abc+175a+176ab+693a+770a+924ab" ]
gap> VerifyCandidates( CharacterTable( "M11" ), tbl, 0,
> Concatenation( faith[10], faith[11] ), "all" );
G = 2.HS: point stabilizer M11, ranks [ 16, 16 ]
[ "1a+22a+56a+77a+154c+175a+176ab+616ab+770a+825a+1056a+1980ab+2520a",
"1a+22a+56a+77a+154b+175a+176ab+616ab+770a+825a+1056a+1980ab+2520a" ]
gap> CompareWithDatabase( "2.HS", faith );
gap> CompareWithCandidatesByMaxes( "2.HS", faith );
3.14 G = 2.HS.2
The group 2.HS.2 that is printed in the ATLAS has two faithful
multiplicity-free permutation actions,
with point stabilizers of the types A8 ×2 and A8.2.
gap> tbl2:= CharacterTable( "2.HS.2" );;
gap> faith:= FaithfulCandidates( tbl2, "HS.2" );;
10: subgroup $A_8 \times 2 \leq A_8.2 \times 2$, degree 4400 (1 cand.)
11: subgroup $A_8.2 \leq A_8.2 \times 2$, degree 4400 (1 cand.)
The existence of subgroups for each candidate follows from
Lemma 2.3.
(Since there are A8 ×2 type subgroups inside 2.HS in which we are
not interested,
we must use "extending" as the last argument of VerifyCandidates.)
gap> facttbl:= CharacterTable( "HS.2" );;
gap> factfus:= GetFusionMap( tbl2, facttbl );;
gap> s0:= CharacterTable( "A8" );;
gap> s:= s0 * CharacterTable( "Cyclic", 2 );
CharacterTable( "A8xC2" )
gap> CheckConditionsForLemma3( s0, s, facttbl, tbl2, "all" );
2.HS.2: A8xC2 lifts to a direct product,
proved by squares in [ 1, 6, 13, 20, 30 ].
gap> VerifyCandidates( s, tbl, tbl2, faith[10], "extending" );
G = 2.HS.2: point stabilizer A8xC2, ranks [ 10 ]
[ "1a^++22a^++77a^++154a^+bc+175a^++176ab+693a^++770a^++924ab" ]
gap> s:= CharacterTable( "A8.2" );;
gap> CheckConditionsForLemma3( s0, s, facttbl, tbl2, "extending" );
2.HS.2: A8.2 lifts to a direct product,
proved by squares in [ 1, 6, 13 ].
gap> VerifyCandidates( s, tbl, tbl2, faith[11], "all" );
G = 2.HS.2: point stabilizer A8.2, ranks [ 10 ]
[ "1a^++22a^-+77a^++154a^+bc+175a^++176ab+693a^++770a^-+924ab" ]
gap> CompareWithDatabase( "2.HS.2", faith );
Note that any maximal S8 ×2 type subgroup in HS.2 contains two
subgroups of the type S8, and the one that is contained in HS
does not lift to a direct product in G = 2.HS.2
but to a subdirect product S of S8 and a cyclic group of order four,
since 2.HS does not contain S8 type subgroups.
Let M be a maximal subgroup of G that maps to a subgroup of the type
S8 ×2 in the factor group HS.2.
By the above observations, we know three subgroups of index two in M:
the subdirect product S and the direct products S8 ×2
and A8 ×22.
So we see that the factor group of M by the A8 type subgroup
is a dihedral group of order eight.
(The situation is similar to that in Section 3.12,
but the sufficient condition checked by the function ProofOfD8Factor
is not satisfied here, as the following computation shows.
We have U ≅ A8 and N ≅ A8 ×22.)
gap> tblMbar:= CharacterTable( "A8.2" ) * CharacterTable( "Cyclic", 2 );;
gap> piMbar:= PossiblePermutationCharacters( tblMbar, facttbl );
[ Character( CharacterTable( "HS.2" ),
[ 1100, 60, 32, 11, 40, 16, 4, 0, 10, 0, 5, 3, 1, 2, 0, 0, 2, 0, 1, 1, 0,
134, 30, 10, 10, 0, 11, 5, 3, 0, 4, 4, 0, 1, 1, 0, 0, 0, 1 ] ) ]
gap> piM:= piMbar[1]{ GetFusionMap( tbl2, facttbl ) };;
gap> s:= s0 * CharacterTable( "Cyclic", 2 );;
gap> piNbar:= PossiblePermutationCharacters( s, facttbl );
[ Character( CharacterTable( "HS.2" ),
[ 2200, 120, 0, 22, 0, 16, 8, 0, 20, 0, 0, 6, 2, 0, 0, 0, 0, 0, 0, 2, 0,
212, 20, 20, 12, 0, 2, 8, 2, 0, 0, 2, 0, 0, 2, 0, 0, 0, 2 ] ) ]
gap> piN:= piNbar[1]{ GetFusionMap( tbl2, facttbl ) };;
gap> piU:= PossiblePermutationCharacters( s0, tbl2 );
[ Character( CharacterTable( "2.HS.2" ),
[ 8800, 0, 320, 160, 0, 88, 0, 0, 32, 16, 0, 0, 80, 0, 0, 0, 0, 8, 16, 8,
0, 0, 0, 0, 0, 0, 0, 0, 0, 8, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ] ) ]
gap> ProofOfD8Factor( tbl2, piU[1], piM, piN );
[ [ 5, 17, 26 ], [ ] ]
The group (2.HS.2)∗ of the isoclinism type that is not printed
in the ATLAS has no faithful multiplicity-free permutation action.
gap> tbl2:= IsoclinicTable( tbl, tbl2, facttbl );;
gap> faith:= FaithfulCandidates( tbl2, "HS.2" );;
gap> CompareWithDatabase( "Isoclinic(2.HS.2)", faith );
3.15 G = 3.J3
The group 3.J3 has no faithful multiplicity-free permutation action.
gap> tbl:= CharacterTable( "3.J3" );;
gap> faith:= FaithfulCandidates( tbl, "J3" );;
gap> CompareWithDatabase( "3.J3", faith );
3.16 G = 3.J3.2
The group 3.J3.2 has no faithful multiplicity-free permutation action.
gap> tbl2:= CharacterTable( "3.J3.2" );;
gap> faith:= FaithfulCandidates( tbl2, "J3.2" );;
gap> CompareWithDatabase( "3.J3.2", faith );
3.17 G = 3.McL
The group 3.McL has one faithful multiplicity-free permutation action,
with point stabilizer of the type 2.A8, by Lemma 2.1.
gap> tbl:= CharacterTable( "3.McL" );;
gap> faith:= FaithfulCandidates( tbl, "McL" );;
6: subgroup $2.A_8$, degree 66825 (1 cand.)
gap> VerifyCandidates( CharacterTable( "2.A8" ), tbl, 0, faith[6], "all" );
G = 3.McL: point stabilizer 2.A8, ranks [ 14 ]
[ "1a+252a+1750a+2772ab+5103abc+5544a+6336ab+8064ab+9625a" ]
gap> CompareWithDatabase( "3.McL", faith );
gap> CompareWithCandidatesByMaxes( "3.McL", faith );
3.18 G = 3.McL.2
The group 3.McL.2 has one faithful multiplicity-free permutation action,
with point stabilizer of the type (2.A8.2)∗,
by Lemma 2.2.
gap> tbl2:= CharacterTable( "3.McL.2" );;
gap> faith:= FaithfulCandidates( tbl2, "McL.2" );;
9: subgroup $2.S_8$, degree 66825 (1 cand.)
gap> s:= CharacterTable( "Isoclinic(2.A8.2)" );;
gap> VerifyCandidates( s, tbl, tbl2, faith[9], "all" );
G = 3.McL.2: point stabilizer Isoclinic(2.A8.2), ranks [ 10 ]
[ "1a^++252a^++1750a^++2772ab+5103a^+bc+5544a^++6336ab+8064ab+9625a^+" ]
gap> CompareWithDatabase( "3.McL.2", faith );
3.19 G = 2.Ru
The group 2.Ru has one faithful multiplicity-free permutation action,
with point stabilizer of the type 2F4(2)′,
by Lemma 2.1.
gap> tbl:= CharacterTable( "2.Ru" );;
gap> faith:= FaithfulCandidates( tbl, "Ru" );;
2: subgroup ${^2F_4(2)^{\prime}} \leq {^2F_4(2)^{\prime}}.2$, degree 16240 (
1 cand.)
gap> VerifyCandidates( CharacterTable( "2F4(2)'" ), tbl, 0, faith[2], "all" );
G = 2.Ru: point stabilizer 2F4(2)', ranks [ 9 ]
[ "1a+28ab+406a+783a+3276a+3654a+4032ab" ]
gap> CompareWithDatabase( "2.Ru", faith );
3.20 G = 2.Suz
The group 2.Suz has one faithful multiplicity-free permutation action,
with point stabilizer of the type U5(2), by Lemma 2.1.
gap> tbl:= CharacterTable( "2.Suz" );;
gap> faith:= FaithfulCandidates( tbl, "Suz" );;
4: subgroup $U_5(2)$, degree 65520 (1 cand.)
gap> VerifyCandidates( CharacterTable( "U5(2)" ), tbl, 0, faith[4], "all" );
G = 2.Suz: point stabilizer U5(2), ranks [ 10 ]
[ "1a+143a+364abc+5940a+12012a+14300a+16016ab" ]
gap> CompareWithDatabase( "2.Suz", faith );
3.21 G = 2.Suz.2
The group 2.Suz.2 that is printed in the ATLAS has four faithful
multiplicity-free permutation actions,
with point stabilizers of the types U5(2).2 (twice)
and 35:(M11 ×2) (twice), respectively.
gap> tbl2:= CharacterTable( "2.Suz.2" );;
gap> faith:= FaithfulCandidates( tbl2, "Suz.2" );;
8: subgroup $U_5(2).2$, degree 65520 (1 cand.)
12: subgroup $3^5:(M_{11} \times 2)$, degree 465920 (1 cand.)
We verify the conditions of Lemma 2.3 (ii).
gap> s0:= CharacterTable( "U5(2)" );;
gap> s:= CharacterTable( "U5(2).2" );;
gap> facttbl:= CharacterTable( "Suz.2" );;
gap> CheckConditionsForLemma3( s0, s, facttbl, tbl2, "all" );
2.Suz.2: U5(2).2 lifts to a direct product,
proved by squares in [ 1, 8, 13, 19, 31, 44 ].
gap> VerifyCandidates( s, tbl, tbl2, faith[8], "all" );
G = 2.Suz.2: point stabilizer U5(2).2, ranks [ 8 ]
[ "1a^++143a^-+364a^+bc+5940a^++12012a^-+14300a^-+16016ab" ]
gap> s0:= CharacterTable( "SuzM5" );
CharacterTable( "3^5:M11" )
gap> s:= CharacterTable( "Suz.2M6" );
CharacterTable( "3^5:(M11x2)" )
gap> CheckConditionsForLemma3( s0, s, facttbl, tbl2, "all" );
2.Suz.2: 3^5:(M11x2) lifts to a direct product,
proved by squares in [ 1, 4, 8, 10, 19, 22, 26, 39 ].
gap> VerifyCandidates( s, tbl, tbl2, faith[12], "all" );
G = 2.Suz.2: point stabilizer 3^5:(M11x2), ranks [ 14 ]
[ "1a^++364a^{\\pm}bc+5940a^++12012a^-+14300a^-+15015ab+15795a^++16016ab+54054\
a^++100100a^-b^{\\pm}" ]
gap> faith[8]:= faith[8]{ [ 1, 1 ] };;
gap> faith[12]:= faith[12]{ [ 1, 1 ] };;
gap> CompareWithDatabase( "2.Suz.2", faith );
The group (2.Suz.2)∗ of the isoclinism type that is not printed
in the ATLAS has no faithful multiplicity-free permutation action.
gap> tbl2:= IsoclinicTable( tbl, tbl2, facttbl );;
gap> faith:= FaithfulCandidates( tbl2, "Suz.2" );;
gap> CompareWithDatabase( "Isoclinic(2.Suz.2)", faith );
3.22 G = 3.Suz
The group 3.Suz has four faithful multiplicity-free permutation actions,
with point stabilizers of the types G2(4), U5(2),
21+6−.U4(2), and 24+6:3A6, respectively,
by Lemma 2.1.
gap> tbl:= CharacterTable( "3.Suz" );;
gap> faith:= FaithfulCandidates( tbl, "Suz" );;
1: subgroup $G_2(4)$, degree 5346 (1 cand.)
4: subgroup $U_5(2)$, degree 98280 (1 cand.)
5: subgroup $2^{1+6}_-.U_4(2)$, degree 405405 (1 cand.)
6: subgroup $2^{4+6}:3A_6$, degree 1216215 (1 cand.)
gap> Maxes( tbl );
[ "3xG2(4)", "3^2.U4(3).2_3'", "3xU5(2)", "3x2^(1+6)_-.U4(2)", "3^6.M11",
"3xJ2.2", "3x2^(4+6).3A6", "(A4x3.L3(4)).2", "3x2^(2+8):(A5xS3)",
"3xM12.2", "3.3^(2+4):2(A4x2^2).2", "(3.A6xA5):2", "(3^(1+2):4xA6).2",
"3xL3(3).2", "3xL3(3).2", "3xL2(25)", "3.A7" ]
gap> VerifyCandidates( CharacterTable( "G2(4)" ), tbl, 0, faith[1], "all" );
G = 3.Suz: point stabilizer G2(4), ranks [ 7 ]
[ "1a+66ab+780a+1001a+1716ab" ]
gap> VerifyCandidates( CharacterTable( "U5(2)" ), tbl, 0, faith[4], "all" );
G = 3.Suz: point stabilizer U5(2), ranks [ 14 ]
[ "1a+78ab+143a+364a+1365ab+4290ab+5940a+12012a+14300a+27027ab" ]
gap> VerifyCandidates( CharacterTable( "SuzM4" ), tbl, 0, faith[5], "all" );
G = 3.Suz: point stabilizer 2^1+6.u4q2, ranks [ 23 ]
[ "1a+66ab+143a+429ab+780a+1716ab+3432a+5940a+6720ab+14300a+18954abc+25025a+42\
900ab+64350cd+66560a" ]
gap> VerifyCandidates( CharacterTable( "SuzM7" ), tbl, 0, faith[6], "all" );
G = 3.Suz: point stabilizer 2^4+6:3a6, ranks [ 27 ]
[ "1a+364a+780a+1001a+1365ab+4290ab+5940a+12012a+14300a+15795a+25025a+27027ab+\
42900ab+66560a+75075a+85800ab+88452a+100100a+104247ab+139776ab" ]
gap> CompareWithDatabase( "3.Suz", faith );
3.23 G = 3.Suz.2
The group 3.Suz.2 has four faithful multiplicity-free permutation actions,
with point stabilizers of the types G2(4).2, U5(2).2,
21+6−.U4(2).2, and 24+6:3S6, respectively.
We know from the treatment of 3.Suz that we can apply
Lemma 2.2.
gap> tbl2:= CharacterTable( "3.Suz.2" );;
gap> faith:= FaithfulCandidates( tbl2, "Suz.2" );;
1: subgroup $G_2(4).2$, degree 5346 (1 cand.)
8: subgroup $U_5(2).2$, degree 98280 (1 cand.)
10: subgroup $2^{1+6}_-.U_4(2).2$, degree 405405 (1 cand.)
13: subgroup $2^{4+6}:3S_6$, degree 1216215 (1 cand.)
gap> Maxes( CharacterTable( "Suz.2" ) );
[ "Suz", "G2(4).2", "3_2.U4(3).(2^2)_{133}", "U5(2).2", "2^(1+6)_-.U4(2).2",
"3^5:(M11x2)", "J2.2x2", "2^(4+6):3S6", "(A4xL3(4):2_3):2",
"2^(2+8):(S5xS3)", "M12.2x2", "3^(2+4):2(S4xD8)", "(A6:2_2xA5).2",
"(3^2:8xA6).2", "L2(25).2_2", "A7.2" ]
gap> VerifyCandidates( CharacterTable( "G2(4).2" ), tbl, tbl2, faith[1], "all" );
G = 3.Suz.2: point stabilizer G2(4).2, ranks [ 5 ]
[ "1a^++66ab+780a^++1001a^++1716ab" ]
gap> VerifyCandidates( CharacterTable( "U5(2).2" ), tbl, tbl2, faith[8], "all" );
G = 3.Suz.2: point stabilizer U5(2).2, ranks [ 10 ]
[ "1a^++78ab+143a^-+364a^++1365ab+4290ab+5940a^++12012a^-+14300a^-+27027ab" ]
gap> VerifyCandidates( CharacterTable( "Suz.2M5" ), tbl, tbl2, faith[10], "all" );
G = 3.Suz.2: point stabilizer 2^(1+6)_-.U4(2).2, ranks [ 16 ]
[ "1a^++66ab+143a^-+429ab+780a^++1716ab+3432a^++5940a^++6720ab+14300a^-+18954a\
^-bc+25025a^++42900ab+64350cd+66560a^+" ]
gap> VerifyCandidates( CharacterTable( "Suz.2M8" ), tbl, tbl2, faith[13], "all" );
G = 3.Suz.2: point stabilizer 2^(4+6):3S6, ranks [ 20 ]
[ "1a^++364a^++780a^++1001a^++1365ab+4290ab+5940a^++12012a^-+14300a^-+15795a^+\
+25025a^++27027ab+42900ab+66560a^++75075a^++85800ab+88452a^++100100a^++104247a\
b+139776ab" ]
gap> CompareWithDatabase( "3.Suz.2", faith );
3.24 G = 6.Suz
The group 6.Suz has one faithful multiplicity-free permutation action,
with point stabilizer of the type U5(2), by Lemma 2.1.
gap> tbl:= CharacterTable( "6.Suz" );;
gap> faith:= FaithfulCandidates( tbl, "2.Suz" );;
1: subgroup $U_5(2) \rightarrow (Suz,4)$, degree 196560 (1 cand.)
gap> VerifyCandidates( CharacterTable( "U5(2)" ), tbl, 0, faith[1], "all" );
G = 6.Suz: point stabilizer U5(2), ranks [ 26 ]
[ "1a+12ab+78ab+143a+364abc+924ab+1365ab+4290ab+4368ab+5940a+12012a+14300a+160\
16ab+27027ab+27456ab" ]
gap> CompareWithDatabase( "6.Suz", faith );
3.25 G = 6.Suz.2
The group 6.Suz.2 that is printed in the ATLAS has two faithful
multiplicity-free permutation actions,
with point stabilizers of the type U5(2).2 (twice).
We know from the treatment of 6.Suz that we can apply
Lemma 2.2,
and get two classes in each case by the treatment of 2.Suz.2.
gap> tbl2:= CharacterTable( "6.Suz.2" );;
gap> faith:= FaithfulCandidates( tbl2, "Suz.2" );;
8: subgroup $U_5(2).2$, degree 196560 (1 cand.)
gap> VerifyCandidates( CharacterTable( "U5(2).2" ), tbl, tbl2, faith[8], "all" );
G = 6.Suz.2: point stabilizer U5(2).2, ranks [ 16 ]
[ "1a^++12ab+78ab+143a^-+364a^+bc+924ab+1365ab+4290ab+4368ab+5940a^++12012a^-+\
14300a^-+16016ab+27027ab+27456ab" ]
gap> faith[8]:= faith[8]{ [ 1, 1 ] };;
gap> CompareWithDatabase( "6.Suz.2", faith );
It follows from the treatment of (2.Suz.2)∗
that the group (6.Suz.2)∗
of the isoclinism type that is not printed in the ATLAS does not have a
faithful multiplicity-free permutation action.
gap> CompareWithDatabase( "Isoclinic(6.Suz.2)", [] );
3.26 G = 3.ON
The group 3.ON has four faithful multiplicity-free permutation actions,
with point stabilizers of the types L3(7).2 (twice) and L3(7) (twice).
(The Schur multiplier of L3(7).2 is trivial, so the L3(7) type
subgroups lift to direct products with the centre of 3.ON, that is,
we can apply Lemma 2.1.)
gap> tbl:= CharacterTable( "3.ON" );;
gap> faith:= FaithfulCandidates( tbl, "ON" );;
1: subgroup $L_3(7).2$, degree 368280 (1 cand.)
2: subgroup $L_3(7) \leq L_3(7).2$, degree 736560 (1 cand.)
3: subgroup $L_3(7).2$, degree 368280 (1 cand.)
4: subgroup $L_3(7) \leq L_3(7).2$, degree 736560 (1 cand.)
gap> VerifyCandidates( CharacterTable( "L3(7).2" ), tbl, 0,
> Concatenation( faith[1], faith[3] ), "all" );
G = 3.ON: point stabilizer L3(7).2, ranks [ 11, 11 ]
[ "1a+495ab+10944a+26752a+32395b+52668a+58653bc+63612ab",
"1a+495cd+10944a+26752a+32395a+52668a+58653bc+63612ab" ]
gap> VerifyCandidates( CharacterTable( "L3(7)" ), tbl, 0,
> Concatenation( faith[2], faith[4] ), "all" );
G = 3.ON: point stabilizer L3(7), ranks [ 15, 15 ]
[ "1a+495ab+10944a+26752a+32395b+37696a+52668a+58653bc+63612ab+85064a+122760ab\
",
"1a+495cd+10944a+26752a+32395a+37696a+52668a+58653bc+63612ab+85064a+122760ab\
" ]
gap> CompareWithDatabase( "3.ON", faith );
3.27 G = 3.ON.2
The group 3.ON.2 has no faithful multiplicity-free permutation action.
gap> tbl2:= CharacterTable( "3.ON.2" );;
gap> faith:= FaithfulCandidates( tbl2, "ON.2" );;
gap> CompareWithDatabase( "3.ON.2", faith );
3.28 G = 2.Fi22
The group 2.Fi22 has seven faithful multiplicity-free permutation
actions, with point stabilizers of the types O7(3) (twice), O8+(2):S3
(twice), O8+(2):3, and O8+(2):2 (twice).
gap> tbl:= CharacterTable( "2.Fi22" );;
gap> faith:= FaithfulCandidates( tbl, "Fi22" );;
2: subgroup $O_7(3)$, degree 28160 (2 cand.)
3: subgroup $O_7(3)$, degree 28160 (2 cand.)
4: subgroup $O_8^+(2):S_3$, degree 123552 (2 cand.)
5: subgroup $O_8^+(2):3 \leq O_8^+(2):S_3$, degree 247104 (1 cand.)
6: subgroup $O_8^+(2):2 \leq O_8^+(2):S_3$, degree 370656 (2 cand.)
The two classes of maximal subgroups of the type O7(3) in Fi22 induce
the same permutation character and lift to two classes of the type
2 ×O7(3) in 2.Fi22.
We get the same two candidates for these two classes.
One of them belongs to the first class of O7(3) subgroups in 2.Fi22,
the other candidate belongs to the second class;
this can be seen from the fact that the outer automorphism of Fi22
swaps the two classes of O7(3) subgroups, and the lift of this automorphism
to 2.Fi22 interchanges the candidates
-this action can be read off from the embedding of 2.Fi22 into any group
of the type 2.Fi22.2.
gap> faith[2] = faith[3];
true
gap> tbl2:= CharacterTable( "2.Fi22.2" );;
gap> embed:= GetFusionMap( tbl, tbl2 );;
gap> swapped:= Filtered( InverseMap( embed ), IsList );
[ [ 3, 4 ], [ 17, 18 ], [ 25, 26 ], [ 27, 28 ], [ 33, 34 ], [ 36, 37 ],
[ 42, 43 ], [ 51, 52 ], [ 59, 60 ], [ 63, 65 ], [ 64, 66 ], [ 71, 72 ],
[ 73, 75 ], [ 74, 76 ], [ 81, 82 ], [ 85, 87 ], [ 86, 88 ], [ 89, 90 ],
[ 93, 94 ], [ 95, 98 ], [ 96, 97 ], [ 99, 100 ], [ 103, 104 ],
[ 107, 110 ], [ 108, 109 ], [ 113, 114 ] ]
gap> perm:= Product( List( swapped, pair -> ( pair[1], pair[2] ) ) );;
gap> Permuted( faith[2][1], perm ) = faith[2][2];
true
gap> VerifyCandidates( CharacterTable( "O7(3)" ), tbl, 0, faith[2], "all" );
G = 2.Fi22: point stabilizer O7(3), ranks [ 5, 5 ]
[ "1a+352a+429a+13650a+13728b", "1a+352a+429a+13650a+13728a" ]
gap> faith[2]:= [ faith[2][1] ];;
gap> faith[3]:= [ faith[3][2] ];;
All involutions in Fi22 lift to involutions in 2.Fi22,
so the preimages of the maximal subgroups of the type O8+(2).S3
in Fi22 have the type 2 ×O8+(2).S3.
We apply Lemma 2.3, using that the two subgroups of the type
O8+(2).S3 contain involutions outside O8+(2) which lie in the two
nonconjugate preimages of the class 2A of Fi22;
this proves the existence of the two candidates of degree 123 552.
gap> s:= CharacterTable( "O8+(2).S3" );;
gap> s0:= CharacterTable( "O8+(2).3" );;
gap> facttbl:= CharacterTable( "Fi22" );;
gap> CheckConditionsForLemma3( s0, s, facttbl, tbl, "all" );
2.Fi22: O8+(2).3.2 lifts to a direct product,
proved by squares in [ 1, 8, 10, 12, 20, 23, 30, 46, 55, 61, 91 ].
gap> derpos:= ClassPositionsOfDerivedSubgroup( s );;
gap> factfus:= GetFusionMap( tbl, facttbl );;
gap> ForAll( PossibleClassFusions( s, tbl ),
> map -> NecessarilyDifferentPermChars( map, factfus, derpos ) );
true
gap> VerifyCandidates( CharacterTable( "O8+(2).S3" ), tbl, 0, faith[4], "all" );
G = 2.Fi22: point stabilizer O8+(2).3.2, ranks [ 6, 6 ]
[ "1a+3080a+13650a+13728b+45045a+48048c",
"1a+3080a+13650a+13728a+45045a+48048b" ]
The existence of one class of O8+(2).3 subgroups follows from
Lemma 2.1, and the proof for O8+(2).S3 also establishes
two classes of O8+(2).2 subgroups, with different permutation characters,
gap> VerifyCandidates( CharacterTable( "O8+(2).3" ), tbl, 0, faith[5], "all" );
G = 2.Fi22: point stabilizer O8+(2).3, ranks [ 11 ]
[ "1a+1001a+3080a+10725a+13650a+13728ab+45045a+48048bc+50050a" ]
gap> VerifyCandidates( CharacterTable( "O8+(2).2" ), tbl, 0, faith[6], "all" );
G = 2.Fi22: point stabilizer O8+(2).2, ranks [ 11, 11 ]
[ "1a+352a+429a+3080a+13650a+13728b+45045a+48048ac+75075a+123200a",
"1a+352a+429a+3080a+13650a+13728a+45045a+48048ab+75075a+123200a" ]
gap> CompareWithDatabase( "2.Fi22", faith );
3.29 G = 2.Fi22.2
The group 2.Fi22.2 that is printed in the ATLAS has six faithful
multiplicity-free permutation actions,
with point stabilizers of the types O7(3), O8+(2):S3,
O8+(2):3 ×2, O8+(2):2, and 2F4(2) (twice).
gap> tbl2:= CharacterTable( "2.Fi22.2" );;
gap> faith:= FaithfulCandidates( tbl2, "Fi22.2" );;
3: subgroup $O_7(3)$, degree 56320 (1 cand.)
5: subgroup $O_8^+(2):S_3 \leq O_8^+(2):S_3 \times 2$, degree 247104 (
1 cand.)
6: subgroup $O_8^+(2):3 \times 2 \leq O_8^+(2):S_3 \times 2$, degree 247104 (
1 cand.)
10: subgroup $O_8^+(2):2 \leq O_8^+(2):S_3 \times 2$, degree 741312 (1 cand.)
16: subgroup ${^2F_4(2)^{\prime}}.2$, degree 7185024 (1 cand.)
The third, fifth, and tenth multiplicity-free permutation character of
Fi22.2 are induced from subgroups of the types O7(3), O8+(2).S3,
and O8+(2).2 that lie inside Fi22, and we have discussed above that
these groups lift to direct products in 2.Fi22.
In fact all such subgroups of 2.Fi22.2 lie inside 2.Fi22,
and the two classes of such subgroups in 2.Fi22 are fused in
2.Fi22.2, hence we get only one class of these subgroups.
gap> VerifyCandidates( CharacterTable( "O7(3)" ), tbl, tbl2, faith[3], "all" );
G = 2.Fi22.2: point stabilizer O7(3), ranks [ 9 ]
[ "1a^{\\pm}+352a^{\\pm}+429a^{\\pm}+13650a^{\\pm}+13728ab" ]
gap> VerifyCandidates( CharacterTable( "O8+(2).S3" ), tbl, tbl2, faith[5], "all" );
G = 2.Fi22.2: point stabilizer O8+(2).3.2, ranks [ 10 ]
[ "1a^{\\pm}+3080a^{\\pm}+13650a^{\\pm}+13728ab+45045a^{\\pm}+48048bc" ]
gap> VerifyCandidates( CharacterTable( "O8+(2).2" ), tbl, tbl2, faith[10], "all" );
G = 2.Fi22.2: point stabilizer O8+(2).2, ranks [ 20 ]
[ "1a^{\\pm}+352a^{\\pm}+429a^{\\pm}+3080a^{\\pm}+13650a^{\\pm}+13728ab+45045a\
^{\\pm}+48048a^{\\pm}bc+75075a^{\\pm}+123200a^{\\pm}" ]
The sixth multiplicity-free permutation character of Fi22.2
is induced from a subgroup of the type O8+(2).3 ×2
that does not lie in Fi22.
Let M be a maximal subgroup of G = 2.Fi22.2 that maps onto a group
of the type O8+(2):S3 ×2 in the factor group Fi22.2.
As we have discussed above, any O8+(2).3 type subgroup of Fi22
lifts to a subgroup of the type 2 ×O8+(2).3 in 2.Fi22,
and the outer involutions in the subgroup O8+(2).3 ×2 of Fi22.2
lift to involutions in 2.Fi22.2; so M contains two subgroups
isomorphic to H that do not contain the centre of 2.Fi22.2.
We use Lemma 2.4 to show that these groups are conjugate in M:
The subgroup U has the type O8+(2).3,
the subgroups H and U Z have the type O8+(2):3 ×2,
and so also N/Z has this type.
gap> tbl2:= CharacterTable( "2.Fi22.2" );;
gap> facttbl:= CharacterTable( "Fi22.2" );;
gap> tblMbar:= CharacterTable( "O8+(2).S3" ) * CharacterTable( "Cyclic", 2 );;
gap> piMbar:= PossiblePermutationCharacters( tblMbar, facttbl );
[ Character( CharacterTable( "Fi22.2" ),
[ 61776, 6336, 656, 288, 666, 216, 36, 27, 40, 76, 16, 12, 20, 1, 36, 72,
8, 26, 18, 36, 24, 12, 8, 6, 3, 1, 4, 8, 0, 2, 6, 3, 0, 1, 1, 0, 4, 10,
4, 4, 0, 0, 4, 2, 4, 3, 0, 1, 1, 0, 0, 3, 2, 1, 1, 0, 2, 4, 1, 1576,
216, 316, 168, 56, 36, 32, 4, 46, 64, 10, 16, 10, 30, 10, 1, 9, 6, 4,
4, 8, 0, 6, 1, 1, 1, 24, 6, 6, 6, 8, 6, 6, 0, 2, 1, 1, 1, 0, 4, 1, 1,
0, 1, 4, 2, 0, 0, 0, 1, 1, 0, 1 ] ) ]
gap> piM:= piMbar[1]{ GetFusionMap( tbl2, facttbl ) };;
gap> tblNbar:= CharacterTable( "O8+(2).3" ) * CharacterTable( "Cyclic", 2 );;
gap> piNbar:= PossiblePermutationCharacters( tblNbar, facttbl );
[ Character( CharacterTable( "Fi22.2" ),
[ 123552, 0, 1312, 192, 1332, 432, 72, 54, 80, 0, 0, 24, 16, 2, 0, 0, 16,
52, 0, 48, 0, 24, 16, 0, 6, 2, 4, 4, 0, 0, 12, 6, 0, 0, 2, 0, 8, 20, 8,
0, 0, 0, 0, 4, 0, 6, 0, 0, 2, 0, 0, 0, 4, 0, 2, 0, 4, 4, 0, 3152, 432,
0, 48, 80, 48, 0, 8, 92, 128, 20, 0, 20, 60, 0, 2, 18, 12, 0, 4, 4, 0,
0, 2, 0, 2, 24, 12, 12, 0, 8, 12, 0, 0, 0, 2, 2, 0, 0, 8, 2, 0, 0, 0,
4, 4, 0, 0, 0, 2, 0, 0, 2 ] ) ]
gap> piN:= piNbar[1]{ GetFusionMap( tbl2, facttbl ) };;
gap> tblU:= CharacterTable( "O8+(2).3" );;
gap> piU:= PossiblePermutationCharacters( tblU, tbl2 );
[ Character( CharacterTable( "2.Fi22.2" ),
[ 494208, 0, 0, 4608, 640, 384, 5328, 0, 1728, 0, 288, 0, 216, 0, 160, 0,
0, 96, 0, 32, 8, 0, 0, 0, 0, 64, 96, 112, 0, 96, 0, 0, 96, 48, 16, 0,
0, 24, 8, 0, 8, 8, 0, 0, 48, 0, 24, 0, 0, 0, 0, 8, 0, 0, 0, 16, 64, 16,
16, 0, 0, 0, 0, 0, 0, 8, 0, 24, 0, 0, 0, 0, 8, 0, 0, 0, 0, 0, 0, 16, 0,
8, 0, 0, 0, 8, 8, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ] ) ]
gap> ProofOfD8Factor( tbl2, piU[1], piM, piN );
[ [ 91, 101, 104, 110, 114, 116, 124, 130, 135, 138, 146 ], [ 3 ] ]
Since also 2.Fi22 contains subgroups of the type O8+(2).3 ×2,
we must use "extending" as the last argument of VerifyCandidates.
gap> s:= CharacterTable( "O8+(2).3" ) * CharacterTable( "Cyclic", 2 );;
gap> VerifyCandidates( s, tbl, tbl2, faith[6], "extending" );
G = 2.Fi22.2: point stabilizer O8+(2).3xC2, ranks [ 9 ]
[ "1a^++1001a^-+3080a^++10725a^++13650a^++13728ab+45045a^++48048bc+50050a^+" ]
By Lemma 2.3, the subgroup 2F4(2) of Fi22.2 lifts
to 2 ×2F4(2) in 2.Fi22.2;
for that, note that the class 4D of 2F4(2) does not lie inside
2F4(2)′ and the preimages in 2.Fi22.2 of the images in
Fi22.2 square into the subgroup 2F4(2)′ of the direct
product 2 ×2F4(2)′.
Since the group 2 ×2F4(2) contains two subgroups of the type
2F4(2), with normalizer 2 ×2F4(2), there are two classes
of such subgroups, which induce the same permutation character.
gap> facttbl:= CharacterTable( "Fi22.2" );;
gap> s0:= CharacterTable( "2F4(2)'" );;
gap> s:= CharacterTable( "2F4(2)" );;
gap> CheckConditionsForLemma3( s0, s, facttbl, tbl2, "all" );
2.Fi22.2: 2F4(2)'.2 lifts to a direct product,
proved by squares in [ 5, 38, 53 ].
gap> VerifyCandidates( s, tbl, tbl2, faith[16], "all" );
G = 2.Fi22.2: point stabilizer 2F4(2)'.2, ranks [ 13 ]
[ "1a^++1001a^++1430a^++13650a^++30030a^++133056a^{\\pm}+289575a^-+400400ab+57\
9150a^++675675a^-+1201200a^-+1663200ab" ]
gap> faith[16]:= faith[16]{ [ 1, 1 ] };;
gap> CompareWithDatabase( "2.Fi22.2", faith );
The group (2.Fi22.2)∗ of the isoclinism type that is not printed
in the ATLAS has five faithful multiplicity-free permutation actions,
with point stabilizers of the types O7(3), O8+(2):S3 (twice),
and O8+(2):2 (twice).
gap> tbl2:= IsoclinicTable( tbl, tbl2, facttbl );;
gap> faith:= FaithfulCandidates( tbl2, "Fi22.2" );;
3: subgroup $O_7(3)$, degree 56320 (1 cand.)
5: subgroup $O_8^+(2):S_3 \leq O_8^+(2):S_3 \times 2$, degree 247104 (
1 cand.)
7: subgroup $O_8^+(2):S_3 \leq O_8^+(2):S_3 \times 2$, degree 247104 (
1 cand.)
10: subgroup $O_8^+(2):2 \leq O_8^+(2):S_3 \times 2$, degree 741312 (1 cand.)
11: subgroup $O_8^+(2):2 \leq O_8^+(2):S_3 \times 2$, degree 741312 (1 cand.)
The characters arising from the third, fifth, and tenth multiplicity-free
permutation character of Fi22.2 are induced from subgroups of
2.Fi22, so these actions have been verified above.
The seventh multiplicity-free permutation character of Fi22.2
is induced from a subgroup of the type O8+(2).S3
that does not lie in Fi22.
By Lemma 2.3 (i), this subgroup lifts to a direct
product N in G = (2.Fi22.2)∗.
gap> tblU:= CharacterTable( "O8+(2).3" );;
gap> tblNbar:= CharacterTable( "O8+(2).S3" );;
gap> CheckConditionsForLemma3( tblU, tblNbar, facttbl, tbl2, "extending" );
Isoclinic(2.Fi22.2): O8+(2).3.2 lifts to a direct product,
proved by squares in [ 1, 7, 9, 11, 18, 21, 26, 39, 47, 52, 73 ].
The G-conjugacy of the two subgroups of the type O8+(2).S3 in N
follows from Lemma 2.4.
Note that there are two permutation characters of G that are induced from
O8+(2).S3 type subgroups,
and the permutation character 1NG is determined as the one that does
not vanish outside G′.
gap> tblNbar:= CharacterTable( "O8+(2).S3" );;
gap> piNbar:= PossiblePermutationCharacters( tblNbar, facttbl );
[ Character( CharacterTable( "Fi22.2" ),
[ 123552, 0, 1312, 192, 1332, 432, 72, 54, 80, 0, 0, 24, 16, 2, 0, 0, 16,
52, 0, 48, 0, 24, 16, 0, 6, 2, 4, 4, 0, 0, 12, 6, 0, 0, 2, 0, 8, 20, 8,
0, 0, 0, 0, 4, 0, 6, 0, 0, 2, 0, 0, 0, 4, 0, 2, 0, 4, 4, 0, 0, 0, 632,
288, 32, 24, 64, 0, 0, 0, 0, 32, 0, 0, 20, 0, 0, 0, 8, 4, 12, 0, 12, 0,
2, 0, 24, 0, 0, 12, 8, 0, 12, 0, 4, 0, 0, 2, 0, 0, 0, 2, 0, 2, 4, 0, 0,
0, 0, 0, 2, 0, 0 ] ), Character( CharacterTable( "Fi22.2" ),
[ 123552, 12672, 1312, 576, 1332, 432, 72, 54, 80, 152, 32, 24, 40, 2, 72,
144, 16, 52, 36, 72, 48, 24, 16, 12, 6, 2, 8, 16, 0, 4, 12, 6, 0, 2, 2,
0, 8, 20, 8, 8, 0, 0, 8, 4, 8, 6, 0, 2, 2, 0, 0, 6, 4, 2, 2, 0, 4, 8,
2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0 ] ) ]
gap> piN:= piNbar[1]{ GetFusionMap( tbl2, facttbl ) };;
gap> ProofOfD8Factor( tbl2, piU[1], piM, piN );
[ [ 89, 90, 97, 98, 99, 100, 102, 103, 105, 106, 107, 108, 109, 115, 117,
119, 127, 128, 129, 132, 133, 134, 145, 149, 150 ], [ 3 ] ]
Since also 2.Fi22 contains subgroups of the type O8+(2):S3,
we must use "extending" as the last argument of VerifyCandidates.
gap> s0:= CharacterTable( "O8+(2).3" );;
gap> s:= CharacterTable( "O8+(2).S3" );;
gap> CheckConditionsForLemma3( s0, s, facttbl, tbl2, "extending" );
Isoclinic(2.Fi22.2): O8+(2).3.2 lifts to a direct product,
proved by squares in [ 1, 7, 9, 11, 18, 21, 26, 39, 47, 52, 73 ].
gap> VerifyCandidates( s, tbl, tbl2, faith[7], "extending" );
G = Isoclinic(2.Fi22.2): point stabilizer O8+(2).3.2, ranks [ 9 ]
[ "1a^++1001a^++3080a^++10725a^-+13650a^++13728ab+45045a^++48048bc+50050a^-" ]
The existence of exactly one class of O8+(2):2 type subgroups
not contained in 2.Fi22 follows from the above consideration;
the corresponding permutation characters arise from the 11-th
multiplicity-free permutation character of Fi22.2.
gap> s:= CharacterTable( "O8+(2).2" );;
gap> VerifyCandidates( s, tbl, tbl2, faith[11], "extending" );
G = Isoclinic(2.Fi22.2): point stabilizer O8+(2).2, ranks [ 19 ]
[ "1a^++352a^{\\pm}+429a^{\\pm}+1001a^++3080a^++10725a^-+13650a^++13728ab+4504\
5a^++48048a^{\\pm}bc+50050a^-+75075a^{\\pm}+123200a^{\\pm}" ]
gap> CompareWithDatabase( "Isoclinic(2.Fi22.2)", faith );
3.30 G = 3.Fi22
The group 3.Fi22 has six faithful multiplicity-free permutation actions,
with point stabilizers of the types O8+(2):S3, O8+(2):3 (twice),
O8+(2):2, 26:S6(2), and 2F4(2)′.
gap> tbl:= CharacterTable( "3.Fi22" );;
gap> faith:= FaithfulCandidates( tbl, "Fi22" );;
4: subgroup $O_8^+(2):S_3$, degree 185328 (1 cand.)
5: subgroup $O_8^+(2):3 \leq O_8^+(2):S_3$, degree 370656 (2 cand.)
6: subgroup $O_8^+(2):2 \leq O_8^+(2):S_3$, degree 555984 (1 cand.)
8: subgroup $2^6:S_6(2)$, degree 2084940 (1 cand.)
9: subgroup ${^2F_4(2)^{\prime}}$, degree 10777536 (1 cand.)
The preimages of the maximal subgroups of the type O8+(2).S3 in Fi22
have the type 3 ×O8+(2).S3,
because the Schur multiplier of O8+(2) has order 4 and the only central
extension of S3 by a group of order 3 is 3 ×S3.
Each such preimage contains one subgroup of the type O8+(2).S3
with one subgroup of the type O8+(2).3,
two conjugate O8+(2).3 subgroups which are not contained in O8+(2).S3,
and one class of O8+(2).2 subgroups.
The two classes of O8+(2).3 subgroups contain elements of order 3
outside O8+(2) which lie in nonconjugate preimages of the class 3A
of Fi22, so we get two classes of O8+(2).3 subgroups in 3.Fi22
which induce different permutation characters.
gap> VerifyCandidates( CharacterTable( "O8+(2).S3" ), tbl, 0, faith[4], "all" );
G = 3.Fi22: point stabilizer O8+(2).3.2, ranks [ 10 ]
[ "1a+351ab+3080a+13650a+19305ab+42120ab+45045a" ]
gap> s:= CharacterTable( "O8+(2).3" );;
gap> fus:= PossibleClassFusions( s, tbl );;
gap> facttbl:= CharacterTable( "Fi22" );;
gap> factfus:= GetFusionMap( tbl, facttbl );;
gap> outer:= Difference( [ 1 .. NrConjugacyClasses( s ) ],
> ClassPositionsOfDerivedSubgroup( s ) );;
gap> outerfus:= List( fus, map -> map{ outer } );
[ [ 13, 13, 18, 18, 46, 46, 50, 50, 59, 59, 75, 75, 95, 95, 98, 98, 95, 95,
116, 116, 142, 142, 148, 148, 157, 157, 160, 160 ],
[ 14, 15, 18, 18, 47, 48, 51, 52, 59, 59, 76, 77, 96, 97, 99, 100, 96, 97,
116, 116, 143, 144, 149, 150, 158, 159, 161, 162 ],
[ 15, 14, 18, 18, 48, 47, 52, 51, 59, 59, 77, 76, 97, 96, 100, 99, 97, 96,
116, 116, 144, 143, 150, 149, 159, 158, 162, 161 ] ]
gap> preim:= InverseMap( factfus )[5];
[ 13, 14, 15 ]
gap> List( outerfus, x -> List( preim, i -> i in x ) );
[ [ true, false, false ], [ false, true, true ], [ false, true, true ] ]
gap> VerifyCandidates( s, tbl, 0, faith[5], "all" );
G = 3.Fi22: point stabilizer O8+(2).3, ranks [ 11, 17 ]
[ "1a+1001a+3080a+10725a+13650a+27027ab+45045a+50050a+96525ab",
"1a+351ab+1001a+3080a+7722ab+10725a+13650a+19305ab+42120ab+45045a+50050a+540\
54ab" ]
gap> VerifyCandidates( CharacterTable( "O8+(2).2" ), tbl, 0, faith[6], "all" );
G = 3.Fi22: point stabilizer O8+(2).2, ranks [ 17 ]
[ "1a+351ab+429a+3080a+13650a+19305ab+27027ab+42120ab+45045a+48048a+75075a+965\
25ab" ]
Lemma 2.1 applies to the maximal subgroups of the types
26:S6(2) and 2F4(2)′ in Fi22 and their preimages
in 3.Fi22.
gap> VerifyCandidates( CharacterTable( "2^6:s6f2" ), tbl, 0, faith[8], "all" );
G = 3.Fi22: point stabilizer 2^6:s6f2, ranks [ 24 ]
[ "1a+351ab+429a+1430a+3080a+13650a+19305ab+27027ab+30030a+42120ab+45045a+7507\
5a+96525ab+123552ab+205920a+320320a+386100ab" ]
gap> VerifyCandidates( CharacterTable( "2F4(2)'" ), tbl, 0, faith[9], "all" );
G = 3.Fi22: point stabilizer 2F4(2)', ranks [ 25 ]
[ "1a+1001a+1430a+13650a+19305ab+27027ab+30030a+51975ab+289575a+386100ab+40040\
0ab+405405ab+579150a+675675a+1201200a+1351350efgh" ]
gap> CompareWithDatabase( "3.Fi22", faith );
3.31 G = 3.Fi22.2
The group 3.Fi22.2 has seven faithful multiplicity-free permutation
actions,
with point stabilizers of the types O8+(2):S3 ×2,
O8+(2):3 ×2, O8+(2):S3 (twice), O8+(2):2 ×2,
27:S6(2), and 2F4(2).
gap> tbl2:= CharacterTable( "3.Fi22.2" );;
gap> faith:= FaithfulCandidates( tbl2, "Fi22.2" );;
4: subgroup $O_8^+(2):S_3 \times 2$, degree 185328 (1 cand.)
6: subgroup $O_8^+(2):3 \times 2 \leq O_8^+(2):S_3 \times 2$, degree 370656 (
1 cand.)
7: subgroup $O_8^+(2):S_3 \leq O_8^+(2):S_3 \times 2$, degree 370656 (
2 cand.)
8: subgroup $O_8^+(2):2 \times 2 \leq O_8^+(2):S_3 \times 2$, degree 555984 (
1 cand.)
9: subgroup $O_8^+(2):3 \leq O_8^+(2):S_3 \times 2$, degree 741312 (1 cand.)
14: subgroup $2^7:S_6(2)$, degree 2084940 (1 cand.)
16: subgroup ${^2F_4(2)^{\prime}}.2$, degree 10777536 (1 cand.)
Let H be a subgroup of the type O8+(2):S3 ×2 in Fi22.2;
it induces the 4-th multiplicity-free permutation character of Fi22.2.
The intersection of H with Fi22 is of the type O8+(2):S3;
it lifts to a direct product in 3.Fi22, which contains one subgroup
of the type O8+(2):S3 that is normal in the preimage of H.
By Lemma 2.2, we get one class of subgroups of the type
O8+(2):S3 ×2 in 3.Fi22.2.
The same argument yields one class of each of the types O8+(2):3 ×2
and O8+(2):2 ×2,
which arise from the 6-th and 8-th multiplicity-free permutation character
of Fi22.2, respectively.
gap> s:= CharacterTable( "O8+(2).S3" ) * CharacterTable( "Cyclic", 2 );;
gap> VerifyCandidates( s, tbl, tbl2, faith[4], "all" );
G = 3.Fi22.2: point stabilizer O8+(2).3.2xC2, ranks [ 7 ]
[ "1a^++351ab+3080a^++13650a^++19305ab+42120ab+45045a^+" ]
gap> s:= CharacterTable( "O8+(2).3" ) * CharacterTable( "Cyclic", 2 );;
gap> VerifyCandidates( s, tbl, tbl2, faith[6], "all" );
G = 3.Fi22.2: point stabilizer O8+(2).3xC2, ranks [ 12 ]
[ "1a^++351ab+1001a^-+3080a^++7722ab+10725a^++13650a^++19305ab+42120ab+45045a^\
++50050a^++54054ab" ]
gap> s:= CharacterTable( "O8+(2).2" ) * CharacterTable( "Cyclic", 2 );;
gap> VerifyCandidates( s, tbl, tbl2, faith[8], "all" );
G = 3.Fi22.2: point stabilizer O8+(2).2xC2, ranks [ 12 ]
[ "1a^++351ab+429a^++3080a^++13650a^++19305ab+27027ab+42120ab+45045a^++48048a^\
++75075a^++96525ab" ]
Let H be a subgroup of the type O8+(2):S3 in Fi22.2 that is not
contained in Fi22; it induces the 7-th multiplicity-free
permutation character of Fi22.2.
The intersection of H with Fi22 is of the type O8+(2):3;
it lifts to a direct product in 3.Fi22, which contains four subgroups
of the type O8+(2):3,
three of them not containing the centre of 3.Fi22.
By Lemma 2.2, we get three subgroups of the type
O8+(2):S3 in 3.Fi22.2, two of which are conjugate;
they induce two different permutation characters, so we get two classes.
(Since there are O8+(2).S3 type subgroups also inside 3.Fi22,
we must use "extending" as the last argument of VerifyCandidates.)
gap> s:= CharacterTable( "O8+(2).S3" );;
gap> derpos:= ClassPositionsOfDerivedSubgroup( s );;
gap> facttbl:= CharacterTable( "Fi22.2" );;
gap> sfustbl2:= PossibleClassFusions( s, tbl2,
> rec( permchar:= faith[7][1] ) );;
gap> ForAll( sfustbl2,
> map -> NecessarilyDifferentPermChars( map, factfus, derpos ) );
true
gap> VerifyCandidates( s, tbl, tbl2, faith[7], "extending" );
G = 3.Fi22.2: point stabilizer O8+(2).3.2, ranks [ 9, 12 ]
[ "1a^++1001a^++3080a^++10725a^-+13650a^++27027ab+45045a^++50050a^-+96525ab",
"1a^++351ab+1001a^++3080a^++7722ab+10725a^-+13650a^++19305ab+42120ab+45045a^\
++50050a^-+54054ab" ]
The nineth multiplicity-free permutation character of Fi22.2
is induced from a subgroup of the type O8+(2).3 that lies inside Fi22
and is known to lift to s group of the type 3 ×O8+(2).3
in 3.Fi22.
All subgroups of index three in this group either contain the centre of
3.Fi22 or have the type O8+(2).3, and it turns out that the
permutation characters of 3.Fi22.2 induced from these subgroups are
not multiplicity-free.
So the candidate must be excluded.
gap> VerifyCandidates( CharacterTable( "O8+(2).3" ), tbl, tbl2, faith[9], "all" );
G = 3.Fi22.2: no O8+(2).3
gap> faith[9]:= [];;
Lemma 2.2 guarantees the existence of one class of subgroups
of each of the types 27:S6(2) and 2F4(2).
gap> VerifyCandidates( CharacterTable( "2^7:S6(2)" ), tbl, tbl2, faith[14], "all" );
G = 3.Fi22.2: point stabilizer 2^7:S6(2), ranks [ 17 ]
[ "1a^++351ab+429a^++1430a^++3080a^++13650a^++19305ab+27027ab+30030a^++42120ab\
+45045a^++75075a^++96525ab+123552ab+205920a^++320320a^++386100ab" ]
gap> VerifyCandidates( CharacterTable( "2F4(2)" ), tbl, tbl2, faith[16], "all" );
G = 3.Fi22.2: point stabilizer 2F4(2)'.2, ranks [ 17 ]
[ "1a^++1001a^++1430a^++13650a^++19305ab+27027ab+30030a^++51975ab+289575a^-+38\
6100ab+400400ab+405405ab+579150a^++675675a^-+1201200a^-+1351350efgh" ]
gap> CompareWithDatabase( "3.Fi22.2", faith );
3.32 G = 6.Fi22
The group 6.Fi22 has six faithful multiplicity-free permutation actions,
with point stabilizers of the types O8+(2):S3 (twice),
O8+(2):3 (twice), and O8+(2):2 (twice).
gap> tbl:= CharacterTable( "6.Fi22" );;
gap> facttbl:= CharacterTable( "3.Fi22" );;
gap> faith:= FaithfulCandidates( tbl, "3.Fi22" );;
1: subgroup $O_8^+(2):S_3 \rightarrow (Fi_{22},4)$, degree 370656 (2 cand.)
2: subgroup $O_8^+(2):3 \rightarrow (Fi_{22},5)$, degree 741312 (1 cand.)
3: subgroup $O_8^+(2):3 \rightarrow (Fi_{22},5)$, degree 741312 (1 cand.)
4: subgroup $O_8^+(2):2 \rightarrow (Fi_{22},6)$, degree 1111968 (2 cand.)
From the discussion of the cases 2.Fi22 and 3.Fi22,
we conclude that the maximal subgroups of the type O8+(2).S3 lift to
groups of the type 6 ×O8+(2).S3 in 6.Fi22.
So Lemma 2.3 (iii) yields two classes of O8+(2):S3 type
subgroups, which induce different permutation characters.
gap> s:= CharacterTable( "O8+(2).S3" );;
gap> s0:= CharacterTable( "O8+(2).3" );;
gap> CheckConditionsForLemma3( s0, s, facttbl, tbl, "all" );
6.Fi22: O8+(2).3.2 lifts to a direct product,
proved by squares in [ 1, 22, 28, 30, 46, 55, 76, 104, 131, 141, 215 ].
gap> derpos:= ClassPositionsOfDerivedSubgroup( s );;
gap> factfus:= GetFusionMap( tbl, facttbl );;
gap> ForAll( PossibleClassFusions( s, tbl ),
> map -> NecessarilyDifferentPermChars( map, factfus, derpos ) );
true
gap> VerifyCandidates( s, tbl, 0, faith[1], "all" );
G = 6.Fi22: point stabilizer O8+(2).3.2, ranks [ 14, 14 ]
[ "1a+351ab+3080a+13650a+13728b+19305ab+42120ab+45045a+48048c+61776cd",
"1a+351ab+3080a+13650a+13728a+19305ab+42120ab+45045a+48048b+61776ab" ]
Each subgroup of the type O8+(2):3 in 3.Fi22 lifts to a direct product
in 6.Fi22, which yields one action in each case;
since there are two different permutation characters already for 3.Fi22
(see Section 3.30),
we get two different permutation characters induced from O8+(2):3.
gap> VerifyCandidates( CharacterTable( "O8+(2).3" ), tbl, 0,
> Concatenation( faith[2], faith[3] ), "all" );
G = 6.Fi22: point stabilizer O8+(2).3, ranks [ 17, 25 ]
[ "1a+1001a+3080a+10725a+13650a+13728ab+27027ab+45045a+48048bc+50050a+96525ab+\
123552cd",
"1a+351ab+1001a+3080a+7722ab+10725a+13650a+13728ab+19305ab+42120ab+45045a+48\
048bc+50050a+54054ab+61776abcd" ]
Each subgroup of the type O8+(2):2 in 3.Fi22 lifts to a direct product
in 6.Fi22, which yields two actions; the permutation characters are
different by the argument used for O8+(2):S3.
gap> VerifyCandidates( CharacterTable( "O8+(2).2" ), tbl, 0, faith[4], "all" );
G = 6.Fi22: point stabilizer O8+(2).2, ranks [ 25, 25 ]
[ "1a+351ab+352a+429a+3080a+13650a+13728b+19305ab+27027ab+42120ab+45045a+48048\
ac+61776cd+75075a+96525ab+123200a+123552cd",
"1a+351ab+352a+429a+3080a+13650a+13728a+19305ab+27027ab+42120ab+45045a+48048\
ab+61776ab+75075a+96525ab+123200a+123552cd" ]
gap> CompareWithDatabase( "6.Fi22", faith );
(Note that the rank 17 permutation character above was missing in the first
version of [LM].)
3.33 G = 6.Fi22.2
The group 6.Fi22.2 that is printed in the ATLAS has three faithful
multiplicity-free permutation actions,
with point stabilizers of the types O8+(2):3 ×2
and 2F4(2) (twice).
gap> tbl2:= CharacterTable( "6.Fi22.2" );;
gap> faith:= FaithfulCandidates( tbl2, "Fi22.2" );;
6: subgroup $O_8^+(2):3 \times 2 \leq O_8^+(2):S_3 \times 2$, degree 741312 (
1 cand.)
16: subgroup ${^2F_4(2)^{\prime}}.2$, degree 21555072 (1 cand.)
Let M be a maximal subgroup of 6.Fi22.2 that maps to a subgroup of
the type O8+(2).S3 ×2 under the canonical epimorphism to
Fi22.2.
Then the conditions of Lemma 4.1 are satisfied
for the factor group
F of M modulo the normal subgroup of the type O8+(2):
Condition (a) follows from the discussion in Section 3.29.
The group M ∩6.Fi22 has the structure 6 ×O8+(2).S3
(see Section 3.32);
this implies that the corresponding index 2 subgroup of F
has the structure 6 ×S3, which is condition (b).
For condition (c), note that the generators of the two direct factors
of order 3 in the Sylow 3 subgroup of F
are inverted by suitable involutions in F, thus they are commutators
and hence the Sylow 3 subgroup lies in F′.
Moreover, we know that M contains subgroups of the type
O8+(2).3 ×2 that do not lie inside 6.Fi22 and
intersect the centre of 6.Fi22 trivially,
because the factor group 2.Fi22.2 contains subgroups of this type
with the analogous property (see Section 3.29),
and the preimages of these groups in 6.Fi22.2 are split extensions
of the normal subgroup of order 3 (see Section 3.32).
So we conclude F ≅ G72,22,
and by the above computations,
there is exactly one class of O8+(2).3 ×2 type subgroups
in 6.Fi22.2 that do not lie in 6.Fi22.
(Since there are O8+(2).3 ×2 type subgroups also inside 6.Fi22,
we must use "extending" as the last argument of VerifyCandidates.)
gap> s:= CharacterTable( "O8+(2).3" ) * CharacterTable( "Cyclic", 2 );;
gap> VerifyCandidates( s, tbl, tbl2, faith[6], "extending" );
G = 6.Fi22.2: point stabilizer O8+(2).3xC2, ranks [ 16 ]
[ "1a^++351ab+1001a^-+3080a^++7722ab+10725a^++13650a^++13728ab+19305ab+42120ab\
+45045a^++48048bc+50050a^++54054ab+61776abcd" ]
The subgroup of the type 6 ×2F4(2)′ of 6.Fi22 extends
to 6 ×2F4(2) in 6.Fi22.2, which contains two subgroups
of the type 2F4(2), by Lemma 2.3;
so we get two classes of such subgroups,
which induce the same permutation character.
gap> VerifyCandidates( CharacterTable( "2F4(2)" ), tbl, tbl2, faith[16], "all" );
G = 6.Fi22.2: point stabilizer 2F4(2)'.2, ranks [ 22 ]
[ "1a^++1001a^++1430a^++13650a^++19305ab+27027ab+30030a^++51975ab+133056a^{\\p\
m}+289575a^-+386100ab+400400ab+405405ab+579150a^++675675a^-+1201200a^-+1351350\
efgh+1663200ab+1796256abcd" ]
gap> faith[16]:= faith[16]{ [ 1, 1 ] };;
gap> CompareWithDatabase( "6.Fi22.2", faith );
The group (6.Fi22.2)∗ of the isoclinism type that is not printed
in the ATLAS has three faithful multiplicity-free permutation actions,
with point stabilizers of the type O8+(2):S3 (three times).
gap> facttbl:= CharacterTable( "Fi22.2" );;
gap> tbl2:= IsoclinicTable( tbl, tbl2, facttbl );;
gap> faith:= FaithfulCandidates( tbl2, "Fi22.2" );;
7: subgroup $O_8^+(2):S_3 \leq O_8^+(2):S_3 \times 2$, degree 741312 (
2 cand.)
The existence of O8+(2):S3 type subgroups not contained in 6.Fi22
follows from Lemma 2.2 and the existence of one class of these
subgroups in (2.Fi22.2)∗;
note that we get three complements of the normal subgroup of order 3
in each subgroup of the type 3.O8+(2):S3,
but Lemma 2.2 does not state anything about the G-conjugacy
of these groups.
So we argue as in the case of 6.Fi22.2,
and let M be a maximal subgroup of (6.Fi22.2)∗
that maps to a subgroup of the type O8+(2).S3 ×2
under the canonical epimorphism to Fi22.2.
As above, the conditions of Lemma 4.1 are satisfied
for the factor group
F of M modulo the normal subgroup of the type O8+(2).
This time, we conclude F ≅ G72,23,
so there are exactly three classes of O8+(2):S3 type subgroups
in (6.Fi22.2)∗ that do not lie in 6.Fi22.
Now the question remains how these three classes of point stabilizers
must be mapped to the two possible permutation characters
we found above.
For that,
we first note that by the last statement of Lemma 4.1,
the intersections of the point stabilizers with 6.Fi22
lie in two different conjugacy classes of O8+(2):3 type subgroups
of 6.Fi22.
These are the point stabilizers of the two multiplicity-free
permutation characters of degree 741 321 that have been established in
Section 3.32.
This means that the two possible permutation characters are indeed
permutation characters.
Which one belongs to two multiplicity-free actions of
(6.Fi22.2)∗?
Let us induce the trivial characters of the two relevant point stabilizers
in 6.Fi22 in two steps,
first to the maximal subgroup 6 ×O8+(2).S3 of 6.Fi22
and then from this group to 6.Fi22.
The two characters obtained in the first step have degree 12,
and the one whose extension to (6.Fi22.2)∗ belongs to two actions
is induced from a non-normal O8+(2).3 type subgroup
of 6 ×O8+(2).S3,
whereas the other character is induced from a normal (but noncentral)
subgroup of this type.
We execute the first step in the factor group of the type 6 ×S3,
then inflate the degree 12 characters to 6 ×O8+(2).S3,
and finally induce the these characters to 6.Fi22.
gap> s:= CharacterTable( "O8+(2).S3" ) * CharacterTable( "Cyclic", 6 );;
gap> fact:= s / ClassPositionsOfSolvableResiduum( s );;
gap> Size( fact );
36
gap> OrdersClassRepresentatives( fact );
[ 1, 6, 3, 2, 3, 6, 3, 6, 3, 6, 3, 6, 2, 6, 6, 2, 6, 6 ]
gap> SizesCentralizers( fact );
[ 36, 36, 36, 36, 36, 36, 18, 18, 18, 18, 18, 18, 12, 12, 12, 12, 12, 12 ]
gap> ind:= InducedCyclic( fact, [ 7, 9, 11 ] );;
gap> List( ind, ValuesOfClassFunction );
[ [ 12, 0, 0, 0, 0, 0, 0, 0, 6, 0, 6, 0, 0, 0, 0, 0, 0, 0 ],
[ 12, 0, 0, 0, 0, 0, 12, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ] ]
(The first character has a trivial kernel,
so it is the one that is induced from a non-normal subgroup of order three.)
gap> rest:= RestrictedClassFunctions( ind, s );;
gap> fus:= PossibleClassFusions( s, tbl );;
gap> Length( fus );
4
gap> ind:= Set( List( fus, map -> Induced( s, tbl, rest, map ) ) );;
gap> Length( ind );
1
gap> rest:= RestrictedClassFunctions( faith[7], tbl );;
gap> List( ind[1], pi -> Position( rest, pi ) );
[ 1, 2 ]
So the induced characters are uniquely determined,
and the first of the two characters in faith[7] is afforded by two
multiplicity-free actions of (6.Fi22.2)∗.
gap> s:= CharacterTable( "O8+(2).S3" );;
gap> VerifyCandidates( s, tbl, tbl2, faith[7], "extending" );
G = Isoclinic(6.Fi22.2): point stabilizer O8+(2).3.2, ranks [ 12, 16 ]
[ "1a^++1001a^++3080a^++10725a^-+13650a^++13728ab+27027ab+45045a^++48048bc+500\
50a^-+96525ab+123552cd",
"1a^++351ab+1001a^++3080a^++7722ab+10725a^-+13650a^++13728ab+19305ab+42120ab\
+45045a^++48048bc+50050a^-+54054ab+61776abcd" ]
gap> faith[7]:= faith[7]{ [ 1, 1, 2 ] };;
gap> CompareWithDatabase( "Isoclinic(6.Fi22.2)", faith );
3.34 G = 2.Co1
The group 2.Co1 has two faithful multiplicity-free permutation actions,
with point stabilizers of the types Co2 and Co3,
respectively, by Lemma 2.1.
gap> tbl:= CharacterTable( "2.Co1" );;
gap> faith:= FaithfulCandidates( tbl, "Co1" );;
1: subgroup $Co_2$, degree 196560 (1 cand.)
5: subgroup $Co_3$, degree 16773120 (1 cand.)
gap> VerifyCandidates( CharacterTable( "Co2" ), tbl, 0, faith[1], "all" );
G = 2.Co1: point stabilizer Co2, ranks [ 7 ]
[ "1a+24a+299a+2576a+17250a+80730a+95680a" ]
gap> VerifyCandidates( CharacterTable( "Co3" ), tbl, 0, faith[5], "all" );
G = 2.Co1: point stabilizer Co3, ranks [ 12 ]
[ "1a+24a+299a+2576a+17250a+80730a+95680a+376740a+1841840a+2417415a+5494125a+6\
446440a" ]
gap> CompareWithDatabase( "2.Co1", faith );
3.35 G = 3.F3+
The group 3.F3+ has two faithful multiplicity-free permutation actions,
with point stabilizers of the types Fi23 and O10−(2),
respectively, by Lemma 2.1.
gap> tbl:= CharacterTable( "3.F3+" );;
gap> faith:= FaithfulCandidates( tbl, "F3+" );;
1: subgroup $Fi_{23}$, degree 920808 (1 cand.)
2: subgroup $O_{10}^-(2)$, degree 150532080426 (1 cand.)
gap> VerifyCandidates( CharacterTable( "Fi23" ), tbl, 0, faith[1], "all" );
G = 3.F3+: point stabilizer Fi23, ranks [ 7 ]
[ "1a+783ab+57477a+249458a+306153ab" ]
gap> VerifyCandidates( CharacterTable( "O10-(2)" ), tbl, 0, faith[2], "all" );
G = 3.F3+: point stabilizer O10-(2), ranks [ 43 ]
[ "1a+783ab+8671a+57477a+64584ab+249458a+306153ab+555611a+1666833a+6724809ab+1\
9034730ab+35873145a+43779879ab+48893768a+79452373a+195019461ab+203843871ab+415\
098112a+1050717096ab+1264015025a+1540153692a+1818548820ab+2346900864a+32086535\
25a+10169903744a+10726070355ab+13904165275a+15016498497ab+17161712568a+2109675\
1104ab" ]
gap> CompareWithDatabase( "3.F3+", faith );
3.36 G = 3.F3+.2
The group 3.F3+.2 has two faithful multiplicity-free permutation actions,
with point stabilizers of the types Fi23 ×2 and O10−(2).2,
respectively, by Lemma 2.2.
gap> tbl2:= CharacterTable( "3.F3+.2" );;
gap> faith:= FaithfulCandidates( tbl2, "F3+.2" );;
1: subgroup $Fi_{23} \times 2$, degree 920808 (1 cand.)
3: subgroup $O_{10}^-(2).2$, degree 150532080426 (1 cand.)
gap> VerifyCandidates( CharacterTable( "2xFi23" ), tbl, tbl2, faith[1], "all" );
G = 3.F3+.2: point stabilizer 2xFi23, ranks [ 5 ]
[ "1a^++783ab+57477a^++249458a^++306153ab" ]
gap> VerifyCandidates( CharacterTable( "O10-(2).2" ), tbl, tbl2, faith[3], "all" );
G = 3.F3+.2: point stabilizer O10-(2).2, ranks [ 30 ]
[ "1a^++783ab+8671a^-+57477a^++64584ab+249458a^++306153ab+555611a^-+1666833a^+\
+6724809ab+19034730ab+35873145a^++43779879ab+48893768a^-+79452373a^++195019461\
ab+203843871ab+415098112a^-+1050717096ab+1264015025a^++1540153692a^++181854882\
0ab+2346900864a^-+3208653525a^++10169903744a^-+10726070355ab+13904165275a^++15\
016498497ab+17161712568a^++21096751104ab" ]
gap> CompareWithDatabase( "3.F3+.2", faith );
The group 2.B has one faithful multiplicity-free permutation action,
with point stabilizer of the type Fi23, by Lemma 2.1.
gap> tbl:= CharacterTable( "2.B" );;
gap> faith:= FaithfulCandidates( tbl, "B" );;
4: subgroup $Fi_{23}$, degree 2031941058560000 (1 cand.)
gap> VerifyCandidates( CharacterTable( "Fi23" ), tbl, 0, faith[4], "all" );
G = 2.B: point stabilizer Fi23, ranks [ 34 ]
[ "1a+4371a+96255a+96256a+9458750a+10506240a+63532485a+347643114a+356054375a+4\
10132480a+4221380670a+4275362520a+8844386304a+9287037474a+13508418144a+3665765\
3760a+108348770530a+309720864375a+635966233056a+864538761216a+1095935366250a+4\
322693806080a+6145833622500a+6619124890560a+10177847623680a+12927978301875a+38\
348970335820a+60780833777664a+89626740328125a+110949141022720a+211069033500000\
a+284415522641250b+364635285437500a+828829551513600a" ]
gap> CompareWithDatabase( "2.B", faith );
4 Appendix: Explicit Computations with Groups
Only in the proofs for the groups involving M22, explicit computations
with the groups were necessary to determine multiplicity-free permutation
characters.
Additionally, the structure of certain small factor groups
of maximal subgroups in extension of Fi22 had to be analyzed
in order to determine the multiplicity of actions whose existence had been
established character-theoretically.
These computations are collected in this appendix.
4.1 24:A6 type subgroups in 2.M22
We show that the preimage in 2.M22 of each maximal subgroup of the type
24:A6 in M22 contains one class of subgroups of the type
2 ×24:A5.
For that, we first note that there are two classes of subgroups of the type
24:A5 inside 24:A6, and that the A5 subgroups lift to groups
of the type 2 ×A5 because 2.M22 does not admit an embedding of
2.A6.
gap> tbl:= CharacterTable( "2.M22" );;
gap> PossibleClassFusions( CharacterTable( "2.A6" ), tbl );
[ ]
Now we fetch a permutation representation of 2.M22 on 352 points,
from the ATLAS of Group Representations (see [WWT+]),
via the GAP package AtlasRep (see [WPN+22]),
and compute generators for the second class of maximal subgroups,
via the straight line program for M22.
gap> info:= OneAtlasGeneratingSetInfo( "2.M22", NrMovedPoints, 352 );;
gap> gens:= AtlasGenerators( info.identifier );;
gap> slp:= AtlasStraightLineProgram( "M22", "maxes", 2 );;
gap> sgens:= ResultOfStraightLineProgram( slp.program, gens.generators );;
gap> s:= Group( sgens );; Size( s );
11520
gap> 2^5 * 360;
11520
The subgroup acts intransitively on the 352 points.
We switch to the faithful representation on 192 points,
and compute the normal subgroup N of order 25.
gap> orbs:= Orbits( s, MovedPoints( s ) );;
gap> List( orbs, Length );
[ 160, 192 ]
gap> s:= Action( s, orbs[2] );;
gap> Size( s );
11520
gap> syl2:= SylowSubgroup( s, 2 );;
gap> repeat
> x:= Random( syl2 );
> n:= NormalClosure( s, SubgroupNC( s, [ x ] ) );
> until Size( n ) = 32;
The point stabilizer S in this group has type A5,
and generates together with N one of the desired subgroups of the type
25:A5.
However, S does not normalize a subgroup of order 24,
and so there is no subgroup of the type 24:A5.
gap> stab:= Stabilizer( s, 192 );;
gap> sub:= ClosureGroup( n, stab );;
gap> Size( sub );
1920
gap> Set( List( Elements( n ),
> x -> Size( NormalClosure( sub, SubgroupNC( sub, [ x ] ) ) ) ) );
[ 1, 2, 32 ]
A representative of the other class of A5 type subgroups can be found
by taking an element x of order three that is not conjugate to one in S,
and to choose an element y of order five such that the product is an
involution.
gap> syl3:= SylowSubgroup( s, 3 );;
gap> repeat three:= Random( stab ); until Order( three ) = 3;
gap> repeat other:= Random( syl3 );
> until Order( other ) = 3 and not IsConjugate( s, three, other );
gap> syl5:= SylowSubgroup( s, 5 );;
gap> repeat y:= Random( syl5 )^Random( s ); until Order( other*y ) = 2;
gap> a5:= Group( other, y );;
gap> IsConjugate( s, a5, stab );
false
gap> sub:= ClosureGroup( n, a5 );;
gap> Size( sub );
1920
gap> Set( List( Elements( n ),
> x -> Size( NormalClosure( sub, SubgroupNC( sub, [ x ] ) ) ) ) );
[ 1, 2, 16, 32 ]
This proves the existence of one class of the desired subgroups.
Finally, we show that the character table of these groups is indeed
the one we used in Section 3.3.
gap> g:= First( Elements( n ),
> x -> Size( NormalClosure( sub, SubgroupNC( sub, [ x ] ) ) ) = 16 );;
gap> compl:= ClosureGroup( a5, g );;
gap> Size( compl );
960
gap> tbl:= CharacterTable( compl );;
gap> IsRecord( TransformingPermutationsCharacterTables( tbl,
> CharacterTable( "P1/G1/L1/V1/ext2" ) ) );
true
4.2 24:S5 type subgroups in M22.2
A maximal subgroup of the type 24:S6 in M22.2 is perhaps easiest
found as the point stabilizer in the degree 77 permutation representation.
In order to find its index 6 subgroups,
the degree 22 permutation representation of M22.2 is more suitable
because the restriction to the 24:S6 type subgroup has orbits of the
lengths 6 and 16, where the action of the orbit of length 6 is the
natural permutation action of S6.
So we choose the sum of the two representations, of total degree 99.
For convenience, we find this representation as the point stabilizer in the
degree 100 representation of HS.2, which is contained in the ATLAS
of Group Representations (see [WWT+]).
gap> info:= OneAtlasGeneratingSetInfo( "HS.2", NrMovedPoints, 100 );;
gap> gens:= AtlasGenerators( info.identifier );;
gap> stab:= Stabilizer( Group( gens.generators ), 100 );;
gap> orbs:= Orbits( stab, MovedPoints( stab ) );;
gap> List( orbs, Length );
[ 77, 22 ]
gap> pnt:= First( orbs, x -> Length( x ) = 77 )[1];;
gap> m:= Stabilizer( stab, pnt );;
gap> Size( m );
11520
Now we find two nonconjugate subgroups of the type 24:S5 as the stabilizer
of a point and of a total in S6, respectively (cf. [CCN+85,p. 4]).
gap> orbs:= Orbits( m, MovedPoints( m ) );;
gap> List( orbs, Length );
[ 60, 16, 6, 16 ]
gap> six:= First( orbs, x -> Length( x ) = 6 );;
gap> p:= ( six[1], six[2] )( six[3], six[4] )( six[5], six[6] );;
gap> conj:= ( six[2], six[4], six[5], six[6], six[3] );;
gap> total:= List( [ 0 .. 4 ], i -> p^( conj^i ) );;
gap> stab1:= Stabilizer( m, six[1] );;
gap> stab2:= Stabilizer( m, Set( total ), OnSets );;
gap> IsConjugate( m, stab1, stab2 );
false
We identify the character tables of the two groups in the GAP Character
Table Library.
gap> s1:= CharacterTable( stab1 );;
gap> s2:= CharacterTable( stab2 );;
gap> NrConjugacyClasses( s1 ); NrConjugacyClasses( s2 );
12
18
gap> lib1:= CharacterTable( "2^4:s5" );;
gap> IsRecord( TransformingPermutationsCharacterTables( lib1, s1 ) );
true
gap> lib2:= CharacterTable( "w(d5)" );;
gap> IsRecord( TransformingPermutationsCharacterTables( lib2, s2 ) );
true
The first subgroup does not lead to multiplicity-free permutation characters
of 2.M22.2.
Note that there are two classes of subgroups of this type in M22.2,
one of them is contained in M22 and the other is not.
The action on the cosets of the former is multiplicity-free,
but it does not lift to a multiplicity-free candidate of 2.M22.2;
and the action on the cosets of the latter is not multiplicity-free.
gap> tbl:= CharacterTable( "M22" );;
gap> tbl2:= CharacterTable( "M22.2" );;
gap> pi:= PossiblePermutationCharacters( s1, tbl2 );
[ Character( CharacterTable( "M22.2" ),
[ 462, 30, 12, 2, 2, 2, 0, 0, 0, 0, 0, 56, 0, 0, 12, 2, 2, 0, 0, 0, 0 ] ),
Character( CharacterTable( "M22.2" ),
[ 462, 46, 12, 6, 6, 2, 4, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ] ) ]
gap> PermCharInfoRelative( tbl, tbl2, pi ).ATLAS;
[ "1a^++21(a^+)^{2}+55a^++154a^++210a^+",
"1a^{\\pm}+21a^{\\pm}+55a^{\\pm}+154a^{\\pm}" ]
So only the second type of 24:S5 type subgroups can lift to the
multiplicity-free candidate in question,
and this situation is dealt with in Section 3.4.
gap> pi:= PossiblePermutationCharacters( s2, tbl2 );
[ Character( CharacterTable( "M22.2" ),
[ 462, 30, 3, 2, 2, 2, 3, 0, 0, 0, 0, 28, 20, 4, 8, 1, 2, 0, 1, 0, 0 ] ) ]
gap> PermCharInfoRelative( tbl, tbl2, pi ).ATLAS;
[ "1a^++21a^++55a^++154a^++231a^-" ]
4.3 Multiplicities of Multiplicity-Free Actions of 6.Fi22.2
We collect the information used in Section 3.33 in a lemma.
Lemma 1
Up to isomorphism, there are exactly two groups G of order 72
with the following properties:
(a)
the Sylow 2 subgroup of G is a dihedral group,
(b)
G has a normal subgroup isomorphic to 6 ×S3, and
(c)
G/G′ is a 2-group.
In the GAP library of small groups, they have the identifiers
[ 72, 22 ] and [ 72, 23 ].
Let us denote these groups by G72,22 and G72,23,
let G be one of them, and let N be any normal subgroup of G that
satisfies condition (b).
If G = G72,22 then there is exactly one conjugacy class of cyclic
subgroups of order 6 in G that have trivial intersection with Z(N);
if G = G72,23 then there are no such subgroups in G.
If G = G72,23 then there are exactly three conjugacy classes of
nonabelian subgroups of order 6 in G that do not lie in N and
have trivial intersection with Z(N);
if G = G72,22 then there are no such subgroups in G.
Let U1, U2, U3 denote representatives of the three classes of
nonabelian subgroups of order 6 in G72,23 mentioned above;
the Sylow 3 subgroups of these groups are pairwise different,
one of them is normal in N and the other two are conjugate in N.
The proof is given by the following calculations using GAP.
We use the classification of groups of order 72,
which had been obtained in [Neu67].
The groups are available in GAP via the database of small groups,
see [BE99].
gap> id_d8:= IdGroup( DihedralGroup( 8 ) );;
gap> id_2xs3:= IdGroup( DirectProduct( CyclicGroup(2), SymmetricGroup(3) ) );;
gap> id_6xs3:= IdGroup( DirectProduct( CyclicGroup(6), SymmetricGroup(3) ) );;
gap> grps:= AllSmallGroups( Size, 72,
> g -> IdGroup( SylowSubgroup( g, 2 ) ) = id_d8 and
> ForAny( NormalSubgroups( g ),
> n -> IdGroup( n ) = id_6xs3 ) and
> ForAll( AbelianInvariants(g), IsEvenInt ), true );
[ <pc group of size 72 with 5 generators>,
<pc group of size 72 with 5 generators> ]
gap> List( grps, IdGroup );
[ [ 72, 22 ], [ 72, 23 ] ]
gap> is_good_1:= function( R, N )
> return Size( R ) = 6 and IsCyclic( R ) and
> Size( Intersection( R, Centre( N ) ) ) = 1;
> end;;
gap> is_good_2:= function( R, N )
> return Size( R ) = 6 and not IsCyclic( R ) and
> not IsSubset( N, R ) and
> Size( Intersection( R, Centre( N ) ) ) = 1;
> end;;
gap> cand:= Filtered( NormalSubgroups( grps[1] ),
> n -> IdGroup( n ) = id_6xs3 );;
gap> classreps:= List( ConjugacyClassesSubgroups( grps[1] ),
> Representative );;
gap> List( cand, N -> Number( classreps, R -> is_good_1( R, N ) ) );
[ 1, 1 ]
gap> List( cand, N -> Number( classreps, R -> is_good_2( R, N ) ) );
[ 0, 0 ]
gap> cand:= Filtered( NormalSubgroups( grps[2] ),
> n -> IdGroup( n ) = id_6xs3 );;
gap> classreps:= List( ConjugacyClassesSubgroups( grps[2] ),
> Representative );;
gap> List( cand, N -> Number( classreps, R -> is_good_1( R, N ) ) );
[ 0 ]
gap> List( cand, N -> Number( classreps, R -> is_good_2( R, N ) ) );
[ 3 ]
gap> N:= cand[1];;
gap> subs:= Filtered( classreps, R -> is_good_2( R, N ) );;
gap> syl3:= List( subs, x -> SylowSubgroup( x, 3 ) );;
gap> Length( Set( syl3 ) );
3
gap> Number( syl3, x -> IsNormal( N, x ) );
1
References
- [BE99]
-
H. U. Besche and B. Eick, The groups of order at most 1000 except 512 and
768, J. Symbolic Comput. 27 (1999), no. 4, 405-413.
MR 1681347 (2000c:20002)
- [BL96]
-
T. Breuer and K. Lux, The multiplicity-free permutation characters of the
sporadic simple groups and their automorphism groups, Comm. Algebra
24 (1996), no. 7, 2293-2316. MR 1390375 (97c:20020)
- [BM05]
-
T. Breuer and J. Müller, Character tables of endomorphism rings of
multiplicity-free permutation modules of the sporadic
simple groups and their cyclic and bicyclic extensions, https://www.math.rwth-aachen.de/
~Juergen.Mueller/
mferctbl/mferctbl.html, 2005.
- [Bre25]
-
T. Breuer, The GAP Character Table Library, Version
1.3.10, https://www.math.rwth-aachen.de/
~Thomas.Breuer/
ctbllib, May 2025, GAP package.
- [CCN+85]
-
J. H. Conway, R. T. Curtis, S. P. Norton, R. A. Parker, and R. A. Wilson,
Atlas of finite groups, Oxford University Press, Eynsham, 1985,
Maximal subgroups and ordinary characters for simple groups, With
computational assistance from J. G. Thackray. MR 827219 (88g:20025)
- [GAP24]
-
GAP - Groups, Algorithms, and Programming,
Version 4.13.1, https://www.gap-system.org, Mar 2024.
- [Höh01]
-
I. Höhler, Vielfachheitsfreie Permutationsdarstellungen und die
Invarianten zugehöriger Graphen, Examensarbeit, Lehrstuhl D für
Mathematik, Rheinisch Westfälische Technische Hochschule, Aachen,
Germany, 2001.
- [LM]
-
S. A. Linton and S. A. Mpono, Multiplicity-free
permutation characters of covering groups of sporadic simple groups,
preprint.
- [Mül03]
-
J. Müller, On endomorphism rings and character tables,
Habilitationsschrift, Lehrstuhl D für Mathematik, Rheinisch
Westfälische Technische Hochschule, Aachen, Germany, 2003.
- [Mül08]
-
, On the multiplicity-free actions of the
sporadic simple groups, J. Algebra 320 (2008), no. 2,
910-926. MR 2422321 (2009d:20028)
- [Neu67]
-
J. Neubüser, Die Untergruppenverbände der Gruppen der
Ordnungen ≤ 100 mit Ausnahme der Ordnungen 64 und 96,
Habilitationsschrift, Universität Kiel, Kiel, Germany, 1967.
- [WPN+22]
-
R. A. Wilson, R. A. Parker, S. Nickerson, J. N. Bray, and T. Breuer,
AtlasRep, a GAP Interface to the Atlas of Group
Representations, Version 2.1.6, https://www.math.rwth-aachen.de/
~Thomas.Breuer/
atlasrep, Oct 2022, GAP package.
- [WWT+]
-
R. A. Wilson, P. Walsh, J. Tripp, I. Suleiman, R. A. Parker, S. P. Norton,
S. Nickerson, S. Linton, J. Bray, and R. Abbott, ATLAS of Finite Group
Representations, http://brauer.maths.qmul.ac.uk/
Atlas/.
File translated from
TEX
by
TTH,
version 3.59.
On 22 May 2025, 15:04.

