§ 1 Figurierte Zahlen: Anschauung und Kreativität

1. Finden sie eine Formel für Δ_n = Summe der ersten n natürlichen Zahlen!

( z.B. 1 + 2 + ... + )

Idee: Die Summe der letzten und der ersten Zahl der gegebenen Summe ergibt , die Summe der vorletzten und der zweiten Zahl ergibt wieder , u.s.w..

Insgesamt ergeben sich solcher Paare.

→ Δ_n =

Anschauung: Mit Hilfe von Kästchen lassen sich die Zahlen von 1 .. n darstellen: Die erste Spalte des 'Dreiecks' stellt die Zahl 1 dar, die zweite Spalte die Zahl 2, u.s.w..

Die Summe der gesamten Kästchen ergibt nun Δ_{n .}

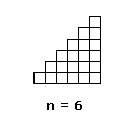
Bilde also durch Übereinanderlegen zweier Dreicks-Kästchen- Formen ein Rechteck: Es entsteht ein Rechteck mit den Seitenlängen n und n+1.

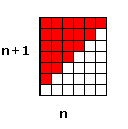
→ Formel:

2. Finden sie eine Formel für U_n := Summe der ersten n ungeraden natürlichen Zahlen!

Plan: 0) Tabelle von Beispielen zur Aufstellung einer Vermutung

1) Behauptung formulieren

2) Behauptung beweisen

Schreiben:

0)

1) Behauptung: U_n := n².

2) Beweis per vollständiger Induktion:

Da wir die Summe der ungeraden Zahlen berechnen, ist

Damit ist: n = 1 √

Induktionsschritt:

√

Damit haben wir nach dem Induktionsprinzip unsere Vermutung bewiesen (aber noch lange nicht verstanden)!

3) Anschauliche Vorstellungen:

(i) Stelle die Zahlen erneut durch Kästchen dar. Die erste Spalte in weiß gehört zu n=1, die zweite zu n=2 ... Da nur die ungeraden Zahlen summiert werden sollen, sind als n-te Spalte 2n-1 Kästchen gezeichnet. Legt man nun das 'Dreieck' noch einmal oben dran (rot), erhält man ein Rechteck der Seitenlängen n und (2n-1)+1.

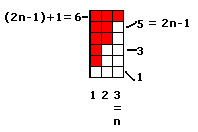
→ Formel:

(ii) Eine weitere Idee ist, die Kästchen entsprechend den Zahlen direkt zu einem Quadrat zu legen. Jede größere, ungerade Zahl ergibt ein größeres Quadrat.

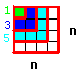
Dies ergibt ein Quadrat mit der Seitenlänge n. →

3. Finden sie eine Formel für A_n := 1+2+3+..+(n-1)+n+(n-1)..+1 (Auf-und-Ab-Regel)!

Methode: Bekannte Formel anweden:

Drücke also A_n durch Δ_n aus.

Anschauliche Vorstellung: Wie im ersten Beispiel bilden wir wieder ein Rechteck durch übereinanderlegen zweier 'Dreiecke', mit dem Unterschied, dass wir nun (da der zweite Teil der Summe A_n nur bis (n-1) geht) die Spalte für n weg lassen. Es ergibt sich also ein Quadrat der Seitenlänge n.

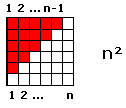
→ A_n = n²

4. Finden sie eine Formel für Q_n := Summe der ersten n Quadrate!

Plan: 0) Gewinnung einer Vermutung

Methoden: a)Beispiele hinschreiben

b)Geometrische Idee

Zu a) Betrachte die Summe der Quadrate genauer: Auffällig ist, dass der Abstand zweier aufeinanderfolgender Summanden gerade die ungeraden Zahlen darstellen.

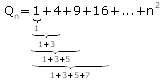
Benutze also U_n=1+3+5+7+... →

(nicht weiter verfolgt)

Zu b) Benutze schon bekannte Summen:

Bilde für die Summe Q_n ein Dreieck folgender Form (hier für n=4):

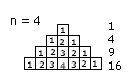
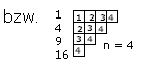
Setzte das zweite Dreieck nun zweimal an das erste an und erhalte einen „Pfeil“, der auf zwei unterschiedliche Art und Weisen interpretiert werden kann:

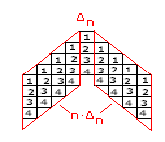
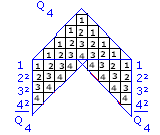
Also:

5. Finden sie eine Formel für K_n := Summe der ersten n Kuben!

Methode: Bekannte Formel anwenden:

Wie in Teil 1) ist Δ_n anschaulich:

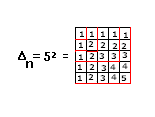
Multipliziert man zwei solcher Δ_n so erhält man die anschauliche Darstellung von K_n :

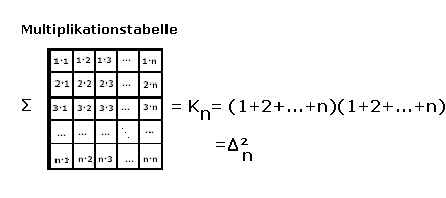
Damit: K_n=