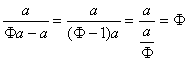Elementare Zahlentheorie WS 2003/04
![]()
Protokoll 22.01.2004 (AZ)
§ 9 B:
Der Goldene Schnitt (EB)
Frage: Was ist der Goldene Schnitt?
Definition:
![]() sei eine Strecke. Ein Punkt S auf der Strecke
sei eine Strecke. Ein Punkt S auf der Strecke
![]() teilt
teilt
![]() im Goldenen Schnitt, falls sich die größere Teilstrecke zur kleineren so verhält
wie die Gesamtstrecke zur größeren Teilstrecke.
im Goldenen Schnitt, falls sich die größere Teilstrecke zur kleineren so verhält
wie die Gesamtstrecke zur größeren Teilstrecke.
Dabei gibt es immer zwei Möglichkeiten für den Schnitt, nämlich eine von links und eine von rechts.
Sei
![]() eine Strecke der Länge a. Ein Punkt S auf
eine Strecke der Länge a. Ein Punkt S auf
![]() teilt die Strecke im Goldenen Schnitt, falls
teilt die Strecke im Goldenen Schnitt, falls
![]() das heißt genau dann, wenn M2 = am.
das heißt genau dann, wenn M2 = am.
Behauptung: Genau dann teilt ein Punkt S die Strecke
![]() im Goldenen Schnitt, wenn
im Goldenen Schnitt, wenn
![]() ist.
ist.
Beispiele aus der Kunst zeigen, dass der Goldene Schnitt in Kunst und Architektur sehr bedeutend ist. Man will nicht alles zentrieren, um Bilder und Bauwerke interessanter zu machen. Außerdem wird das Auge gerade von Dingen angezogen, die nicht mittig sind.






Beweis der Behauptung:
|
![]() | = a , also a = M + m
| = a , also a = M + m
zu zeigen:
![]()
dazu: M² = am
M² = (M + m)m = Mm + m²
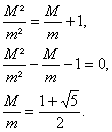
Da die negative Lösung nicht möglich ist, ergibt sich
![]() .
.
Ein alternativer Beweis ist:
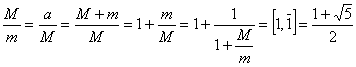 .
.
Wir bezeichnen nun
![]() .
.
Charakteristische Eigenschaften von
![]() :
:
(1)
![]() ² =
² =
![]() +1
+1
(2)
![]() =
=
![]() -1
-1
(3)
![]() +
+
![]() =
=
![]()
Beweis zur Konstruktion1:
Zu zeigen:
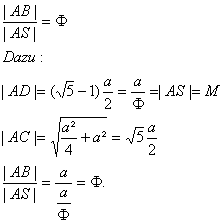
Beweis zur Konstruktion 4:
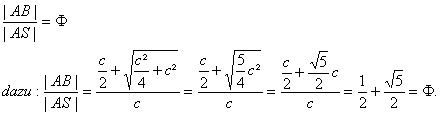
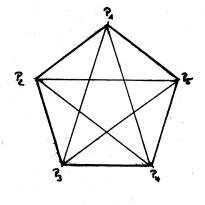
Das Verhältnis einer Diagonalen zu einer Seite ist ein Goldener Schnitt.
Das Goldene Dreieck:
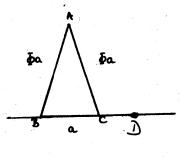
Das Verhältnis der Schenkel zur Basis ist gleich
![]() .
.
Frage: Wie kann man aus einer Strecke ein Goldenes Dreieck konstruieren?
Man geht von der Basis als vorgegebene Strecke aus. Dann
konstruiert man einen weiteren Punkt
![]() a wie in Konstruktion 4. Dann zieht man um die Eckpunkte der Basis einen Kreis
mit Radius
a wie in Konstruktion 4. Dann zieht man um die Eckpunkte der Basis einen Kreis
mit Radius
![]() a.
a.
Das Goldene Rechteck:
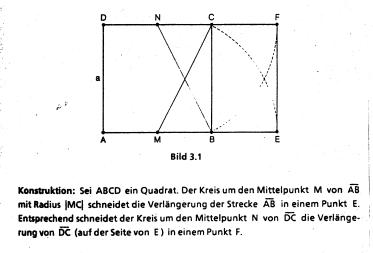
Die Goldene Spirale:
Die Goldene Spirale entsteht, indem man ein Goldenes Rechteck in ein Quadrat und ein neues Goldenes Rechteck aufteilt, das man dann wieder aufteilt und so weiter.
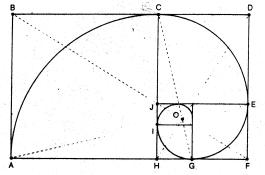
Beweis, dass das kleinere Dreieck wieder Golden ist: