[Zur vorangehenden Stunde (23.01.04),
zur nächsten Stunde (29.01.04),
zur Protokollübersicht]

Quadratische Gleichungen und iterative Lösungen

Inhalt: § 9 D: Vergleich mit Heron-Verfahren (SM + AZ)

Betrachte folgendes Rechteck:

x

Fläche = 14 = x * y   1/2 * Umfang = 8 = x + y

Gesucht ist nun eine Lösung für (x, y), wobei iterativ vorgegangen werden soll (d.h. keine Benutzung der p/q-Formel).

Folgende Idee: Man gibt sich einen Wert in einer Formel beliebig vor, damit berechnet man den zweiten Wert aus. Diesen setzt man in die erst Formel ein und erhält einen neuen Wert für die erste Variable. Diese setzt man nun wieder in die andere Formel ein usw.:

Gebe in der Umfangsformel x₁ = 3 vor:

Betrachten wir also noch einmal die Formeln:

,

und den Graphen von f(x):

Hier sieht man das Verfahren graphisch verdeutlicht. Die orangen Striche markieren dabei gerade die jeweils neuen x -Werte.

Führen wir zuletzt die Sache auf eine verallgemeinerte Kettenbruchentwicklung zurück:

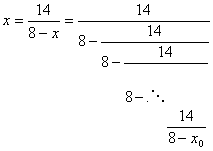
Wenn man sich den Graphen genauer ansieht, sieht man eine Symmetrie der beiden Lösungen (Punktspiegelung an (4,0)). Also verschieben wir die Funktion so, so dass (4,0) in den Ursprung kommt.

D.h. für
-b = x * y
a = y - x
=> -b = x * (x +a)
gilt:

 

allgemein x * (x + a) = -b Setze z := x + a/ 2 (z - a/2) * (z + a/2) = b z2 - a2/4 = -b =>

bei uns 14 = x * (8 - x) Setze z := x - 4 14 = (z + 4) * (4 - z) 14 = 16 - z2

Nun zum zweiten Teil der Vorlesung:

Berechnung von Wurzeln, speziell Lösung zu x² = 2

Das HERON-Verfahren

 F: Wie kann man (Quadrat-)Wurzeln berechnen?

1) Geometrischer Zugang:

x

a ist der Flächeninhalt des Rechtecks. Dann gilt: x' = (x + y) / 2 und y' = 2a / (x + y).

                    y = a / x

2) Arithmetischer Zugang:

1. Abschätzung von . Man erhält y.
x < < y oder x > > y.

2. Bildung des arithmetischen Mittels:

x' = 1/2 * (x + a/x)

3. Abschätzung zwischen artihmetischem und geometrischem Mittel:

4. Rekursionsfortschritt:

x₀ > 0 beliebig,

x_{n + 1} = 1/2 (x_n + a/x_n)

Satz: Für jeden Startwert x₀ > 0 konvergiert die Folge des Heronverfahrens gegen .

Beweis: [Z.z.: 1) x_n > und 2) x_n > x_n+1]

Ad 1): Siehe 3. mit x' := x_n und x := x_{n - 1}.

Ad 2): Aus x_n > folgt a/x_n < , also x_n > a/x_n, und x_{n + 1} ist das arithmetische Mittel von x_n und y_n. Deswegen folgt: x_n > x_{n + 1}. [Also ist die Folge streng monoton fallend und nach unten beschränkt, also konvergiert sie.] Bleibt nur noch zu zeigen, gegen welchen Wert sie konvergiert.

Beh.: ist der Grenzwert.

Bew.: Es sei z der Grenzwert. Aus 1) folgt, dass z ≥ > 0 ist. Also folgt aus x_n+1 = 1/2 (x_n + a/x_n), z = 1/2 (z + a/z). Daraus folgt nach Auflösen nach z die Behauptung. ||

Frage nun: Wie groß ist der Fehler?

Nach n Schritten gilt:

x_{n + 1} - = 1/(2*x_n) (x_n - )² . Man spricht in diesem Falle auch von quadratischer Konvergenz.

Satz: Die Anzahl der signifikanten Nachkommastellen verdoppelt sich bei jedem Schritt.

Beweis: Es sei a > 1. Es seien x_n und a/x_n in s Nachkommastellen genau, dann ist x_n - < 10^-s.
Also x_n+1 - = 1/(2 * x_n) (x_n - )² < 1/2 * 10^-2s.||