Elementare Zahlentheorie WS 2003/04

Stundenprotokoll von Freitag, dem 31.10.2003 (MH)

Thema: Restklassenringe

(Menge aller „Töpfe“)

1. Frage: Algebraische Struktur?

2. Frage: Anzahl der Elemente?

3. Frage: Erzeugendensystem?

Ad 1.:

Die algebraische Struktur dieser Menge ist ein kommutativer Ring-mit-1. Es bleibt die Frage zu beantworten, ob man auch mit den „Töpfen“ rechnen kann.

Wohldefiniert.

Wohldefiniert.

Auch das Inverse ist wohldefiniert.

Alle Gesetze, wie z.B. das Assoziativgesetz, sind erfüllt, da sie auch in gelten.

Es handelt sich bei der Menge um eine additive Struktur: kommutative Gruppe.

Insbesondere additiv geschrieben ab jetzt.

Ad 2.:

.

, d.h. dass die Gruppe n Elemente hat ().

Ad 3.:

Es ist die Frage zu klären, ob ein Element zur Erzeugung der Gruppe reichen würde? Wie sähe das Erzeugnis eines einzigen Elementes aus?

Unsere Überlegung geht dahin, dass die „1“ als Erzeuger in Frage kommt, und dann wäre das Erzeugnis die Menge aller Vielfachen von „1“. Jedoch kommt schnell die Frage nach der Erzeugung der „0“ durch die „1“. Ist die Erzeugung der „0“ möglich, wenn nur die „1“ voranden ist?

Unsere Antwort lautet, dass auch der „Nulltopf “ als Vielfaches von „1“ darstellbar ist: .

Wir stellen fest: , das heißt, der „Eins-Topf “ wird so oft addiert, wie es das x angibt, wenn x eine natürliche Zahl oder 0 ist. Wenn es negativ ist, so wird ein „-“ - Zeichen geschrieben.

Somit lässt sich abschließend feststellen: . Die additive Gruppe ist also zyklisch und wird von der „1“ erzeugt.

Jetzt haben wir die Frage geklärt, ob die Gruppe von nur einem Element erzeugt werden kann. Es stellt sich jedoch erneut eine Frage. Unser Interesse gilt allen Zahlen, die auch die Gruppe erzeugen könnten. Wir suchen also andere Elemente , die auch die Gruppe erzeugen.

, z.B. , d.h. wir können feststellen, dass auch das Inverse des „Erzeugers“ erzeugt die ganze Gruppe.

Wir machen uns Gedanken darüber, nach welcher Methode wir unsere Frage beantworten können, und überlegen uns zwei verschiedene Strategien. Der erste Vorschlag ist das ganze theoretisch aufzubauen, die zweite Idee ist, es erst einmal mit Beispielen zu versuchen.

Der zweite Vorschlag wird dann auch in die Tat umgesetzt:

Beispiel n = 10,

Um der Frage nach den Erzeugern in diesem System nachzugehen, schließt sich an die Frontaldiskussion eine Arbeitsphase an, in der die Elemente der angegebenen Beispielmenge auf ihre Erzeugerfähigkeit überprüft werden.

Ergebnis dieser Arbeit:

Erzeuger:

Nicht-Erzeuger: .

Nach dieser Feststellung bleibt die Überlegung für eine allgemeine Formulierung.

Allgemeine Formulierung: ist ein Erzeuger der zyklischen Gruppe genau dann, wenn ggT(y, n) = 1 ist.

Anschließend soll diese allgemeine Formulierung bewiesen werden, ebenfalls wieder in Gruppenarbeit.

Beweis:

„<=“ XEA ergibt, dass , wobei a, b ganze Zahlen sind;

, daraus folgt

,

somit wissen wir, dass wir die mittels erzeugen können. Da aber eben schon herausgefunden wurde, dass Erzeuger der Gruppe ist, folgt die Behauptung, dass Erzeuger ist.

„=>“ Dieser Beweis geht quasi rückwärts, da y und n teilerfremd sind.

Bisher haben wir die additiv geschriebene zyklische Gruppe betrachtet. Ab jetzt wollen wir auch die multiplikative Gruppe betrachten.

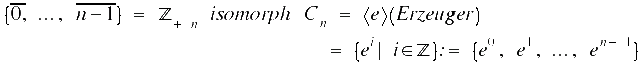
In der additiven Schreibweise war 0 das neutrale Element, jetzt ist diese Aufgabe der 1 zugeordnet. (Vielfache von n).

Es gibt also einen Übergang von der additiven zur multiplikativen Schreibweise:

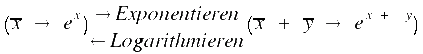
Es handelt sich also bei der multiplikativen und der additiven Gruppe um isomorphe Gruppen bzgl. zweier zueinander inverser Isomorphismen.

Dies beantwortet auch die Frage, wie die weiteren Erzeuger der (multiplikativ geschriebenen) zyklischen Gruppe aussehen: (analog zur Addition).

Wir betrachten nun die multiplikative Struktur von : Multiplikation, 1

4. Frage: Typ?

Bei dieser Menge handelt es sich um einen Monoid.

5. Frage: Welche Elemente sind invertierbar im Monoid?
, also die Menge aller „Töpfe“ die durch zu n teilerfremde Elemente repräsentiert werden.

Denn:

6. Frage: Was für eine Struktur hat ?

--> abgeschlossen unter Multiplikation:

Produkt ist auch invertierbar

--> Eins invertierbar => Monoid

--> jedes Element ist invertierbar => Gruppe

7. Frage: Wieviele Elemente hat diese Menge?

8. Frage: Wir haben noch keine explizite Formel. Wie sieht also die/eine Formel für diese Euler-Funktion aus?

Um diese Frage zu beantworten, wurde etwas diskutiert und im Anschluss daran wieder ein Beispiel vorgeschlagen. Als Ergebnis dieser Arbeitsphase wurde folgende Tabelle an der Tafel festgehalten:

Überlegungen zur Findung der Formel:

--> funktioniert, aber

funktioniert nicht!

--> Wenn n eine Primzahl ist, so ist , p: Primzahl

--> Chinesischer Restesatz:

Sie sind isomorph bezüglich Ring-mit-1.

Als Gruppe unter demselben Isomorphismus.

Vermutung:

Beweis:

„=>“: Es sei (x, y) Einheit.

Dann existieren (x', y') mit (x, y)(x', y') = (1, 1).

(x, y)(x', y') = (xx', yy').

„<=“: Es seien x, y Einheiten.

Dann existieren x' und y' mit xx' = 1, yy' = 1.

Es folgt: (x, y)(x', y') = (1, 1)

Jetzt haben wir unsere Vermutung bewiesen, es fehlt aber immer noch eine exakte Formel für die Eulersche Phi-Funktion.

Ist die Primzahlzerlegung von n in die verschiedenen Primzahlen , so ist .

Jetzt ist noch die Frage offen, wie man für Primzahl p und .

.

.

Es gibt demnach Elemente.

Es bleibt die Frage zu klären, welche Elemente x Vielfache von p sind und wieviele ich von diesen Elementen habe.

Um diese Frage zu beantworten, haben wir uns einen Zahlenstrahl vorgestellt, der mit dem „Nulltopf“ beginnt und den „p-Topf“ und seine Vielfachen aufweist.

Dabei kann man folgendes Beobachten:

.

Demnach gibt es Elemente, die durch p teilbar sind (= „Schlechten“).

Uns interessiert aber die Zahl der „Guten“, welche sich bestimmt zu .

Mit diesem Ergebnis können wir unsere Formel für die Euler Phi-Funktion vervollständigen und halten folgendes fest:

.

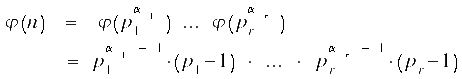Jetzt können wir abschließend an unserem obigen Beispiel überprüfen, ob und wie unsere Formel funktioniert:

n = 9: n = 3², p = 3, alpha = 2

j(9) = 3(3-1) = 6

Ein Vergleich dieses Ergebnisses mit dem aus unserer Tabelle zeigt eine Übereinstimmung.

n = 4: n= 2², p = 2, alpha = 2

j(4) = 2(2-1) = 2

Ein Vergleich mit der Tabelle liefert auch hier eine Übereinstimmung.

Somit haben wir eine Formel für die Eulersche Phi-Funktion gefunden, mit der auch die Einheitengruppe beschrieben werden kann.