


Next: About this document ...
1. Nachtrag zur †bungsstunde vom 31. 01. 2001.
Der fehlende Beweis aus der Übungsstunde wird zuerst
durchgeführt.
Beweis:
Per Konstruktion des Punktes 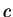 erhalten wir die Parallelogramme
erhalten wir die Parallelogramme
![$ \left[\begin{array}{cc}
a' & X \\ 0 & b
\end{array} \right]$](img3.gif) und
und
![$ \left[\begin{array}{cc}
a' & X \\ a & c
\end{array} \right]$](img4.gif) und analog per Konstruktion von
und analog per Konstruktion von 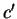 die Parallelogramme
die Parallelogramme
![$ \left[\begin{array}{cc}
b' & Y \\ 0 & a
\end{array} \right]$](img6.gif) und
und
![$ \left[\begin{array}{cc}
c' & Y \\ a' & a
\end{array} \right]$](img7.gif) . Also
ist
. Also
ist
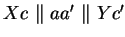 .
.
Zu zeigen ist, dass
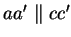 gilt. Dafür genügt es,
gilt. Dafür genügt es,
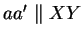 zu zeigen.
zu zeigen.
Ideen zur Problemlösung:
- (D) benutzen
- Überflüssiges weglassen
- Fehlendes einzeichnen
- Namen geben
- Symmetrien beachten
Hilfssatz: Es sei 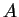 ein affiner Raum mit (D). Gegeben sei
ein Parallelogramm
ein affiner Raum mit (D). Gegeben sei
ein Parallelogramm
![$ \left[\begin{array}{cc}
b' & C \\ 0 & b
\end{array} \right]$](img13.gif) und ein Punkt
und ein Punkt 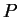 .
.
Bilde nun ein neues Parallelogramm
![$ \left[\begin{array}{cc}
a' & P \\ 0 & a
\end{array} \right]$](img15.gif) mit
mit
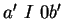 und
und 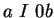 .
Definiere
.
Definiere 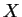 durch
durch
![$ \left[\begin{array}{cc}
a' & X \\ 0 & b
\end{array} \right]$](img3.gif) und
und 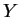 durch
durch
![$ \left[\begin{array}{cc}
b' & Y \\ 0 & a
\end{array} \right]$](img6.gif) .
(
.
(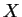 ist somit als vierter Parallelogrammpunkt eindeutig festgelegt.)
ist somit als vierter Parallelogrammpunkt eindeutig festgelegt.)
Betrachte
![$ \left[\begin{array}{cc}
b' & C \\ 0 & b
\end{array} \right]$](img13.gif) als festesParallelogramm. (Mit
als festesParallelogramm. (Mit 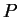 variieren auch die Punkte
variieren auch die Punkte
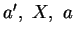 und
und 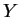 .)
.)
(Umformulierung des Problems: Bei welcher Lage von 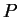 ist
ist
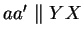 ?)
?)
Dann sind äquivalent:
-
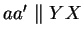
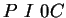
-
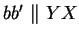 .
.
Beweis:
 Mit (D) gilt dann: Für das Zentrum
Mit (D) gilt dann: Für das Zentrum 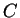 ist
ist
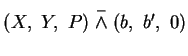 , also
, also
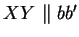 .
.
 :
:
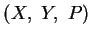 und
und
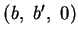 sind axiale Dreiecke. Somit gilt
sind axiale Dreiecke. Somit gilt 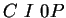 und
und 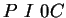 .
.
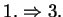 :
:
Da
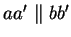 ist, folgt die Behauptung sofort.
ist, folgt die Behauptung sofort.
Somit ist der Hilfssatz bewiesen und wir können mit seiner Hilfe den
Beweis des Satzes beenden.
Nach Voraussetzung ist
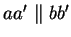 , also gilt nach dem Hilfssatz
(mit Zentrum 0 und unter Ausnutzung der Symmetrie)
, also gilt nach dem Hilfssatz
(mit Zentrum 0 und unter Ausnutzung der Symmetrie) 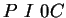 .
Ebenfalls nach dem Hilfssatz ist
.
Ebenfalls nach dem Hilfssatz ist
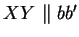 und somit ist
und somit ist
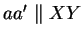 .
.
2. Fortsetzung des Vorlesungsstoffes
Zunächst werden aus der letzten Vorlesung die beiden Hilfssätze
noch einmal an der Tafel formuliert.
Hilfssatz 1: Gegeben sei eine affine Ebene mit (F), (D) und
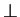 .
. 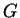 und
und 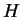 seien die Lotfußpunkte von
seien die Lotfußpunkte von 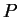 auf
auf 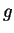 bzw.
bzw.
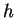 . Die Geraden
. Die Geraden 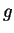 und
und 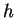 seien nicht isotrop. Dann sind
äquivalent:
seien nicht isotrop. Dann sind
äquivalent:
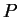 liegt auf einer Halbierenden.
liegt auf einer Halbierenden.
-
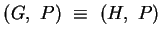 .
.
-
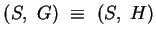 .
.
Hilfssatz 2: Ist 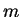 eine Halbierende, so ist auch das Lot
eine Halbierende, so ist auch das Lot
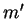 in
in  eine Halbierende.
eine Halbierende.
Der Beweis des zweiten Hilfssatzes war schon erarbeitet worden,
ebenso wie der Beweis der Inklusion
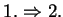 des
Hilfssatzes 1.
des
Hilfssatzes 1.
Beweis von Hilfssatz 1:
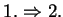 :
: 
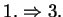 :
:
Bei einer Spiegelung bleibt Orthogonalität erhalten, wie auch die
Lotfußpunkte. Daraus folgt sofort die Behauptung.
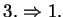 :
:
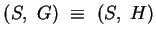 , d. h.
, d. h.
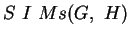 .
Die Frage ist nun, ob die Mittelsenkrechte von
.
Die Frage ist nun, ob die Mittelsenkrechte von 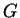 und
und 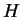 durch den Punkt
durch den Punkt
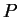 geht, welcher als Schnittpunkt der beiden Lote definiert ist.
geht, welcher als Schnittpunkt der beiden Lote definiert ist.
Die Spiegelung an der Mittelsenkrechte überführt den Punkt 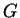 in
den Punkt
in
den Punkt 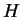 und umgekehrt, d. h. die Lote werden vertauscht. Der
Schnittpunkt der Lote aber bleibt derselbe, also ist
und umgekehrt, d. h. die Lote werden vertauscht. Der
Schnittpunkt der Lote aber bleibt derselbe, also ist 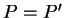 und
und
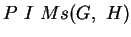 .
.
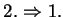 :
:
Der Beweis dieser Inklusion verläuft wegen der
Symmetrie analog
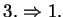 nur mit vertauschten Rollen von
nur mit vertauschten Rollen von
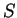 und
und 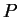 .
.



Next: About this document ...
Ellen Schramm
2001-02-11
![\includegraphics [height=8cm]{1_Bild1.epsf}](img1.gif)
![\includegraphics [height=8cm]{1_Bild1.epsf}](img1.gif)
![$ \left[\begin{array}{cc}
a' & X \\ 0 & b
\end{array} \right]$](img3.gif) und
und
![$ \left[\begin{array}{cc}
a' & X \\ a & c
\end{array} \right]$](img4.gif) und analog per Konstruktion von
und analog per Konstruktion von ![$ \left[\begin{array}{cc}
b' & Y \\ 0 & a
\end{array} \right]$](img6.gif) und
und
![$ \left[\begin{array}{cc}
c' & Y \\ a' & a
\end{array} \right]$](img7.gif) . Also
ist
. Also
ist
![\includegraphics [height=8cm]{1_Bild2.epsf}](img11.gif)
![$ \left[\begin{array}{cc}
b' & C \\ 0 & b
\end{array} \right]$](img13.gif) und ein Punkt
und ein Punkt ![$ \left[\begin{array}{cc}
a' & P \\ 0 & a
\end{array} \right]$](img15.gif) mit
mit
![$ \left[\begin{array}{cc}
a' & X \\ 0 & b
\end{array} \right]$](img3.gif) und
und ![$ \left[\begin{array}{cc}
b' & Y \\ 0 & a
\end{array} \right]$](img6.gif) .
(
.
(![$ \left[\begin{array}{cc}
b' & C \\ 0 & b
\end{array} \right]$](img13.gif) als festesParallelogramm. (Mit
als festesParallelogramm. (Mit 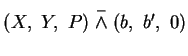 , also
, also
![\includegraphics [height=4cm]{1_Bild4.epsf}](img46.gif)
![\includegraphics [height=4cm]{1_Bild5.epsf}](img49.gif)