


Next: About this document ...
Ausgangspunkt der Überlegungen ist die Frage: Wie kann ein Zweieck
in 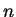 gleichmäßige Teile unterteilt werden?
gleichmäßige Teile unterteilt werden?
Definition: Gegeben sei ein affiner Raum mit (F) und (D).
Eine gleichmäßige Unterteilung eines Zweiecks 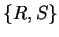 in
in
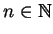 Teile ist eine Folge
Teile ist eine Folge
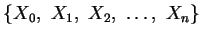 von Punkten, so dass
von Punkten, so dass 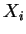 der Mittelpunkt von
der Mittelpunkt von
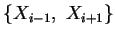 ist für
ist für
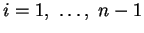 .
.
Warnung! Es ist möglich, dass nicht alle 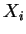 verschieden sind!
Beispiele:
verschieden sind!
Beispiele: 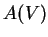 über Körpern endlicher Charakteristik.
über Körpern endlicher Charakteristik.
Satz: Gegeben sei ein Dreieck
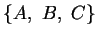 mit
Schwerpunkt (d. h. die Seitenhalbierenden sind nicht parallel). Es
sei
mit
Schwerpunkt (d. h. die Seitenhalbierenden sind nicht parallel). Es
sei
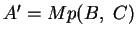 ,
,
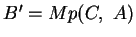 und
und
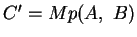 .
.
Dann hat das Zweieck
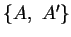 eine gleichmäßige Unterteilung in drei Teile, in der der
Schwerpunkt vorkommt.
eine gleichmäßige Unterteilung in drei Teile, in der der
Schwerpunkt vorkommt.
Beweis:
Dazu betrachtet man die Parallelprojektion 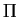 von
von 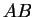 auf
auf 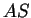 in Richtung
in Richtung 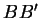 . Dabei geht der Mittelpunkt
. Dabei geht der Mittelpunkt 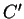 von
von 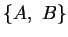 auf den Mittelpunkt
auf den Mittelpunkt 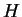 von
von 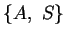 (vgl. Satz 3 der letzten Vorlesung). Zu zeigen ist, dass
(vgl. Satz 3 der letzten Vorlesung). Zu zeigen ist, dass
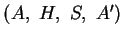 eine gleichmäßige Unterteilung von
eine gleichmäßige Unterteilung von
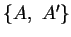 in drei
Teile ist.
in drei
Teile ist.
Nach Konstruktion ist 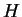 der Mittelpunkt von
der Mittelpunkt von 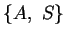 , also muss
noch gezeigt werden, dass
, also muss
noch gezeigt werden, dass 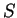 der Mittelpunkt von
der Mittelpunkt von
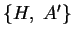 ist.
ist.
Zunächst gilt, dass
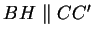 ist, da
ist, da
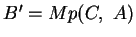 und
und
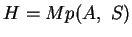 unter Parallelprojektion
in Richtung
unter Parallelprojektion
in Richtung 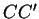 erhalten bleiben. Nun setzen wir
erhalten bleiben. Nun setzen wir
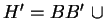 Parallele zu
Parallele zu 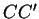 durch
durch 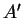 . Dann ist
. Dann ist
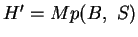 und analog
und analog
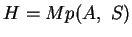 .
.
Betrachten wir nun das Tetragon
![$ \left [ B'\ A' \atop H \ H' \right],$](img33.gif) so ist
so ist
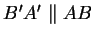 als Mittenlinie des Mittendreiecks
als Mittenlinie des Mittendreiecks
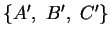 (vgl. Satz aus letzter Vorlesung). Ebenso ist
(vgl. Satz aus letzter Vorlesung). Ebenso ist
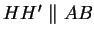 als Mittenlinie des Mittendreiecks
als Mittenlinie des Mittendreiecks
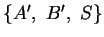 .
.
Also ist das Tetragon ein Parallelogramm, dessen Diagonalen sich im
Punkt 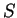 schneiden. Somit ist
schneiden. Somit ist 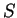 der Mittelpunkt der
Diagonalzweiecke, also insbesondere der Mittelpunkt von
der Mittelpunkt der
Diagonalzweiecke, also insbesondere der Mittelpunkt von
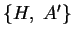 .
Der Beweis des Satzes hat uns ein weiteres Ergebnis geliefert: Das
Zweieck
.
Der Beweis des Satzes hat uns ein weiteres Ergebnis geliefert: Das
Zweieck 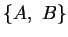 hat die gleichmäßige Unterteilung
hat die gleichmäßige Unterteilung
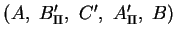 in vier Teile, denn:
in vier Teile, denn:
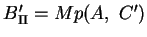 , da
, da
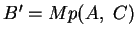 unter
unter 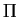 auf
auf
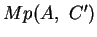 abgebildet wird. Analoges gilt für
abgebildet wird. Analoges gilt für
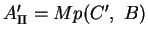 .
.
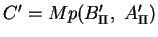 , da
, da
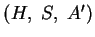 unter
unter 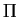 auf
auf
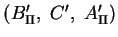 abgebildet wird und
abgebildet wird und 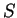 nach dem
vorher bewiesenen Satz der Mittelpunkt von
nach dem
vorher bewiesenen Satz der Mittelpunkt von
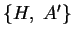 ist.
ist.
Wir wollen nun eine gleichmäßige Unterteilung von 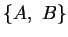 in
in 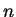 Teile konstruieren.
Teile konstruieren.
1. Fall: Wir betrachten eine Unterteilung in 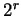 Teile. Eine solche
Unterteilung ist durch iterative Mittelpunktsbildung immer möglich.
Allerdings bleibt die Frage, ob es sich dabei um eine
gleichmäßige Unterteilung handelt, zu beantworten.
Teile. Eine solche
Unterteilung ist durch iterative Mittelpunktsbildung immer möglich.
Allerdings bleibt die Frage, ob es sich dabei um eine
gleichmäßige Unterteilung handelt, zu beantworten.
Zunächst betrachten wir 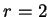 :
Ist
:
Ist
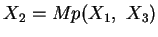 ? Die Unterteilung eines Zweiecks in
vier gleiche Teile haben wir für Dreiecke gezeigt (weiteres
Ergebnis). Ein dritter Punkt
? Die Unterteilung eines Zweiecks in
vier gleiche Teile haben wir für Dreiecke gezeigt (weiteres
Ergebnis). Ein dritter Punkt 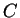 , welcher mit
, welcher mit 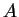 und
und 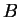 ein Dreieck bildet, liefert also die Behauptung.
ein Dreieck bildet, liefert also die Behauptung.
Das bedeutet, dass wir mindestens eine affine Ebene mit (F), (D) und
(S) brauchen, eine affine Gerade reicht nicht aus,
da dort kein Dreieck existiert!
Für 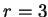 wird der Fall
wird der Fall 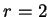 außen für
außen für
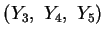 angewendet. Vollständige Induktion liefert dann die Behauptung.
angewendet. Vollständige Induktion liefert dann die Behauptung.
2. Fall: Es sei 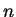 keine Zweierpotenz.
keine Zweierpotenz.
Wir wählen nun
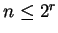 und einen Punkt
und einen Punkt
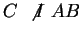 .
. 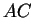 wird in
wird in 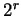 Teile
Teile
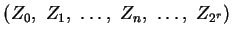 unterteilt und der Punkt
unterteilt und der Punkt 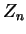 mit dem Punkt
mit dem Punkt 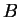 verbunden.
Eine Parallelprojektion (von der wir noch nicht wissen, ob sie
überhaupt existiert !) in Richtung
verbunden.
Eine Parallelprojektion (von der wir noch nicht wissen, ob sie
überhaupt existiert !) in Richtung 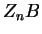 auf
auf 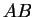 liefert eine
gleichmäßige Unterteilung von
liefert eine
gleichmäßige Unterteilung von 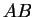 in
in 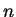 Teile.
Teile.
Bleibt noch das Problem der Existenz der Parallelprojektion. Diese
existiert, falls
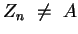 gilt. Um diesem Problem aus dem
Weg zu gehen, fordern wir schon in der Voraussetzung, dass alle Punkte
voneinander verschieden sind.
gilt. Um diesem Problem aus dem
Weg zu gehen, fordern wir schon in der Voraussetzung, dass alle Punkte
voneinander verschieden sind.
Definition: Gegeben sei ein affiner Raum mit (F), (D) und
(S). Eine Skala auf der Geraden g mit geordnetem
Einheitszweieck 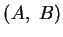 [für
[für
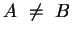 auf
auf 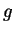 ] ist eine
Folge
] ist eine
Folge
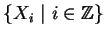 von Punkten auf
von Punkten auf 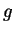 mit der
Eigenschaft
mit der
Eigenschaft
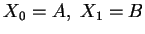 und
und
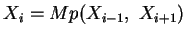 .
.



Next: About this document ...
Ellen Schramm
2001-01-28
![\includegraphics [height=4cm]{18_Bild1a.epsf}](img14.gif)
![\includegraphics [height=4cm]{18_Bild1a.epsf}](img14.gif)
![\includegraphics [height=6cm]{18_Bild2a.epsf}](img32.gif)
![$ \left [ B'\ A' \atop H \ H' \right],$](img33.gif) so ist
so ist
![\includegraphics [height=2cm]{18_Bild3a.epsf}](img48.gif)
![\includegraphics [height=3cm]{18_Bild4a.epsf}](img54.gif)
![\includegraphics [height=2cm]{18_Bild5a.epsf}](img57.gif)
![\includegraphics [height=6cm]{18_Bild6a.epsf}](img64.gif)