Date: February 19th, 2004
This chapter has three aims. First it shows how the GAP system [GAP24] can be utilized to construct character tables of certain central extensions from known character tables; the GAP functions used for that are part of the GAP Character Table Library [Bre25]. Second it documents several constructions of character tables which are contained in the GAP Character Table Library. Third it serves as a testfile for the GAP functions.
A typo (wrong sign of \(\varepsilon^5\)) in the picture in Section 3.1-4 has been corrected in 2013.
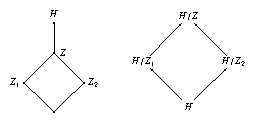
In this section, we will deal with the following situation. Let \(H\) be a group, \(Z\) be a cyclic central subgroup in \(H\), and \(Z = Z_1 Z_2\) for subgroups \(Z_1\) and \(Z_2\) of coprime orders \(m\) and \(n\), say. For the sake of simplicity, suppose that both \(m\) and \(n\) are primes; the general case is then obtained by iterating the construction process.
Our aim is to compute the character table of \(H\) from the character tables of \(H/Z_1\) and \(H/Z_2\). We assume that the factor fusions from these tables to that of the common factor group \(H/Z\) are known. Again for the sake of simplicity, we will take the character table of \(H/Z\) as an input. (See Section 3.2-4 for an example where two different orderings of classes and characters of \(H/Z\) arise from the tables of \(H/Z_1\) and \(H/Z_2\).)
For example, the character table of \(H = 12.M_{22}\) can be computed from those of \(6.M_{22}\) and \(4.M_{22}\), and the character table of \(6.M_{22}\) can be computed from those of \(3.M_{22}\) and \(2.M_{22}\) (see Section 3.2-1).
The conjugacy classes and power maps of \(H\) are uniquely determined by the input data specified above.

Suppose that a class \(C\) of elements of \(H/Z\) has \(n_C\) preimage classes in \(H/Z_1\) and \(m_C\) preimage classes in \(H/Z_2\); then \(n_C\) is either \(1\) or \(n\), and \(m_C\) is either \(1\) or \(m\). The preimage classes of \(C\) in \(H/Z_1\) and \(H/Z_2\) are parametrized by \(\{ j; 0 \leq j < n_C \}\) and \(\{ i; 0 \leq i < m_C \}\), respectively, and the preimage classes in \(H\) are parametrized by the pairs \(\{ (i,j); 0 \leq i < m_C, 0 \leq j < n_C \}\).
The centralizer orders of these classes in \(H\) are \(m_C n_C\) times the centralizer order of \(C\) in \(H/Z\).
The factor fusion onto \(H/Z_1\) is then given by mapping the class with the parameter \((i,j)\) to the class with the parameter \(j\); analogously, the factor fusion onto \(H/Z_2\) maps this class to the class with the parameter \(i\). To see this, let \(Z = \langle z \rangle\), and set \(z_1 = z^n\) and \(z_2 = z^m\). Now take an element \(g \in H\) for which \(g Z\) lies in \(C\). Then the elements \(g z_1^i z_2^j\), \(1 \leq i \leq m_C\), \(1 \leq j \leq n_C\) form a set of representatives of the preimage classes of \(C\) in \(H\). In \(H/Z_1\) and \(H/Z_2\), these elements map to \(g z_2^j Z_1\), \(1 \leq j \leq n_C\) and \(g z_1^i Z_2\), \(1 \leq i \leq m_C\), respectively, which are sets of representatives of the classes in question in these groups.
For each prime \(p\), the factor fusions determine the \(p\)-th power map of \(H\) from the \(p\)-th power maps of \(H/Z_1\) and \(H/Z_2\). To see this, take a class \(C_0\) in \(H\) that is a preimage of the class \(C\) of \(H/Z\), and let \(K\) be the class of \(p\)-th powers of the elements in \(C\). Then the image of \(C_0\) under the \(p\)-th power map is one of the preimages of \(K\). We know the images of \(C_0\) under the factor fusions to \(H/Z_1\) and \(H/Z_2\), and thus also their images \(K_1\) and \(K_2\) under the \(p\)-th power maps of these groups. So the class of \(p\)-th powers of the elements in \(C_0\) is the unique class that is mapped to \(K_1\) and \(K_2\) under the factor fusions.
The construction of the character table head of \(H\) from the input data specified above is implemented by the GAP function CharacterTableOfCommonCentralExtension (CTblLib: CharacterTableOfCommonCentralExtension).
First of all, it should be said that it is not obvious how the irreducible characters of \(H\) can be computed from the irreducible characters of \(H/Z_1\) and \(H/Z_2\). Clearly the irreducible characters of the two factor groups can be inflated to \(H\) via the factor fusions, so we have to find those irreducibles that have neither \(Z_1\) nor \(Z_2\) in their kernels.
For that, we use the following heuristic. Let \(\varepsilon_z\) be a complex primitive \(|z|\)-th root of unity. For integers \(i\), set \(Irr_{{z,i}}(H) = \{ \chi \in Irr(H); \chi(z) = \varepsilon_z^i \chi(1) \}\). Then \(Irr(H) = \bigcup_{{i=0}}^{{|z|-1}} Irr_{{z,i}}(H)\), as a disjoint union. If \(i\) is a multiple of \(m\) or \(n\), respectively, then \(Irr_{{z,i}}(H)\) consists of the inflations of certain irreducible characters of \(H/Z_1\) or \(H/Z_2\), respectively. The remaining irreducible characters of \(H\) lie in \(Irr_{{z,i}}(H)\) with \(i\) coprime to \(|z|\). These characters are algebraic conjugates of \(Irr_{{z,1}}(H)\), so it suffices to compute this subset; the conjugates are then derived as the last step.
Since \(Irr_{{z,i}}(H) \otimes Irr_{{z,j}}(H) \subset ℤ[ Irr_{{z,i+j}}(H) ]\) holds, we start with the tensor products of the known irreducible characters in \(Irr_{{z,i}}(H)\) and \(Irr_{{z,j}}(H)\) with the property \(i+j \equiv 1 \bmod m n\).
For example, if we have \(m = 2\) and \(n = 3\) then \(Irr_{{z,3}}(H)\) consists of the inflations of those characters in \(Irr(H/Z_2)\) that are not characters of \(H/Z\), and \(Irr_{{z,4}}(H)\) consists of the inflations of certain characters in \(Irr(H/Z_1)\) that are not characters of \(H/Z\). The tensor products of these sets of characters lie in the span of \(Irr_{{z,1}}(H)\).
In general these tensor products are reducible, but some of them may be in fact irreducible, so we first take these irreducibles, and reduce the other tensor products with them. (If \(H\) is a direct product of \(Z\) and \(H/Z\) then all missing irreducibles are obtained this way.)
Then we tensor algebraic conjugates of the known characters in the span of \(Irr_{{z,1}}(H)\) with characters in suitable sets \(Irr_{{z,i}}(H)\), in order to get more characters in \(Irr_{{z,1}}(H)\); for example, \(Irr_{{z,1}}(H) \otimes Irr_{{z,0}}(H)\) is a subset of \(ℤ[Irr_{{z,1}}(H)]\).
In the case \(m = 2\) and \(n = 3\), also \(Irr_{{z,5}}(H) \otimes Irr_{{z,2}}(H)\) yields linear combinations of \(Irr_{{z,1}}(H)\). Note that \(Irr_{{z,5}}(H)\) consists of the complex conjugates of \(Irr_{{z,1}}(H)\).
In the next step, we apply the LLL algorithm (implemented via the GAP function LLL (Reference: LLL)) to the set of reducible characters in \(ℤ[Irr_{{z,1}}(H)]\) which we got from the tensor products, and hope to find irreducibles. In the examples shown below, this step yields all desired irreducible characters.
The GAP function CharacterTableOfCommonCentralExtension (CTblLib: CharacterTableOfCommonCentralExtension) implements the strategy sketched above.
One natural
choice for the ordering of the columns in the character table of \(H\) is given by respecting the ordering of columns in the character table of \(H/Z\), and taking the preimage of the class \(C\) corresponding to the parameter \((k \bmod m_C, k \bmod n_C)\) as the \(k\)-th class for \(C\).
If the preimages of \(C\) in \(H/Z_1\) and \(H/Z_2\) have class representatives \(g Z_1\), \(g z_2 Z_1\), \(g z_2^2 Z_1\), \(\ldots\) and \(g Z_2\), \(g z_1 Z_2\), \(g z_1^2 Z_2\), \(\ldots\), respectively (in this ordering), then the above rule yields representatives of preimages in \(H\) in the ordering \(g\), \(g (z_1 z_2)\), \(g (z_1 z_2)^2\), \(\ldots\).
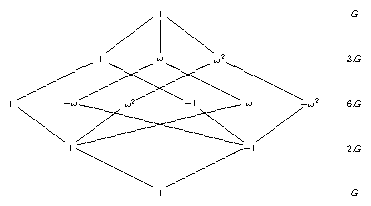
In the case \(m = 2\), \(n = 3\), the following pattern arises for classes of \(H/Z\) that have \(m\) and \(n\) preimages in \(H/Z_1\) and \(H/Z_2\), respectively. The vertices are labelled by the roots of unity with which the values of the characters in the set \(Irr_{{z,1}}(H)\) on the first preimage must be multiplied in order to obtain the values on the given class; we have \(\omega = \exp(2 \pi i/3)\).
It may happen that a cyclic central subgroup \(Z_0\) of \(H\) contains \(Z\) properly. Then we choose a class ordering relative to that in the factor group \(H/Z_0\), mainly because the Atlas tables of this type are sorted this way.
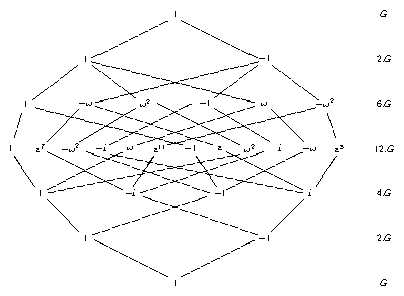
The typical case is the character table of a central extension of the type \(12.G\) that shall be constructed from the character tables of the groups of the types \(4.G\) and \(6.G\); here we prefer to order the preimages of a class in the smaller factor group of the type \(G\) according to the above rule. This results in the following pattern, where \(\varepsilon = \exp(2 \pi i/12)\) holds (cf. Section ATLAS Tables
in the manual of the GAP Character Table Library).
A more important aspect concerns the computation of the irreducible characters. Let \(Z_0 = \langle z_0 \rangle\). Instead of computing \(Irr_{{z,1}}(H)\), we compute the set \(Irr_{{z_0,1}}(H)\).
In the computation of the character table of a central extension of the type \(12.G\) as mentioned above, with \(|z_0| = 12\), we start with the characters
\[ Irr_{{z_0,3}}(H) \otimes Irr_{{z_0,10}}(H) \cup Irr_{{z_0,4}}(H) \otimes Irr_{{z_0,9}}(H) \subseteq ℤ[Irr_{{z_0,1}}(H)], \]
and later form tensor products involving algebraic conjugates of the characters in the span of \(Irr_{{z_0,1}}(H)\), using that
\[ Irr_{{z_0,1}}(H) \otimes Irr_{{z_0,0}}(H) \cup Irr_{{z_0,2}}(H) \otimes Irr_{{z_0,11}}(H) \cup Irr_{{z_0,5}}(H) \otimes Irr_{{z_0,8}}(H) \cup Irr_{{z_0,6}}(H) \otimes Irr_{{z_0,7}}(H) \]
is a subset of \(ℤ[Irr_{{z_0,1}}(H)]\).
Without that modification, the computation of irreducibles is significantly more involved.
The GAP function CharacterTableOfCommonCentralExtension (CTblLib: CharacterTableOfCommonCentralExtension) chooses the class ordering relative to larger cyclic factor groups, as in the above picture, and also uses the above refinement for the computation of irreducible characters.
The following examples use the GAP Character Table Library, so we first load this package.
gap> LoadPackage( "ctbllib", false ); true
For the following groups, the Atlas contains the character tables of central extensions \(M.G\) of simple groups \(G\) with \(|M|\) divisible by two different primes; in all these cases, we have \(M \in \{ 6, 12 \}\).
(The entry concerning \(6.{}^2E_6(2)\) has been added to the list after the character table of \(3.{}^2E_6(2)\) became available. This table has been computed by Frank Lübeck.)
gap> list:= [ > # G m.G n.G mn.G > > [ "A6", "2.A6", "3.A6", "6.A6" ], > [ "A7", "2.A7", "3.A7", "6.A7" ], > [ "L3(4)", "2.L3(4)", "3.L3(4)", "6.L3(4)" ], > [ "2.L3(4)", "4_1.L3(4)", "6.L3(4)", "12_1.L3(4)" ], > [ "2.L3(4)", "4_2.L3(4)", "6.L3(4)", "12_2.L3(4)" ], > [ "M22", "2.M22", "3.M22", "6.M22" ], > [ "2.M22", "4.M22", "6.M22", "12.M22" ], > [ "U4(3)", "2.U4(3)", "3_1.U4(3)", "6_1.U4(3)" ], > [ "U4(3)", "2.U4(3)", "3_2.U4(3)", "6_2.U4(3)" ], > [ "2.U4(3)", "4.U4(3)", "6_1.U4(3)", "12_1.U4(3)" ], > [ "2.U4(3)", "4.U4(3)", "6_2.U4(3)", "12_2.U4(3)" ], > [ "O7(3)", "2.O7(3)", "3.O7(3)", "6.O7(3)" ], > [ "U6(2)", "2.U6(2)", "3.U6(2)", "6.U6(2)" ], > [ "Suz", "2.Suz", "3.Suz", "6.Suz" ], > [ "Fi22", "2.Fi22", "3.Fi22", "6.Fi22" ], > [ "2E6(2)", "2.2E6(2)", "3.2E6(2)", "6.2E6(2)" ], > ];;
As was discussed in the sections 3.1-3 and 3.1-4, the class ordering of the result tables is the same as that in the GAP library tables, so it is enough to check whether the set of characters in the computed table coincides with the set of characters in the library table.
In order to list information about the progress, we set the relevant info level to \(1\).
gap> SetInfoLevel( InfoCharacterTable, 1 ); gap> for entry in list do > id := entry[4]; > tblG := CharacterTable( entry[1] ); > tblmG := CharacterTable( entry[2] ); > tblnG := CharacterTable( entry[3] ); > lib := CharacterTable( id ); > res:= CharacterTableOfCommonCentralExtension( tblG, tblmG, tblnG, id ); > if not res.IsComplete then > Print( "#E not complete: ", id, "\n" ); > fi; > if not IsSubset( Irr( lib ), res.irreducibles ) then > Print( "#E inconsistent: ", id, "\n" ); > fi; > od; #I 6.A6: need 4 faithful irreducibles #I 6.A6: 4 found by tensoring #I 6.A7: need 5 faithful irreducibles #I 6.A7: 5 found by tensoring #I 6.L3(4): need 7 faithful irreducibles #I 6.L3(4): 7 found by LLL #I 12_1.L3(4): need 5 faithful irreducibles #I 12_1.L3(4): 2 found by tensoring #I 12_1.L3(4): 3 found by tensoring #I 12_2.L3(4): need 6 faithful irreducibles #I 12_2.L3(4): 6 found by LLL #I 6.M22: need 10 faithful irreducibles #I 6.M22: 1 found by tensoring #I 6.M22: 9 found by LLL #I 12.M22: need 7 faithful irreducibles #I 12.M22: 7 found by LLL #I 6_1.U4(3): need 15 faithful irreducibles #I 6_1.U4(3): 1 found by tensoring #I 6_1.U4(3): 14 found by LLL #I 6_2.U4(3): need 12 faithful irreducibles #I 6_2.U4(3): 12 found by LLL #I 12_1.U4(3): need 12 faithful irreducibles #I 12_1.U4(3): 4 found by tensoring #I 12_1.U4(3): 8 found by tensoring #I 12_2.U4(3): need 9 faithful irreducibles #I 12_2.U4(3): 9 found by LLL #I 6.O7(3): need 12 faithful irreducibles #I 6.O7(3): 2 found by tensoring #I 6.O7(3): 10 found by LLL #I 6.U6(2): need 28 faithful irreducibles #I 6.U6(2): 2 found by tensoring #I 6.U6(2): 26 found by LLL #I 6.Suz: need 29 faithful irreducibles #I 6.Suz: 29 found by LLL #I 6.Fi22: need 34 faithful irreducibles #I 6.Fi22: 4 found by tensoring #I 6.Fi22: 30 found by LLL #I 6.2E6(2): need 60 faithful irreducibles #I 6.2E6(2): 60 found by LLL gap> SetInfoLevel( InfoCharacterTable, 0 );
We see that in all cases, the irreducible characters of the groups \(M.G\) are obtained by reducing tensor products and applying the LLL algorithm.
The following cases also fit to the pattern introduced above.
(The following examples were added in October 2006.)
The group \((2^2 \times 3).L_3(4)\) can be viewed as a common central extension of its factor group \(2.L_3(4)\) by the two groups \(2^2.L_3(4)\) and \(6.L_3(4)\).
Analogously, the group \((4^2 \times 3).L_3(4)\) can be viewed as a common central extension of its factor group \((2 \times 4).L_3(4)\) by the two groups \(4^2.L_3(4)\) and \((2 \times 12).L_3(4)\).
Finally, the group \((2 \times 12).L_3(4)\) can be viewed as a common central extension of the factor group \(2^2.L_3(4)\) by the two groups \((2 \times 4).L_3(4)\) and \((2^2 \times 3).L_3(4)\).
The construction of the character tables of the involved factor groups \(2^2.L_3(4)\) and \((2 \times 4).L_3(4)\), as well as an alternative construction of the table of \((2 \times 12).L_3(4)\) can be found in the sections 2.7-2 and 2.7-4.
gap> list2:= [ > [ "2.L3(4)", "2^2.L3(4)", "6.L3(4)", "(2^2x3).L3(4)" ], > [ "2^2.L3(4)", "(2x4).L3(4)", "(2^2x3).L3(4)", "(2x12).L3(4)" ], > [ "(2x4).L3(4)", "4^2.L3(4)", "(2x12).L3(4)", "(4^2x3).L3(4)" ], > ];;
(The following examples were added in December 2010.)
The group \((3^2 \times 2).U_4(3)\) can be viewed as a common central extension of its factor group \(3_1.U_4(3)\) by the two groups \(6_1.U_4(3)\) and \(3^2.U_4(3)\), or as a common central extension of its factor group \(3_2.U_4(3)\) by the two groups \(6_2.U_4(3)\) and \(3^2.U_4(3)\).
Analogously, the group \((3^2 \times 4).U_4(3)\) can be viewed as a common central extension of its factor group \(6_1.U_4(3)\) by the two groups \(12_1.U_4(3)\) and \((3^2 \times 2).U_4(3)\), or as a common central extension of its factor group \(6_2.U_4(3)\) by the two groups \(12_2.U_4(3)\) and \((3^2 \times 2).U_4(3)\).
gap> Append( list2, [ > [ "3_1.U4(3)", "6_1.U4(3)", "3^2.U4(3)", "(3^2x2).U4(3)" ], > [ "3_2.U4(3)", "6_2.U4(3)", "3^2.U4(3)", "(3^2x2).U4(3)" ], > [ "6_1.U4(3)", "12_1.U4(3)", "(3^2x2).U4(3)", "(3^2x4).U4(3)" ], > [ "6_2.U4(3)", "12_2.U4(3)", "(3^2x2).U4(3)", "(3^2x4).U4(3)" ], > ] ); gap> SetInfoLevel( InfoCharacterTable, 1 ); gap> for entry in list2 do > id := entry[4]; > tblG := CharacterTable( entry[1] ); > tblmG := CharacterTable( entry[2] ); > tblnG := CharacterTable( entry[3] ); > lib := CharacterTable( id ); > res:= CharacterTableOfCommonCentralExtension( > tblG, tblmG, tblnG, id ); > if not res.IsComplete then > Print( "#E not complete: ", id, "\n" ); > fi; > if TransformingPermutationsCharacterTables( res.tblmnG, lib ) > = fail then > Print( "#E inconsistent: ", id, "\n" ); > fi; > od; #I (2^2x3).L3(4): need 14 faithful irreducibles #I (2^2x3).L3(4): 14 found by tensoring #I (2x12).L3(4): need 11 faithful irreducibles #I (2x12).L3(4): 7 found by tensoring #I (2x12).L3(4): 4 found by LLL #I (4^2x3).L3(4): need 22 faithful irreducibles #I (4^2x3).L3(4): 14 found by tensoring #I (4^2x3).L3(4): 8 found by LLL #I (3^2x2).U4(3): need 39 faithful irreducibles #I (3^2x2).U4(3): 27 found by tensoring #I (3^2x2).U4(3): 12 found by LLL #I (3^2x2).U4(3): need 42 faithful irreducibles #I (3^2x2).U4(3): 2 found by tensoring #I (3^2x2).U4(3): 40 found by LLL #I (3^2x4).U4(3): need 30 faithful irreducibles #I (3^2x4).U4(3): 6 found by tensoring #I (3^2x4).U4(3): 8 found by tensoring #I (3^2x4).U4(3): 16 found by LLL #I (3^2x4).U4(3): need 33 faithful irreducibles #I (3^2x4).U4(3): 9 found by tensoring #I (3^2x4).U4(3): 18 found by tensoring #I (3^2x4).U4(3): 6 found by further tensoring gap> SetInfoLevel( InfoCharacterTable, 0 );
The GAP Character Table Library contains the character tables of all maximal subgroups of the groups \(4.M_{22}\), \(3.M_{22}\), \(2.Suz\), and \(3.Suz\). So we can use the approach from Section 3.1 for computing the character tables of the maximal subgroups of \(6.M_{22}\), \(12.M_{22}\), and \(6.Suz\).
These tables are contained in the GAP Character Table Library. Several of the groups are direct products, and the library tables of direct products are usually stored in the form of Kronecker products of the tables of the factors, so the class ordering of the result tables does not necessarily coincide with the class ordering in the library tables.
gap> sublist:= list{ [ 6, 7, 14 ] }; [ [ "M22", "2.M22", "3.M22", "6.M22" ], [ "2.M22", "4.M22", "6.M22", "12.M22" ], [ "Suz", "2.Suz", "3.Suz", "6.Suz" ] ] gap> for entry in sublist do > tblG := CharacterTable( entry[1] ); > tblmG := CharacterTable( entry[2] ); > tblnG := CharacterTable( entry[3] ); > lib := CharacterTable( entry[4] ); > > maxesG := List( Maxes( tblG ), CharacterTable ); > maxesmG := List( Maxes( tblmG ), CharacterTable ); > maxesnG := List( Maxes( tblnG ), CharacterTable ); > maxeslib := List( Maxes( lib ), CharacterTable ); > > for i in [ 1 .. Length( maxesG ) ] do > id:= Identifier( maxeslib[i] ); > res:= CharacterTableOfCommonCentralExtension( maxesG[i], > maxesmG[i], maxesnG[i], id ); > if not res.IsComplete then > Print( "#E not complete: ", id, "\n" ); > fi; > if not IsSubset( Irr( maxeslib[i] ), res.irreducibles ) then > trans:= TransformingPermutationsCharacterTables( maxeslib[i], > res.tblmnG ); > if not IsRecord( trans ) then > Print( "#E not transformable: ", id, "\n" ); > fi; > fi; > od; > od;
Since we get no output, all tables in question can be computed with the GAP functions, and coincide (up to permutations of rows and columns) with the library tables.
2B Centralizer in \(3.Fi_{24}'\) (January 2004)As is stated in [CCN+85, p. 207], the 2B centralizer \(N_0\) in the sporadic simple Fischer group \(Fi_{24}'\) has the structure \(2^{{1+12}}_+.3U_4(3).2_2\). The character table of \(N_0\) is contained in the GAP Character Table Library since the year \(2000\).
Our aim is to compute the character table of the preimage \(N\) of \(N_0\) in the central extension \(3.Fi_{24}'\) of \(Fi_{24}'\); let \(Z_1\) denote the centre of \(3.Fi_{24}'\).
Using the dihedral group method
in the faithful permutation representation of degree \(920\,808\) for \(3.Fi_{24}'\), we first compute a generating set of \(N\). This group has three orbits of the lengths \(774\,144\), \(145\,152\), and \(1\,512\); the actions on the first two orbits are faithful, and the action on the orbit of length \(1\,512\) (which consists of the fixed points of the central involution of \(N\)) has kernel exactly the central subgroup \(Z_2\), say, of order \(2\) in \(N\).
Since the permutation representation on \(1\,512\) points is so small, it is straightforward to compute the character table of \(N/Z_2\) using the implementation of Dixon's algorithm in GAP; now this table is part of the GAP Character Table Library.
Note that \(N\) is a central extension of \(N_0/Z(N_0)\) by the cyclic group \(Z = Z_1 Z_2\) of order \(6\), and that we know the character tables of the groups \(N/Z_1\) and \(N/Z_2\). So we can apply the method described in Section 3.1 for computing the character table of \(N\).
First we fetch the input data.
gap> tblmG := CharacterTable( "F3+N2B" );; gap> tblG := tblmG / ClassPositionsOfCentre( tblmG );; gap> tblnG := CharacterTable( "2^12.3^2.U4(3).2_2'" );;
The character tables of the library table of \(N_0\) and the character table of \(N/Z_2\) obtained from the permutation group are not compatible in the sense that the tables of the factor groups modulo the centres are not sorted compatibly, so we have to compute and store the fusion from tblnG to tblG.
gap> f2:= tblnG / ClassPositionsOfCentre( tblnG );; gap> trans:= TransformingPermutationsCharacterTables( f2, tblG );; gap> tblnGfustblG:= OnTuples( GetFusionMap( tblnG, f2 ), > trans.columns );; gap> StoreFusion( tblnG, tblnGfustblG, tblG ); gap> IsSubset( Irr( tblnG ), > List( Irr( tblG ), x -> x{ tblnGfustblG } ) ); true
Now we apply CharacterTableOfCommonCentralExtension (CTblLib: CharacterTableOfCommonCentralExtension).
gap> SetInfoLevel( InfoCharacterTable, 1 ); gap> id:= "3.2^(1+12).3U4(3).2";; gap> res:= CharacterTableOfCommonCentralExtension( > tblG, tblmG, tblnG, id );; #I 3.2^(1+12).3U4(3).2: need 36 faithful irreducibles #I 3.2^(1+12).3U4(3).2: 16 found by tensoring #I 3.2^(1+12).3U4(3).2: 20 found by LLL gap> SetInfoLevel( InfoCharacterTable, 0 );
So we have found all missing irreducibles of \(N\). Let us check whether the result table coincides with the table in the GAP Character Table Library.
gap> lib:= CharacterTable( "3.F3+N2B" );; gap> IsRecord( TransformingPermutationsCharacterTables( > res.tblmnG, lib ) ); true
We were interested in the character table because \(N\) is a maximal subgroup of \(3.Fi_{24}'\). So the class fusion into the table of this group is an interesting information. We assume that the class fusion of \(N_0\) into \(Fi_{24}'\) is known, and compute only those possible class fusions that are compatible with this map.
gap> 3f3p:= CharacterTable( "3.F3+" );; gap> f3p:= CharacterTable( "F3+" );; gap> approxfus:= CompositionMaps( > InverseMap( GetFusionMap( 3f3p, f3p ) ), > CompositionMaps( GetFusionMap( tblmG, f3p ), > GetFusionMap( lib, tblmG ) ) );; gap> poss:= PossibleClassFusions( lib, 3f3p, > rec( fusionmap:= approxfus ) );; gap> Length( poss ); 1
It turns out that only one map has this property. (Without the condition on the compatibility, we would have got \(128\) possibilities, which form one orbit under table automorphisms.)
generated by GAPDoc2HTML