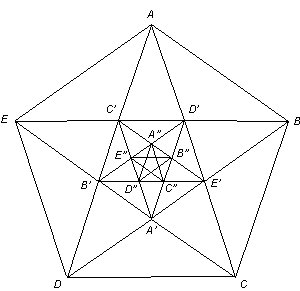
Das Pentagramm
Johann Wolfgang Goethe: "Faust", Der Tragödie erster Teil, Z. 1384 - Z.1408
(...)
MEPHISTOPHELES.
Wir wollen wirklich uns besinnen,
Die nächsten Male
mehr davon!
Dürft ich wohl diesmal mich entfernen?
FAUST.
Ich sehe nicht, warum du fragst.
Ich habe jetzt dich kennen
lernen
Besuche nun mich, wie du magst.
Hier ist das Fenster, hier die
Türe,
Ein Rauchfang ist dir auch gewiß.
MEPHISTOPHELES.
Gesteh ichs nur! daß ich hinausspaziere,
Verbietet
mir ein kleines Hindernis,
Der Drudenfuß auf Eurer Schwelle
FAUST.
Das Pentagramma macht dir Pein?
Ei sage mir, du Sohn der
Hölle,
Wenn das dich bannt, wie kamst du denn herein?
Wie ward ein
solcher Geist betrogen?
MEPHISTOPHELES.
Beschaut es recht! es ist nicht gut gezogen:
Der eine
Winkel, der nach außen zu,
Ist, wie du siehst, ein wenig offen.
FAUST.
Das hat der Zufall gut getroffen!
Und mein Gefangner wärst
denn du?
Das ist von ungefähr gelungen!
MEPHISTOPHELES.
Der Pudel merkte nichts, als er hereingesprungen,
Die
Sache sieht jetzt anders aus:
Der Teufel kann nicht aus dem Haus.
(...)
Doch schon lange vor Goethe war das Pentagramm ein besonderes Symbol:
Die Phythagoreer benutzten es ca. 500 v. Chr. als Geheimzeichen für ihren Bund. Die Pythagoreer glaubten, dass zwei gleichartige Größen immer durch ein gemeinsames Maß gemessen bzw. verglichen werden könnten. Ein solches Maß könnte nach ihrer Auffassung immer so gewählt werden, dass beide Größen als ganzzahlige Vielfache dieses Maßes darstellbar sind. Existiert zu zwei Größen ein solches Maß, dann heißen die Größen kommensurabel. Das größte gemeinsame Maß zweier Größen wird durch den EUKLIDischen Algorithmus bestimmt. Die dem EUKLIDischen Algorithmus zugrunde liegende Idee der Methode der Wechselwegnahme war vielen Handwerkern zu dieser Zeit schon lange bekannt. Da die Wechselwegnahme im Alltag immer zu einer Lösung führte, vermuteten die Phythagoreer, dass zwei beliebig gewählte, gleichartige Größen immer kommensurabel seien. Nachdem die Pythagoreer um ca. 500. v.Chr. die Mathematik als Wissenschaft begründet hatten, erfuhr sie kurz darauf bereits ihre erste Grundlagenkrise. Diese Krise wurde durch HIPPASOS VON METAPONT (ca. 5.Jhd. v. Chr.), einem Mann aus den eigenen Reihen, heraufbeschworen. Der Legende nach soll er am Pentagramm, dem Ordenssymbold der Pythagoreer, entdeckt haben, dass dessen Diagonale und Seitenlänge nicht kommensurabel sind. Da diese Entdeckung die Grundüberzeugung der Pythagoreer, dass sich „alles“ durch (natürliche) Zahlen repräsentieren läßt, in Frage stellte, sollen HIPPASOS Sektenbrüder ihn deshalb ins Meer geworfen bzw. die Götter sollen sogar sein Schiff zerschmettert haben. Die Endeckung inkommensurabler Größen ließ außerdem geometrische Beweise, die die Kommensurabilität für beliebige Größen voraussetzten, nichtig werden.
HIPPASOS´ Beweis soll hier nun dargelegt werden:
[Konvention: Mit AB bezeichne ich die Gerade, die durch die Punkte A und B geht.]

Betrachten wir die Seite e := ED und die Diagonale d := AC. e und d sind parallel zueinander, da im regelm. Fünfeck (Folge von 5 Punkten mit gleich langen Seiten und gleich großen Winkeln) jede Diagonale zu ihrer gegenüberliegenden Seite parallel sind. Dies liegt daran, dass das Fünfeck symmetrisch bspw. zur senkrechten Achse durch A ist, d.h., dass EB und DC senkrecht zu dieser Achse und damit parallel sind usw.
Wir versuchen nun Informationen über das Verhältnis von d zu e zu erfahren:
Da nun e und d und auch DB und EA parallel sind bilden die Punkte E, D, E´, A ein Parallelogramm P. Also ist auch e = AE´. Mit e´ := B´E´ = E´C (wieder regelm. Fünfeck) gilt also:
d = e + e´
Desweiteren ist e´´ := C´D´ = D´E´ (wieder regelm. Fünfeck, da ähnlich). Betrachten wir das Parallelogramm P´, welches durch die Punkte E, D´, C, D gebildet wird. Man sieht, dass e = D´C. Also:
e = e´ + e´´
Verfahren wir nun so weiter, so ergibt sich:
e´ = e´´ + e´´´,
e´´ = e´´´ + e´´´´
(...)
Das Verfahren endet nie, da wir immer wieder neue (ähnliche) Fünfecke finden (s. Zeichnung).
Also ist d : e (das Verhältnis einer Diagonalen zu einer Seitenlänge) irrational.
FRAGE: Welche (irrationale) Zahl repräsentiert denn nun d : e?
1. Methode (exakte Berechnung):
d/e = e/e´(da die Pentagramme ähnlich sind), e/d = e´/e = (d - e)/e = d/e - 1, d/e = e/d + 1. Mit x := d/e folgt: x = 1/x +1, x2 - x -1 = 0, x = (1 + \/5) / 2.
2. Methode (approximative Berechnung):
Approximation für v = 0:
d = e + r = 8u,In diesem Beispiel: d : e ≈ 8/5 = 1,6 [zum Vergleich: (1 + \/5) / 2 ≈ 1,6180].
Wie man sieht, ergeben die Koeffizienten von u gerade die sog. Fibbonacci-Folge [man füge noch eine 1 hinzu]. Von dieser weiß man, dass der Abstand zweier Folgenglieder, also auch der Wert d : e, gegen (1 + \/5) / 2 konvergiert.
ERGÄNZUNG: ÜBERTRAGUNG AUF QUADRATE
Dieses Verfahren kann man, wie in der letzten Vorlesung gesehen, auch auf Quadrate übertragen. Dort konnte man folgende Verhältnisse feststellen:
d = 1e + rNun Berechnung nach der approximativen Methode:
| r = 0 d = e d : e ≈ 1
|
s = 0 d = e + r = 3r e = 2r d : e ≈ 3/2= 1,5
|
t = 0 d = 1e + r = 7s e = 2r +s = 5s r = 2s d : e ≈ 7/5 = 1,4
|
u = 0 d = 1e + r = 17t e = 2r +s = 12t r = 2s + t = 5t s = 2t d : e ≈ 17/12 ≈ 1,4167
|
v = 0 d = 1e + r = 41u e = 2r +s = 29u r = 2s + t = 12u s = 2t + u = 5u t = 2u d : e ≈ 41/29 ≈ 1,4138 |
Wie man sieht nähern sich die Werte immer mehr \/2 an. Also kann man vermuten [und auch beweisen], dass im Quadrat d : e = \/2 : 1 gilt.
Zur vorangehenden
Stunde (05.12.03),
zur nächsten
Stunde (11.12.03),
zur Protokollübersicht.