Vorlesung Elementare Zahlentheorie WS 2003/04
Freitag, den 5.12.03 (AK)

kommutativer Ring-m-1: Monoid.

Hauptsatz der Arithmetik: Existenz von Zerlegung als Produkt von unzerlegbaren Elementen.

Eindeutigkeit von Zerlegung als Produkt von primen Elementen

R euklidischer Bereich (R, δ)

R kommutativer Integritätsbereich

Idee: a|b in R

a|echt b

Beh: Existenz von Zerlegung als Produkt von unzerlegbaren Elementen gilt in Euklidischen Bereichen.

Bew: (R, δ) euklidischer Bereich.

Ok, falls keine endliche Kette echter Teiler von a existiert.

...|a₂|a₁|a existiert.

Wenn eine solche Kette doch existiert, haben wir eine unendliche Kette

R>...W≥...>Ra₂>Ra₁>Ra von zyklischen Teilmodulen.

Bilde

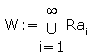
ist R-Teilmodul von R.

Etwa

,

(Widerspruch)

Fazit: Hauptsatz der Arithmetik gilt für Euklidische Bereiche.

R Ring-m-1

, ,

Teilmodul: „Linksideal“ , „Rechtsideal“ , „Ideal“ von R.

Zyklische Teilmodule: „Hauptideale“

Euklidische Bereiche sind Hauptidealbereiche.

Frage: Was ist ein „Größenbereich“?

z.B. der Größenbereich der Längen?

Physikalische existent: Stellen im Raum

1.Diskursebene

2.Diskursebene: „Kongruent“ ohne math. Definition sondern mithilfe geometrischer Vorstellung.

Was ist den Objekten gemeinsam?

Länge (abstrakt) rein theoretischer Begriff, kein physikalisches Objekt.

Längenbereich: Man kann addieren: komm.Gruppe

Vergleich: < Totalordnung

angeordnete Gruppe:

Zu 0<a<b existiert mit na>b (Archimedisches Axiom).

(R,>) ist archimedisch angeordnet.

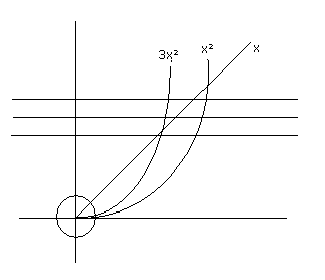
C_R konstante Funktion

(R[X],<)

f(0)=g(0)=0

X³<X²<X auf einem kleinen Intervall

X³<3X²<X

Definition: Ein Größenbereich ist eine archimedisch angeordnete (additiv geschreibene) abelsche Gruppe.

Angeordnete Gruppe: (G,+,0,-) Gruppe.

Anordnung (G,<) <: 1) Für gilt genau eine der folgende Aussagen: a<b, a=b, a>b.

2)Aus a<b, b<c folgt a<c.

Angeordnete Gruppe: Zusätzlich: Aus a<b folgt a+c<b+c.

Archimedisch angeordnete Gruppe: ... zu 0<a,b existiert mit b<na.

Hilfssatz: In einer angeordneten Gruppe haben alle Elemente ≠0 unendliche Ordnung.

Beweis: Angenommen, a≠0 hat doch endliche Ordnung n: na=0

1.Fall: a>0: 0<a<2a<3a<... na≠0.

2.Fall: a<0: analog.

Hilfssatz: In einer archimedisch angeordneten Gruppe haben wir „Division mit Rest“: zu 0<a,b existiert

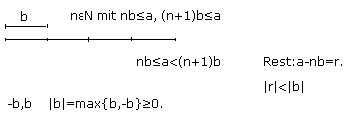
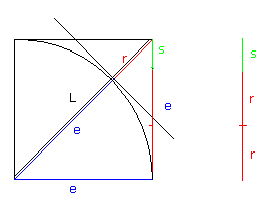
Q_e≤G Z_e≤G „Wechselwegnahme“

d=1e+r
e=2r+s
r=2s+t
s=2t+u
...

nicht endender EA!