Die Vorlesung beginnt mit einer kurzen Zusammenfassung der Themen aus den letzten Vorlesungen.

Dabei kommt die Frage auf, wie wir uns dabei fühlen, wenn wir über Einheitengruppen und Ähnliches sprechen. Diese Frage wird anscheinend mehrheitlich mit einer negativen Empfindung verbunden, was hauptsächlich dadurch zu begründen war, dass uns der Realitätsbezug und der Sinn unserer vorangegangenen Überlegungen fehlt.

Es stellt sich uns die Frage, warum wir das überhaupt wissen wollen. Warum machen wir das?

Diese Frage stellt sich auch häufig im Mathematikunterricht, wodurch wir eine Überleitung zur Schulsituation geschaffen haben. Wir stellen fest, dass die Schüler den Lehrer oft fragen, warum sie beispielsweise das Addieren lernen müssen, wo es doch Taschenrechner gibt. Den Schülern fehlt die Motivation – der Bezug zur Realität. Als Lehrer ist es jedoch unsere Aufgabe, die Schüler jeden Tag erneut zu motivieren. Es stellt sich also die Frage, ob die meisten Menschen in ihrem späteren Berufsleben überhaupt die Mathematik benötigen. Unsere Antwort auf diese Frage ist ein eindeutiges Ja, denn in allen Wissenschaften, beispielsweise der Chemie oder Biologie, aber auch in der Architektur oder im Rechtswesen wird die Mathematik ständig benötigt. Sei es um Statistiken zu erstellen oder zu lesen, Streitfragen zu klären, Populationen mithilfe des Räuber-Beute-Systems zu errechnen, oder sei es nur die Methodik, die das Fach Mathematik vermittelt.

Oft jedoch betreibt man Mathematik auch, weil es einfach nur „schön“ ist. Womit wir wieder zurück in der Universität, in unserer Vorlesung angekommen wären. Wir betreiben Mathematik also einfach momentan nur, weil sie schön ist. Bei uns ist der Satz, den wir gerade zu entwickeln versuchen, schön.

Zahlentheorie als solche ist ein Bereich der Mathematik, in dem es nur sehr wenige Anwendungen gibt und den man betreibt, weil es einem Spaß macht. Als ein Beispiel für eine Anwendung der Zahlentheorie werden letztendlich doch noch die Kryptosysteme (Verschlüsselung) gefunden. Mithilfe der Zahlentheorie können Nachrichten verschlüsselt werden (auch öffentlich), die von keinem Anderen als dem Empfänger entschlüsselt werden können.

Wir betreiben aber im Moment Mathematik und Zahlentheorie deshalb, weil es Spaß macht und weil die Methoden, die zur Lösung führen, schön sind.

Nach dieser kleinen Exkursion kehren wir zu unserem Stoff zurück.

Wir wollen einen Satz aufstellen:

.

1. Vermutung:

(schon gezeigt).

, (Beispiel:).

2. Vermutung:

.

Planung des weiteren Vorgehens:

- Frage: Was ist noch zu zeigen?

- Antwort: Die zweite Vermutung

- Plan: Beweis per vollständiger Induktion

Wir beschließen also, die zweite Vermutung mithilfe von Vollständiger Induktion zu beweisen.

Induktionsverankerung:

.

Induktionsannahme:

.

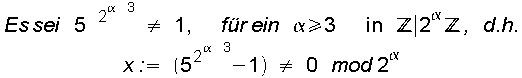Induktionsschritt:

.

Zu zeigen:

.

_______________________________________________________________________

Zwischenfrage:

Wir stellen fest, dass wir ein Problem haben. Wie bekommen wir also die Schwierigkeit in den Griff, dass wir uns in verschiedenen Restklassen befinden?

Um diese Frage zu beantworten, beschließen wir, uns erst einmal eine konkrete Vorstellung zu machen.

--> Topfrechnen.

Wir untersuchen, wie die Töpfe „Schlange“ und „Quer“ aussehen.

Wir stellen folgendes fest:

.

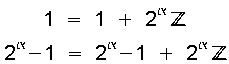
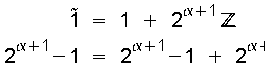Beim Vergleich der beiden Topfmengen können wir feststellen, dass der „Quer“-Topf doppelt so viele Elemente besitzt, wie der „Schlange“-Topf.

Zudem sind die Elemente des „Schlange“-Topfes im zugehörigen „Quer“-Topf enthalten.

Es lässt sich feststellen, dass jeder „Quer“-Topf in zwei „Schlange“-Töpfe zerfällt:

.

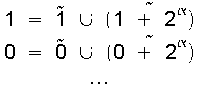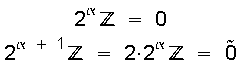, woraus sich ergibt, dass größer ist.

Jetzt wissen wir etwas mehr über die Struktur der Töpfe. Es ist üblich nicht mehr mit „Töpfen“ zu rechnen, sondern stattdessen Repräsentanten zu wählen.

Nun können wir mit der Vollständigen Induktion fortfahren.

_______________________________________________________________________

Wir haben:

Uns interessiert aber:

, bzw.

.

Wir wollen zeigen, dass

.

Wir wissen aber bereits:

.

Da sich y aus einer Summe zusammensetzt, deren zweiter Summand bereits nicht von geteilt wird, sollte nachgewiesen werden, dass der erste Summand geteilt wird von diesem Faktor, um sicher zu stellen, dass die gesamte Summe, somit also y, nicht von geteilt wird.

Wenn dies gezeigt ist, haben wir per Vollständiger Induktion die zweite Vermutung gezeigt.

Die letzte Überprüfung wird nach einigen verzweifelten Ansätzen auf die nächste Vorlesung verschoben.

Zum Seitenanfang,
zur vorangehenden Stunde (13.11.03),
zur Protokollübersicht,
zur nächsten Stunde (20.11.03).