§ 8 Pythagoräische Zahlentripel

I. Geschichte, Geometrie, Arithmetik 

Definition 1:   Ein PZT ist ein Tripel (x, y, z) aus drei natürlichen Zahlen x, y, z, die die  Gleichung x² +y ² = z² erfüllen.

Beispiel: (3, 4, 5) ist ein PZT, da 9 + 16 = 25 ist.  

Man kann ein PZT auf zwei Weisen betrachten:

- einerseits kann man es algebraisch deuten: und zwar als natürliches Lösungstripel der Gleichung x² + y ² = z² ;

- andererseits kann man es geometrisch deuten als pythagoreisches, d.h. rechtwinkliges Dreieck, kurz PD, mit den Katheten x und y und der Hypotenuse z.

Zur Geschichte:

Man weiß heute, dass schon vor ca. 4000 Jahren pythagoräische Zahlentripel bekannt waren und zwar bei den Babyloniern, also rund 1500 Jahre vor Pythagoras. Das älteste bekannte Zeugnis ist die rund 3800 Jahre alte so genannte babylonische Keilschrifttafel Plimpton 322 (Babylonier lebten in Mesopotamien – heutiger Irak- eine der ersten Hochkulturen). Sie wurde in der ersten Hälfte des 19. Jh. im Irak ausgegraben, und ihre erste Interpretation stammt aus dem Jahre 1935. Auf dieser Tafel sind 15 PZT aufgeschrieben, u.a.

(6480, 4961, 8161) und (13500, 12709, 18541). Dabei fällt auf, dass 8161 und 18541  Primzahlen sind. Da diese Tripel mit Sicherheit nicht durch bloßes Ausprobieren gefunden wurden, stellt sich nun die Frage 1), wie die Babylonier sie gefunden haben, und 2), wie man heute solche Tripel finden kann. 

(Zur Geschichte: QUELLE: http://hischer.de/uds/forsch/vortrag/hischer/ringvl02/funkbegr.pdf) 

Zu 2):    

2.1) Anwendungsbeispiel für die Schule 

Knotenschnur:

Man stellt den Schülern ein Brett und ein Seil mit zwölf Knoten in regelmäßigen Abständen zur Verfügung. Nun stellt man den Schülern die Aufgabe, auf dem Brett mit der Schnur ein PZT zu konstruieren. So entdecken die Schüler selbst, wie ein PZT entsteht. Bei zwölf Knoten gibt es dabei genau eine Möglichkeit.

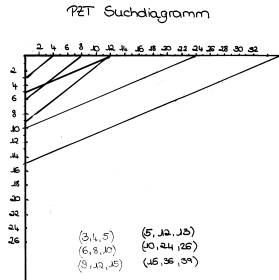
2.2) Anwendungsbeispiel

PZT-Suchdiagramm:           

In diesem Diagramm kann man mit Hilfe eines Lineals verschieden PZT finden. Dabei stellt man fest, dass man die PZT in Gruppen einteilen kann, wobei jeweils die Hypotenusen der Mitglieder einer Gruppe parallel sind. Das heißt also, dass die algebraische Operation „Multiplikation des Tripels oder der Gleichung mit einer natürlichen Zahl k“ geometrisch eine zentrische Streckung der Seitenlängen um das Zentrum C bedeutet.

Definition 2: Ein PZT (x, y, z) mit paarweise teilerfremden x, y, z heißt primitives PZT. 

Daraus folgt, dass man den kleinsten Vertreter jeder Gruppe von PZT primitiv nennt.

2.3) Geometrische Konstruktion:

Ein Quadrat mit seinem Inkreis

    T                                 S 

                                             M

        Q                    R

Um zum zweiten Tripel zu kommen benötigt man die Werte des ersten.

Man verbindet den linken unteren Eckpunkt des äußeren Quadrates mit Q  und erhält den Schnittpunkt M . Dann kann man das Tripel ablesen.

Dabei sind die Verhältnisse immer QR = 6/5 r und QS = 8/5 r (r Radius des Kreises).

Bei iterariver Fortsetzung der Reihe erhält man alle primitiven PZT.

2.4) Einheitskreis 

Zunächst stellt man die Anfangsgleichung des PZT so um, dass man eine Kreisgleichung für einen Einheitskreis erhält.

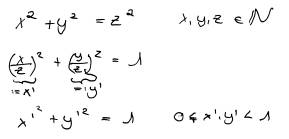
Dann kann man Werte für x´ und y´ berechnen. Diese Gleichung hat als Graphen den Viertelskreisbogen des Einheitskreises (ohne Endpunkte).

Genau die Punkte auf dem Viertelskreisbogen mit rationalen Koordinaten definieren ein PZT.

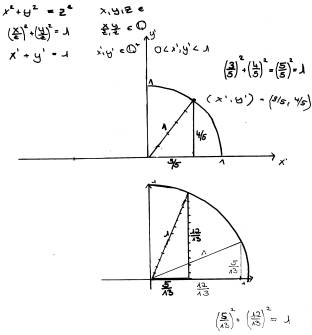
Wenn man so ausreichend viele Beispiele gefunden hat und diese alle in ein Achsenkreuz einträgt, erhält man einen Kreis. Diese Tatsache hat einen hohen architektonischen Wert. ...  

Frage: Warum kann ein gleichseitiges rechtwinkliges Dreieck mit Kathetenlänge x und Hypothenusenlänge y kein PZT definieren?

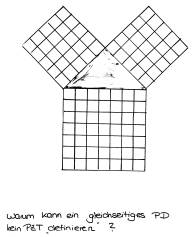
Als Ausgangsgleichung hat man x² + x² = y². Stellt man diese Gleichung um, so erhält man 2^1/2x = y. Daraus folgt, dass y keine rationale Zahl ist, also kein PZT definieren kann.

Frage: Wie kann man ein PZT algebraisch entwickeln?

Voraussetzung: eine Kathetenlänge ist gerade (x) und eine ist ungerade (y).

Zu zeigen: Es können nicht beide ungerade sein.

Beweis:  Angenommen, x und y sind ungerade.                  

Alternativbeweis: Angenommen, x und y sind ungerade.

(2n + 1)² + (2m + 1)²              = (2k)²

                        4n² + 4m + 1 + 4m² + 4m + 1 = 4k²

                        n² + n + m² + m + 0,5             = k²  

                                nicht in N                              in N             Widerspruch!

 Zu zeigen: x und y sind paritätsverschieden.

x² + y² = z²                              (1)

       y² = z² - x²                        (2)

       y² = (z – x)(z + x)               (3)

(z – x) und (z + x) sind beide gerade, also

    y²/4       =    (z + x)/2  * (z – x)/2          (4)

Quadratzahl              teilerfremd                      teilerfremd

Zu zeigen: (z + x)/2 und (z – x)/2 sind teilerfremd.

Beweis: Angenommen, g | (z + x)/2 und g | (z – x)/2.

Daraus folgt   g | (z + x + z – x)/2 und g | (z + x – z + x).

also   g | z                         und g | x.

Daraus folgt                  g | y                   (kein primitives PZT).

Frage: Wie berechnet man nun die Menge aller primitiven PZT?

Antwort:

(y/2)² = (z + x)/ 2 * (z – x)/ 2  

   c²    =     a²        *       b²

Dann ist z + x = 2a² und z – x = 2b².

Daraus folgt:   x = 2a² - z  und z = 2b² + x,

                also x = a² - b²   und z = a² + b² .

Aus (2) folgt dann   y² = (a² + b²)² - (a² - b²)² = 4a²b²,

                                 y = 2ab.

Behauptung:

Daraus folgt dann: Die Menge aller primitiven PZT ist

                                 L = {(x, y, z) in Z³ | (x, y, z) = (a² - b², 2ab, a² + b²) ; a, b in N,

                                        a > b, ggT(a, b) = 1, a und b paritätsverschieden}.