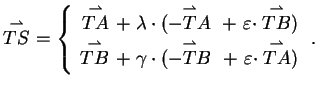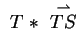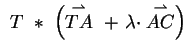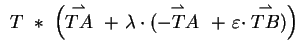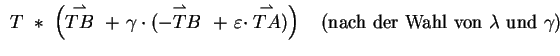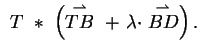Nächste Seite: Über dieses Dokument ...
Grundlagen der Geometrie
Protokoll vom 6. November 2000
1. Beweis der Strahlensätze (vgl. Vorlesung vom 2.11.2000).
Der Beweis erfolgt durch einen Ringschluss. Die erste Inklusion
 ist klar, da nach Voraussetzung
ist klar, da nach Voraussetzung  ist.
ist.
Die Inklusion
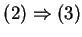 wird mit der gleichen Vorgehensweise wie
die Inklusion
wird mit der gleichen Vorgehensweise wie
die Inklusion
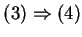 gezeigt.
gezeigt.
Beweisidee: Man suche sich zwei linear unabhängige Vektoren und
drücke die in der behauptung gesuchten Vektoren durch diese linear
unabhängigen aus. Kann
man dies auf zwei verschiedene Arten, so kann ein Koeffizientenvergleich
durchgeführt werden, der hoffentlich zu dem gesuchten Ziel führt.
Der Fall
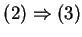 wird exemplarisch ausgeführt:
das Paar
wird exemplarisch ausgeführt:
das Paar
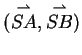 ist linear unabhängig. Mit den Eigenschaften des
affinen Raumes lässt sich der gesuchte Vektor
ist linear unabhängig. Mit den Eigenschaften des
affinen Raumes lässt sich der gesuchte Vektor
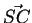 darstellen in der Form:
darstellen in der Form:
Für den Vektor
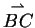 gilt aber auch
gilt aber auch
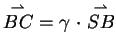 ,
da die
Punkte
,
da die
Punkte 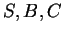 auf einer Geraden liegen. Diesen Zusammenhang in Gleichung
(1) eingesetzt führt zu:
auf einer Geraden liegen. Diesen Zusammenhang in Gleichung
(1) eingesetzt führt zu:
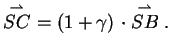 |
|
|
(2) |
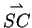 kann aber auch auf andere Weise ausgedrückt
werden:
kann aber auch auf andere Weise ausgedrückt
werden:
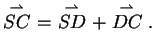 |
|
|
(3) |
Nach Voraussetzung gilt
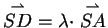 .
Die Seiten
.
Die Seiten 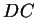 und
und 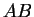 sind nach Voraussetzung parallel zueinander, so dass
für
sind nach Voraussetzung parallel zueinander, so dass
für
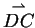 der Zusammenhang
der Zusammenhang
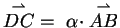 für einen
Skalar
für einen
Skalar 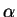 gilt. Der
Vektor
gilt. Der
Vektor
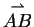 kann wiederum mit Hilfe der beiden linear
unabhängigen
Vektoren wie folgt ausgedrückt werden:
kann wiederum mit Hilfe der beiden linear
unabhängigen
Vektoren wie folgt ausgedrückt werden:
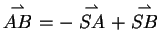 , so
dass sich insgesamt
, so
dass sich insgesamt
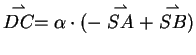 ergibt.
Durch
Einsetzen der Ausdrücke für
ergibt.
Durch
Einsetzen der Ausdrücke für
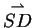 und
und
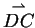 in Gleichung
(3) erhalten wir für
in Gleichung
(3) erhalten wir für
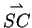 den Zusammenhang:
den Zusammenhang:
Der Koeffizientenvergleich in den Gleichungen (2) und (4)
führt zu
und Einsetzen des Koeffizienten 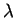 in Gleichung (2) führt zu
der Behauptung
in Gleichung (2) führt zu
der Behauptung
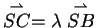 .
.
Mit einer analogen Vorgehensweise erhält man aus Voraussetzung (3) auch die
Behauptung (4). Der Ringschluss schließlich von (4) nach (1) ist wieder
klar, da die Behauptung 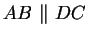 direkt aus der Voraussetzung (4) folgt.
direkt aus der Voraussetzung (4) folgt.
2. Beweis des Parallelogrammsatzes
Auch hier benutzten wir die gleiche Vorgehensweise wie im Beweis des
Strahlensätze. Als Paar von linear unabhängigen Vektoren wählen wir
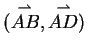 . Der Vektor
. Der Vektor
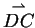 kann auf verschiedene Arten
ausgedrückt werden:
kann auf verschiedene Arten
ausgedrückt werden:
für einen Skalar 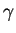 .
Durch Koeffizientenvergleich erhält man
.
Durch Koeffizientenvergleich erhält man 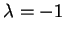 und
und 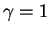 , was
zur Behauptung
, was
zur Behauptung
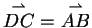 führt.
führt.
3. Satz von Veblen und Young (alt)
Satz: Gegeben sei ein affiner Raum (im Sinne der LA I) über einem
Vektorraum 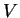 und ein Viereck
und ein Viereck 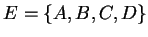 , wobei das Seitenpaar
, wobei das Seitenpaar 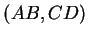 nicht windschief und auch das Seitenpaar
nicht windschief und auch das Seitenpaar 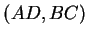 nicht windschief ist.
nicht windschief ist.
Behauptung: Dann ist auch das Seitenpaar 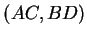 nicht windschief.
nicht windschief.
Beweis: 1. Fall: 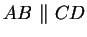 und
und 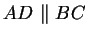 .
.
Wir wollen zeigen, dass sich die beiden Seiten schneiden oder parallel sind (und
somit nicht windschief sind). Dazu muss die Frage beantwortet werden: existieren
Elemente
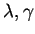 im Schiefkörper
im Schiefkörper 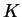 , so dass für den Schnittpunkt
, so dass für den Schnittpunkt 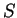
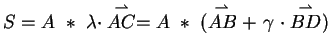 |
|
|
(7) |
gilt? Um Kandidaten für 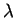 und
und 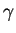 zu bekommen, führen wir
zunächst eine Analyse durch. Wenn
zu bekommen, führen wir
zunächst eine Analyse durch. Wenn 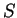 existiert, dann gilt für
existiert, dann gilt für 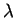 und
und
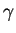 folgendes:
folgendes:
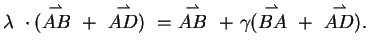 |
|
|
(8) |
Umsortieren der Gleichung führt zu
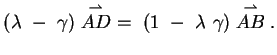 |
|
|
(9) |
Da das Paar
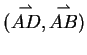 linear unabhängig ist, gilt für die Skalare
linear unabhängig ist, gilt für die Skalare
Nun werden zwei Fälle betrachtet.
Fall (a): In unseren Körper 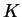 ist
ist 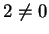 . Dann setzen wir
. Dann setzen wir
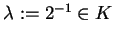 und
und
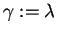 .
.
Fall (b): In unserem Körper 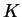 gilt
gilt 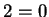 . Es ist zu zeigen, dass
. Es ist zu zeigen, dass
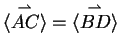 ist. Wir wissen, dass gilt:
ist. Wir wissen, dass gilt:
Aus der ersten Gleichung folgt, dass
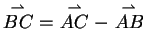 ist. Diesen
Zusammenhang in die zweite Gleichung eingesetzt ergibt
ist. Diesen
Zusammenhang in die zweite Gleichung eingesetzt ergibt
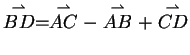 , woraus, wegen der Gleichheit
, woraus, wegen der Gleichheit
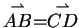 der gesuchte Zusammenhang
der gesuchte Zusammenhang
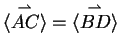 folgt.
folgt.
Das heißt, es existieren solche gesuchten 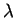 und
und 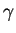 , für die die
Gleichung (8) erfüllt ist.
, für die die
Gleichung (8) erfüllt ist.
Für die Durchführung des Beweises wählen wir nun 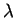 und
und 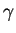 wie
in der Analyse berechnet und bilden
wie
in der Analyse berechnet und bilden
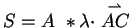 . Daraus
folgt, dass der Punkt
. Daraus
folgt, dass der Punkt 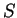 auf der Seite
auf der Seite 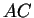 liegt, also
liegt, also 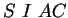 . Der Vektor
. Der Vektor
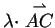 kann auch dargestellt werden
durch den Zusammenhang
kann auch dargestellt werden
durch den Zusammenhang
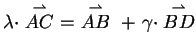 ,
woraus für den Punkt
,
woraus für den Punkt 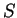 folgt:
folgt:
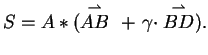 |
|
|
(14) |
Andererseits ist
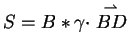 und
somit gilt
und
somit gilt 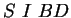 . Das bedeutet, dass
. Das bedeutet, dass 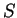 auf
beiden Seiten liegt, und es folgt:
auf
beiden Seiten liegt, und es folgt:
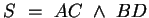 .
.
2.Fall: 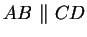 und
und
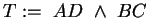 existiert.
existiert.
Wir führen zunächst eine Analyse durch: Das Paar
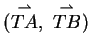 ist linear unabhängig und deshalb
drücken wir alle Vektoren mit Hilfe dieser beiden aus. In dieser Analyse
nehmen wir an, dass der Schnittpunkt
ist linear unabhängig und deshalb
drücken wir alle Vektoren mit Hilfe dieser beiden aus. In dieser Analyse
nehmen wir an, dass der Schnittpunkt
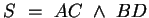 existiert. Dann kann
der Vektor
existiert. Dann kann
der Vektor
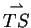 für geeignete Skalare
für geeignete Skalare
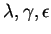 folgendermaßen geschrieben werden:
folgendermaßen geschrieben werden:
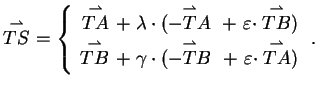 |
|
|
(15) |
Dabei gilt
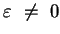 , da sonst die Punkte
, da sonst die Punkte 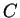 und
und 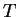 zusammenfallen, und außerdem ist
zusammenfallen, und außerdem ist
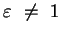 , da sonst
, da sonst 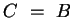 gilt. Der Vergleich der Koeffizienten führt zu:
gilt. Der Vergleich der Koeffizienten führt zu:
Also
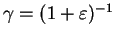 und
und
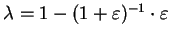 .
.
Der Fall
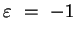 muss gesondert betrachtet werden. Nach der
Voraussetzung sind die Seitenpaare
muss gesondert betrachtet werden. Nach der
Voraussetzung sind die Seitenpaare 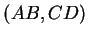 und
und 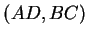 jeweils nicht
windschief. Der Punkt
jeweils nicht
windschief. Der Punkt 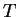 ist nun aber der Schnittpunkt der Diagonalen, so dass
auch das Seitenpaat
ist nun aber der Schnittpunkt der Diagonalen, so dass
auch das Seitenpaat 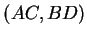 nicht windschief und somit die Behauptung des
Satzes erfüllt ist.
nicht windschief und somit die Behauptung des
Satzes erfüllt ist.
Für den eigentlichen Beweis wird der Spieß umgedreht und die
Analyse rückwärts betrachtet. Wir wählen also die Skalare
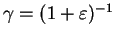 und
und
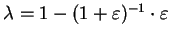 . Dann bilden wir
. Dann bilden wir
Das bedeutet, dass 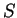 sowohl auf der Seite
sowohl auf der Seite 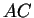 , als auch auf
, als auch auf 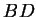 liegt. Also
ist
liegt. Also
ist 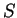 der Schnittpunkt der beiden Seiten und die Behauptung ist bewiesen.
der Schnittpunkt der beiden Seiten und die Behauptung ist bewiesen.



Nächste Seite: Über dieses Dokument ...
Eva
2000-11-27
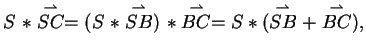
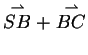
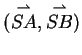 ist linear unabhängig. Mit den Eigenschaften des
affinen Raumes lässt sich der gesuchte Vektor
ist linear unabhängig. Mit den Eigenschaften des
affinen Raumes lässt sich der gesuchte Vektor
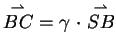 ,
da die
Punkte
,
da die
Punkte 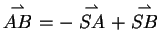 , so
dass sich insgesamt
, so
dass sich insgesamt
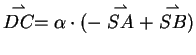 ergibt.
Durch
Einsetzen der Ausdrücke für
ergibt.
Durch
Einsetzen der Ausdrücke für
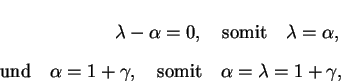
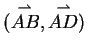 . Der Vektor
. Der Vektor
![]() kann auf verschiedene Arten
ausgedrückt werden:
kann auf verschiedene Arten
ausgedrückt werden:
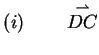
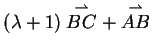
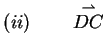
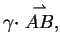
![]() und ein Viereck
und ein Viereck ![]() , wobei das Seitenpaar
, wobei das Seitenpaar ![]() nicht windschief und auch das Seitenpaar
nicht windschief und auch das Seitenpaar ![]() nicht windschief ist.
nicht windschief ist.
![]() nicht windschief.
nicht windschief.
![]() und
und ![]() .
.
![]() im Schiefkörper
im Schiefkörper ![]() , so dass für den Schnittpunkt
, so dass für den Schnittpunkt ![]()
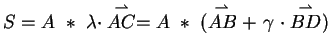
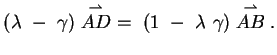
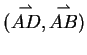 linear unabhängig ist, gilt für die Skalare
linear unabhängig ist, gilt für die Skalare
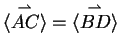 ist. Wir wissen, dass gilt:
ist. Wir wissen, dass gilt:
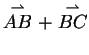
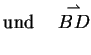
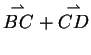
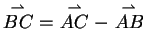 ist. Diesen
Zusammenhang in die zweite Gleichung eingesetzt ergibt
ist. Diesen
Zusammenhang in die zweite Gleichung eingesetzt ergibt
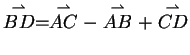 , woraus, wegen der Gleichheit
, woraus, wegen der Gleichheit
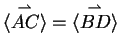 folgt.
folgt.
![]() und
und ![]() wie
in der Analyse berechnet und bilden
wie
in der Analyse berechnet und bilden
![]() . Daraus
folgt, dass der Punkt
. Daraus
folgt, dass der Punkt ![]() auf der Seite
auf der Seite ![]() liegt, also
liegt, also ![]() . Der Vektor
. Der Vektor
![]() kann auch dargestellt werden
durch den Zusammenhang
kann auch dargestellt werden
durch den Zusammenhang
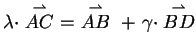 ,
woraus für den Punkt
,
woraus für den Punkt ![]() folgt:
folgt:
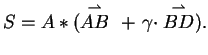
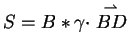 und
somit gilt
und
somit gilt ![]() und
und
![]() existiert.
existiert.
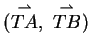 ist linear unabhängig und deshalb
drücken wir alle Vektoren mit Hilfe dieser beiden aus. In dieser Analyse
nehmen wir an, dass der Schnittpunkt
ist linear unabhängig und deshalb
drücken wir alle Vektoren mit Hilfe dieser beiden aus. In dieser Analyse
nehmen wir an, dass der Schnittpunkt
![]() existiert. Dann kann
der Vektor
existiert. Dann kann
der Vektor
![]() für geeignete Skalare
für geeignete Skalare
![]() folgendermaßen geschrieben werden:
folgendermaßen geschrieben werden: