Grundlagen der Geometrie
Protokoll vom 25.01.01 (FM)

Zunächst untersuchten wir in Fortsetzung der vorangegangenen Vorlesung den Begriff des Kreises.

Als Kreis um den Mittelpunkt M mit dem Radius (M, A) hatten wir die Menge der Punkte P definiert, die den gleichen Abstand zu M haben wie A:
K(M, (M, A)):= {P | (M, P) º (M, A)}.
Zu untersuchen war nun, ob Kreise "anständig" sind, das heißt, ob für einen beliebigen Punkt A' auf dem Kreis K(M, (M, A')) = K(M, (M, A)) gilt.
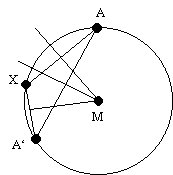
Zwei Punkte haben den gleichen Abstand zu einem dritten Punkt, wenn dieser auf der Mittelsenkrechten ihrer Verbindungsgeraden liegt. Für drei Punkte A, A' und X auf einem Kreis ergibt sich damit die folgende Konstruktion mit dem Dreieck (A, A', X).

Wir mußten feststellen, das wir in unseren Überlegungen die Möglichkeit der Existenz isotroper Geraden nicht beachtet hatten. Diese Tatsache motivierte die folgende Untersuchung im Rahmen der Analytischen Geometrie.

Wir betrachten die affine Ebene zu einem zweidimensionalen R-Vektorraum mit einem nicht ausgearteten Skalarprodukt. Nach dem Satz von Sylvester besitzt diese Matrix eine Orthonormalform. Diese Matrix kann entweder positiv definit, die Normalform also gleich  sein, oder nicht positiv definit, die Normalform also gleich  sein.
Das Skalarprodukt definiert eine Orthogonalitätsrelation auf der affinen Ebene. Ist das Skalarprodukt positiv definit, so erhalten wir eine Euklid-Ebene ohne isotrope Richtungen. Ist es nicht positiv definit, so ergibt sich eine Minkowski-Ebene mit genau zwei isotropen Richtungen.

Kreise veranschaulichen wir vor dem Hintergrund einer euklidischen Zeichenebene je nach Art des Skalarproduktes unterschiedlich:
 

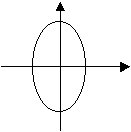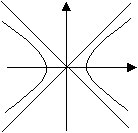Euklid-Ebene	Minkowski-Ebene

[Die Form der "Ellipse" ergibt sich aus der Tatsache, daß wir den Begriff der Abstandsgleichheit auf Koordinatenachsen noch nicht eingeführt haben. Ebenso braucht im Minkowski-Fall keine gleichseitige "Hyperbel" zu entstehen.]

[Zum Kreisbegriff siehe Stunde vom 22.01.01.]

Die Begriffe der Orthogonalität und des Kreises legten die Untersuchung des Thales- Phänomens nahe.

Satz:
Gegeben sei eine affine Ebene mit (F), (D), der Orthogonalitätsrelation ^ mit (O1) bis (O4) sowie den äquivalenten Aussagen (H), (M) und (K). Weiterhin sei ein Kreis K = K(M, (M, A)) gegeben. Dann sind die folgenden Aussagen äquivalent.
(1) P Î K.
(2) PA ^ PB.

Beweis:
P liegt auf K genau dann, wenn (M, P) abstandsgleich zu (M, A) ist.
Dies ist laut Definition genau dann der Fall, wenn M auf der Mittelsenkrechten von (A, P) liegt.
[Den Punkt X definieren wir als den Mittelpunkt von (A, P). Die Gerade XM) ist also orthogonal zu AP, wenn P auf dem Kreis liegt.]

Dieser Bewies scheint aufgrund seiner Einfachheit durchaus auch für den Schulunterricht geeignet.

Eine andere Vorgehensweise stellt der Didaktiker M. Wagenschein (Wirkungszeit ca. 1960 - 85) in einem Aufsatz vor.
Sein Ziel ist das ursprüngliche Verstehen der Schüler, in seinen Augen selbstverständliche Annahmen wie (O1) bis (O4) sollen seiner Meinung nach nicht explizit erarbeitet werden. Er ist ein Verfechter der heuristischen Methode, sieht den Lehrer als denjenigen an, der seine Schüler "nur" vom Ufer aus auf seinem Weg leitet.
[Literaturhinweise:
M. Wagenschein, Entdeckung der Axiomatik, MU 20:1 (1974), S. 52 - 70; HB: Z5577-20.
L. Führer, Pädagogik des Mathematikunterrichts: eine Einführung in die Fachdidaktik für Sekundarstufen, Vieweg (1997), ISBN 3-528-06911-2, S. 224--230, insbesondere 229--230; HB: Bb553].

Seine Vorstellung vom Beweis des Satz des Thales gliedert sich in die folgenden Schritte.

• Die Radien (M, A), (M, B) und (M, P) werden eingezeichnet.
• Dadurch wird der Winkel bei P in zwei ungleiche Winkel a und b geteilt.


• Da das Phänomen von nun an nur an dem Dreieck betrachtet wird, wird die "überflüssige" Kreislinie weggewischt.
• Durch die Einzeichnung des Radius (M, P) sind zwei gleichschenklige Dreiecke entstanden, deren Basiswinkel jeweils gleich sind.
• Die Faltkniffe der symmetrischen Dreiecke werden eingezeichnet.
• Nun wird ein zweites Dreieck (A', B', P') eingezeichnet, indem das ursprüngliche Dreieck so verschoben wird, daß A' gleich B ist.


• Durch Einzeichnen der Strecke (P, P') entsteht ein drittes deckungsgleiches Dreieck in der Mitte, in das ebenfalls die bisher bekannten Winkelbezeichnungen eingetragen werden.
• Der Schüler soll nun erkennen, daß die Winkel bei B die Gleichung 2a + 2b = 180 ° erfüllen. 180 ° bezeichnet hier eine halbe Umdrehung.
• Damit beträgt der Winkel bei P die Summe a + b = 90°, der Satz ist bewiesen.

• Der Halbkreis als wesentlicher Bestandteil des geometrischen Phänomens fehlt im abschließenden Tafelbild. Statt des Wegwischens des Kreises sollte eine neue Zeichnung angefertigt werden und damit die ursprüngliche Darstellung des Phänomens an der Tafel erhalten bleiben.
• Es ist sehr unwahrscheinlich, daß die Idee der Translation von den Schülern selbst initiiert wird.
• Die Einführung von Winkelmaßen verlagert die geometrische Betrachtung zu einer schließlich rein rechnerischen Lösung.

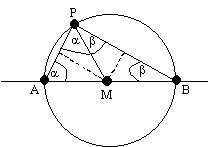
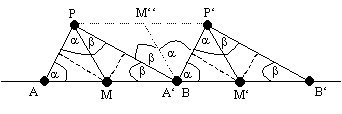
Um den Begriff der Winkelhalbierenden genauer untersuchen zu können, führten wir zwei Definitionen ein.

Definition: Ein Tripel (S, g, h) mit S I g und S I h [Man beachte: g = h ist zugelassen !] nennen wir Geradenkreuzung.
[Anmerkung: Zu einem späteren Zeitpunkt haben wir die Schreibweise (S, {g, h}) für eine Geradenkreuzung eingeführt.]

Definition: Eine Gerade m heißt Halbierende der Geradenkreuzung (S, g, h), wenn g durch eine Spiegelung s an m auf h abgebildet wird. [Hierbei darf m keine isotrope Gerade sein.]

Aus einer Zeichnung ließ sich direkt der folgende Satz erkennen.
Satz: Existiert eine Halbierende m, so auch eine weitere Halbierende m', die orthogonal zu m ist.