Explanation
Some years ago the Nikolaus webpage has shown all possibilities to draw the
"Haus des Nikolaus" ("house of Santa Claus") without lifting the
pencil off the paper, for example
like this 
or
like this 
.
In this puzzle you must count the number of possibilities to draw this and some other figures in this way. Before giving the puzzles we must explain how we want to count the solutions. The figures are given as follows:
(a) 
(b) 
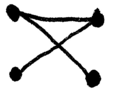(c)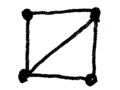 
Only whole lines connecting the nodes (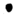
)
must be drawn (no turns at crossings of lines). If we have one solution we can
also reverse it, we consider this as the same solution. Furthermore, if we have
a circuit as solution (i.e., it starts and ends in the same point), we
consider solutions which follow the same sequence of lines only from another
starting point as the same solution. So, for each of the two example
figures (a) and (b) above we say that the number of possibilities to
draw them without lifting the pencil is 1. In case (c) the number of
possibilities is 6.
The puzzle
To solve the puzzle you have to find the number of possibilities to draw each of the following seven figures (d)-(j) without lifting the pencil (counted as explained above). You only see one of the figures at a time. You need to enter the correct solution before seeing the next. Click here to start with figure (d).