




Next: Abbildungsverzeichnis
Up: Konstruktionen
Previous: 1869-dimensionale Darstellung von über
Inhalt
Index
56-Dimensionaler Modul von 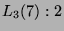
Nach [CCN$^$85] ist
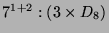 eine maximale
Untergruppe von
eine maximale
Untergruppe von 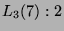 von Index 57 und es gilt
von Index 57 und es gilt
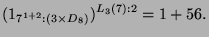 |
(4.14) |
Sei die Gruppe
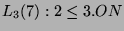 gegeben als Erzeugnis von
Permutationen auf 465 Punkten:
gegeben als Erzeugnis von
Permutationen auf 465 Punkten:
Dies entspricht der Permutationsoperation von 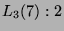 auf den
Nebenklassen von
auf den
Nebenklassen von
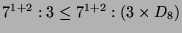 und es gilt
und es gilt
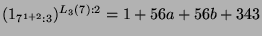 . Über
. Über 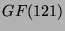 lassen sich die beiden 56-dimensionalen Konstituenten der
Permutationsdarstellung realisieren. Mit dem MeatAxe-Programm
chop erhält man somit über
lassen sich die beiden 56-dimensionalen Konstituenten der
Permutationsdarstellung realisieren. Mit dem MeatAxe-Programm
chop erhält man somit über 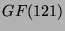 eine
56-dimensionale Darstellung von
eine
56-dimensionale Darstellung von 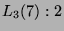 .
.
Markus Ottensmann
2000-02-10
![]() eine maximale
Untergruppe von
eine maximale
Untergruppe von ![]() von Index 57 und es gilt
von Index 57 und es gilt
![]() gegeben als Erzeugnis von
Permutationen auf 465 Punkten:
gegeben als Erzeugnis von
Permutationen auf 465 Punkten: