Grundlagen der Geometrie
Protokoll der Übungsstunde vom 10.01.01 (AS)

In der Übung wurden die Aufgaben 21 und 22 von Aufgabenblatt 8 und 9 besprochen.
 

Aufgabe 21
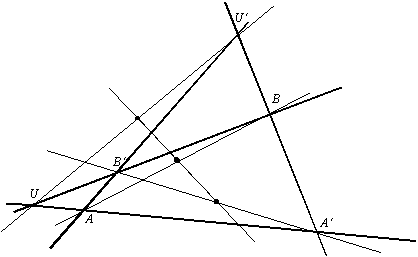
In einer affinen Ebene sei ein Vierseit mit sechs Ecken  (A, A', B, B', U, U') gegeben (vgl. Skizze). Drei Paare von Ecken sind noch nicht verbunden.
Untersucht werden soll die gegenseitige Lage der drei Mittelpunkte dieser drei Paare von Gegenecken.

Zunächst wurde eine Skizze angefertigt (experimentelle Untersuchung).

Die Vermutung, dass in einer affinen Ebene über einem K-Vektorraum (K Körper) die Mittelpunkte auf einer Geraden liegen, wurde nun mit Mitteln der Analytischen Geometrie bewiesen. Für die vektorielle Darstellung der Eckpunkte wählten wir U als Ursprung. Wir definierten Ortsvektoren für die Eckpunkte durch folgende Gleichungen:
A = U * a, A' = U * a' usw.
Die Ortsvektoren der Mittelpunkte der drei Paare von Ecken, die noch nicht verbunden sind ({U, U'}, {A, B}, {A', B'}), sehen dann folgendermaßen aus:
, , .

Diese sollen in der Basis (a, b) ausgedrückt werden. Dort ist a' := aa mit a Î K \ {0, 1} und b' := bb mit b Î K \ {0, 1}.
Zur Berechnung von u' stellten wir das Gleichungssystem u' = a + m (b' - a) und u' = l (a' - b) mit m, lÎ K \ {0, 1} auf.
Gleichsetzen der der rechten Seiten und Ersetzen von a' und b' ergibt nach Umformung
(1 -  m) a + m b b = l aa + (1 - l) b.
Mittels Koeffizientenvergleich [a und b sind linear unabhängig] erhält man
m (1 - b a) = 1 - a. [ba ist ungleich 1, da sonst a = 1 folgen würde.]
Daraus folgt: m = (1 - a) (1 - b a)^-1 und u' = a + (1 - a) (1 - b a)^-1 (b b - a).

Es bleibt noch zu zeigen, dass die Mittelpunkte mit den Ortsvektoren
,
,

auf einer Geraden liegen, d. h. dass die Differenzen  und   linear abhängig sind.
Wir prüften hierzu, ob
und

linear abhängig sind.
Mit  gilt
.
Der Koeffizientenvergleich zeigt, dass x und y linear abhängig sind, wenn man (1 - a)^-1 und (b - 1) vertauschen kann, d. h. wenn der Körper kommutativ ist.
Daraus folgt, dass die drei Mittelpunkte von drei Eckenpaaren eines Vierseits auf einer Geraden  [der Gauß - Geraden] liegen, wenn das Pappus-Axiom (P) vorausgesetzt wird.

Der Beweis mit Hilfe der Axiome (synthetischer Beweis) wurde nicht durchgeführt.
 

Aufgabe 22
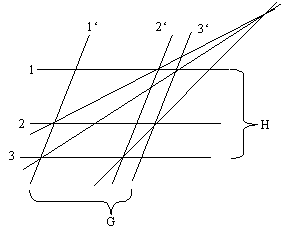
(pP*): Gegeben sei eine projektive Ebene mit zwei Punkten G und H. Durch G gehen  drei Geraden 1', 2' und 3' und durch H drei Geraden 1, 2 und 3.
Dann schneiden sich die drei Geraden durch die Schnittpunkte von 1 mit 2' und 2 mit 1',  von 1 mit 3' und 3 mit 1' sowie  von 2 mit 3' und 3 mit 2' in einem Punkt, dem Pappus-Punkt (vgl. Skizzen).
  Die Lage des Pappus-Punktes ist abhängig von der gewählten Benennung der Geraden, es ergeben sich 6 Möglichkeiten.
Die gegenseitige Lage dieser Pappus-Punkte wurde nicht in der Übungsstunde untersucht.
Aufgabenteil c) wurde nicht besprochen.