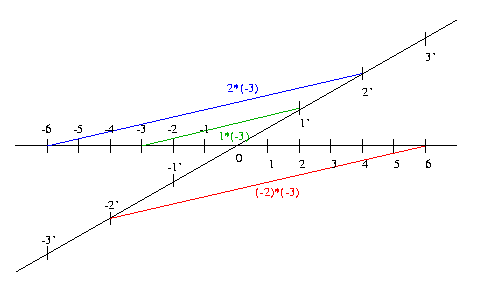
Gegeben ist eine affine Ebene mit (F) und (P) sowie zwei Geraden mit 0- und 1-Punkten (damit sind dann Skalen auf den Geraden gegeben).

Man kann dann 1 * (-3) als Verbindungsgerade der Punkte 1' und -3 (grün) einzeichnen. Die Parallele durch den Punkt 2' (blau) ist 2 * (-3) und geht durch den Punkt -6 (als Ergebnis). Als weitere Parallele durch -2' geht (-2) * (-3) (rot) durch den Punkt 6 = (-2) * (-3).
(Voraussetzungen wie in a).)
Zwischenbemerkung: AdditionDie Addition von zwei Punkten a, b wird durch die Verschiebung (rot) des Punktepaars (0,b) auf die gepunktete Parallele auf das Punktepaar (0',b'). Dieses wird dann so verschoben (grün), daß 0' auf a landet. b' wird dann auf a + b verschoben. 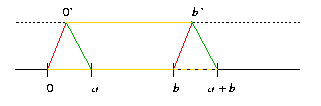 |
Wir wollen jetzt das Distributivgesetz a * (b + c) = a * b + a * c zeigen:
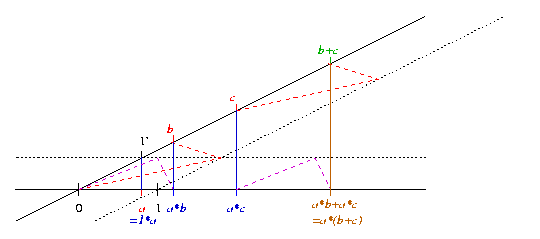
Als erstes wird a * (b + c) gebildet, indem b und c addiert werden (rot gestrichelt). Für die Multiplikation wird eine Gerade durch 1' und a (blau) gelegt. Die Parallele durch b + c (braun) ergibt a * (b + c). Im nächsten Schritt wird a * b + a * c ermittelt. Dazu werden die Parallelen zu 1'a durch b und c (ebenfalls blau) gelegt. Die so erhaltenen Punkte a * b und a * c werden dann addiert (violett gestrichelt). Der so erhaltene Punkt a * b + a * c ist gleich dem Punkt a * (b + c).
Nun soll das Assoziativgesetz bei der Addition (a + b) + c = a + (b + c) nachgewiesen werden:
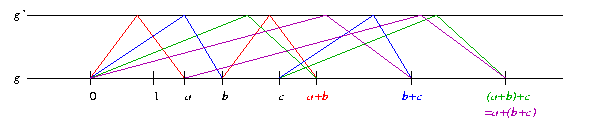
Wir wollen als erstes den Punkt (a + b) + c bilden. Dazu addieren wir zuerst a und b
(rot) und erhalten den Punkt a + b. Dann addieren wir a + b und c (grün) und
erhalten den Punkt (a + b) + c. Jetzt wird a + (b + c) ermittelt. Wir addieren b und
c und bekommen den Punkt b + c (blau). Diesen Punkt addieren wir zu a (violett) und
erhalten den Punkt a + (b + c) der der gleiche Punkt wie (a + b) + c ist.