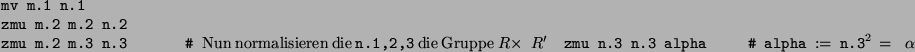Die Untergruppe
![]() hat die Ordnung 64. Nach [O'N96, Bemerkung nach
Lemma 5.7, Seite 448] existiert in
hat die Ordnung 64. Nach [O'N96, Bemerkung nach
Lemma 5.7, Seite 448] existiert in ![]() eine Untergruppe der
Ordnung 32, die
eine Untergruppe der
Ordnung 32, die
![]() normalisiert.
normalisiert.
![]() hat 1992 Bahnen auf 122
hat 1992 Bahnen auf 122![]() 760 Punkten. Sei
760 Punkten. Sei
![]() die
Operation von
die
Operation von ![]() eingeschränkt auf eine Bahn der Länge 64. In GAP
findet man sieben Normalteiler von Index zwei in
eingeschränkt auf eine Bahn der Länge 64. In GAP
findet man sieben Normalteiler von Index zwei in
![]() . Bildet man die Urbilder dieser Normalteiler, so sieht
man, daß nur eines dieser Urbilder
. Bildet man die Urbilder dieser Normalteiler, so sieht
man, daß nur eines dieser Urbilder ![]() die Gruppe
die Gruppe
![]() normalisiert. In GAP kann man die Erzeuger des berechneten
Normalteilers
normalisiert. In GAP kann man die Erzeuger des berechneten
Normalteilers ![]() in die Erzeuger von
in die Erzeuger von
![]() faktorisieren:
faktorisieren:
![]()
Damit folgt, daß für
![]() ,
,
![]() ,
,
![]()
Das Element
![]() (von Ordnung 2) operiert auf
(von Ordnung 2) operiert auf ![]() durch Invertieren der Erzeuger und auf
durch Invertieren der Erzeuger und auf ![]() operiert
operiert ![]() trivial. Zur
Bestimmung von ,,
trivial. Zur
Bestimmung von ,,
![]() `` wird eine zentrale Involution
benötigt, Element der Ordnung zwei, das wie ,,
`` wird eine zentrale Involution
benötigt, Element der Ordnung zwei, das wie ,,![]() `` auf
`` auf
![]() operiert. Man sieht, daß das Element
operiert. Man sieht, daß das Element
![]() die gewünschte Eigenschaft hat. Man beachte, daß
die gewünschte Eigenschaft hat. Man beachte, daß
![]() das Zentrum der
Ordnung vier von
das Zentrum der
Ordnung vier von ![]() ist.
ist.
Das folgende Script berechnet n.1![]() , n.2
, n.2![]() , n.3
, n.3![]() und alpha
und alpha![]() mit der
MeatAxe:
mit der
MeatAxe: