




Next: Bestimme eine Untergruppe des
Up: Die sechste maximale Untergruppe
Previous: Bestimme
Inhalt
Index
In
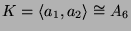 findet man die folgenden
Elemente der Ordnung 3:
findet man die folgenden
Elemente der Ordnung 3:
Mit GAP kann man nachrechnen, daß
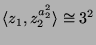 . Desweiteren sieht man, daß
. Desweiteren sieht man, daß 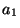 auf
auf
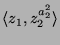 durch Invertieren der Erzeuger operiert. Sei
durch Invertieren der Erzeuger operiert. Sei
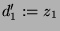 und
und
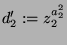 , so ist
und
, so ist
und 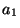 normalisiert
normalisiert 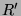 .
.
Markus Ottensmann
2000-02-10
![]() findet man die folgenden
Elemente der Ordnung 3:
findet man die folgenden
Elemente der Ordnung 3: