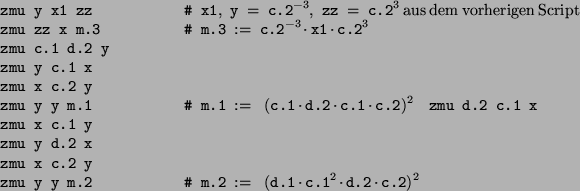Bestimme nun den vollen Normalisator
![]() .
.
Nach [CCN$^$85, ![]() , Seite 23] gilt
, Seite 23] gilt
Nach der obigen Konstruktion ist bekannt, daß
![]() , für
, für ![]() aus
(4.5). Desweiteren ist bekannt, daß
aus
(4.5). Desweiteren ist bekannt, daß ![]() durch
durch
![]() normalisiert wird. Durch Randomsuche in GAP
findet man zwei weitere Elemente der Ordnung 4 bzw.8 in
normalisiert wird. Durch Randomsuche in GAP
findet man zwei weitere Elemente der Ordnung 4 bzw.8 in
![]() , die
, die ![]() normalisieren:
normalisieren:
Das folgende Script berechnet m.1![]() , m.2
, m.2![]() und m.3
und m.3![]() mit der MeatAxe:
mit der MeatAxe: