




Next: Bestimme
Up: Die sechste maximale Untergruppe
Previous: Bestimme
Inhalt
Index
Nun bestimme eine Untergruppe
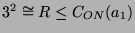 , die von
, die von
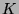 zentralisiert wird. Nach (4.2) gilt dann
zentralisiert wird. Nach (4.2) gilt dann
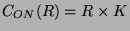 .
.
Nach [CCN$^$85, 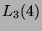 , Seite 23] gilt
, Seite 23] gilt
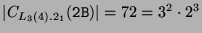 und
und
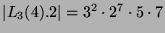 , also folgt
, also folgt
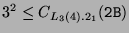 . Suche also ein 2B-Element in
. Suche also ein 2B-Element in
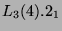 und suche im Zentralisator
und suche im Zentralisator
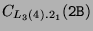 Elemente der Ordnung 3.
Elemente der Ordnung 3.
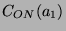 hat neun Bahnen auf den Punkten
hat neun Bahnen auf den Punkten
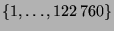 . Sei
. Sei 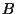 die Bahn der Länge 120. Dann ist
die Bahn der Länge 120. Dann ist
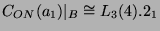 . Sei
. Sei
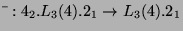 die Einschränkung auf die Bahn
die Einschränkung auf die Bahn 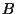 . Dann gilt
. Dann gilt
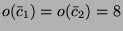 . Sei
. Sei
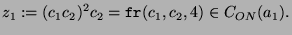 |
(4.5) |
Dann ist
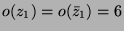 . Nach [CCN$^$85,
. Nach [CCN$^$85, 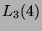 ,
Seite 23] ist bekannt, daß
,
Seite 23] ist bekannt, daß
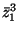 in der Klasse
2B von
in der Klasse
2B von
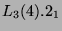 liegt. Suche also in
liegt. Suche also in
 nach Elementen der Ordnung 3:
nach Elementen der Ordnung 3:
- Es ist klar, daß
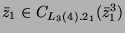 und
es gilt
und
es gilt
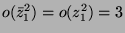 .
.
- Da
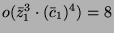 , definiere
, definiere
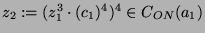 , so ist
, so ist
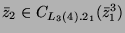 .
.
- Da
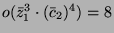 , definiere
, definiere
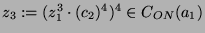 , so ist
, so ist
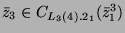 .
.
- Es gilt
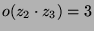 .
.
Damit folgt
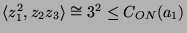 . Mit GAP kann man nachrechnen, daß
. Mit GAP kann man nachrechnen, daß
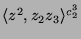 die oben gefundene Gruppe
die oben gefundene Gruppe
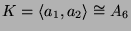 aus (4.4) zentralisiert. Definiere
also
aus (4.4) zentralisiert. Definiere
also
so ist
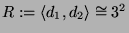 und es gilt nach
Konstruktion
und es gilt nach
Konstruktion
Das folgende Script berechnet d.1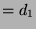 und d.2
und d.2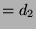 mit der MeatAxe:
mit der MeatAxe:






Next: Bestimme
Up: Die sechste maximale Untergruppe
Previous: Bestimme
Inhalt
Index
Markus Ottensmann
2000-02-10
![]() , die von
, die von
![]() zentralisiert wird. Nach (4.2) gilt dann
zentralisiert wird. Nach (4.2) gilt dann
![]() .
.
![]() , Seite 23] gilt
, Seite 23] gilt
![]() und
und
![]() , also folgt
, also folgt
![]() . Suche also ein 2B-Element in
. Suche also ein 2B-Element in
![]() und suche im Zentralisator
und suche im Zentralisator
![]() Elemente der Ordnung 3.
Elemente der Ordnung 3.
![]() hat neun Bahnen auf den Punkten
hat neun Bahnen auf den Punkten
![]() . Sei
. Sei ![]() die Bahn der Länge 120. Dann ist
die Bahn der Länge 120. Dann ist
![]() . Sei
. Sei
![]() die Einschränkung auf die Bahn
die Einschränkung auf die Bahn ![]() . Dann gilt
. Dann gilt
![]() . Sei
. Sei
![]() und d.2
und d.2![]() mit der MeatAxe:
mit der MeatAxe:
