Bestimme $A_6\leq C_{ON}(a)$

Für $R \cong \texttt{3A}^2\leq ON$ ist nach [O'N96, Lemma 5.3 und Lemma 5.5, Seite 447]

$$C_{ON}(R) \cong R\times K, K\cong L_2(9)\cong A_6.$$ (4.2)

Das nächste Ziel ist also, eine Untergruppe $K\cong A_6$ zu finden.

Sei $C_{ON}(a) = \langle x_1,x_2\rangle$. Dann hat $C_{ON}(a)$ neun Bahnen auf den Punkten $\{1,\dots,122\,760\}$. Wird die Operation von $C_{ON}(a)$ auf die Bahn mit der Länge von 120 Punkten eingeschränkt, so erhält man eine Gruppe, die isomorph zu $L_3(4).2$ ist.

Mit MeatAxe wird das Erzeugnis von x.1$=x_1$, x.2$=x_2$ auf die Bahn der Länge 120 eingeschränkt, indem sukzessive die Operation auf einer Bahn (s- $i$.) und dem Rest (q- $i$.) ausgerechnet wird:

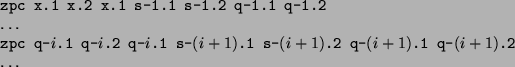
bis durch s- $i$.1, s- $i$.2 eine Operation auf 120 Punkten beschrieben wird. Bezeichne mit $\bar{x}$ das auf die Bahn der Länge 120 eingeschränkte Element $x\in ON$. Seien $s_1 := \bar{x}_1$ und $s_2 := \bar{x}_2$. Dann kann man nachrechnen, daß $o(x_1x_2) = o(s_1s_2) = 8$. Betrachte die Elemente $z_1,z_2 \in C_{ON}(x)$ als Worte in den Erzeugern $x_1,x_2$:

$$\begin{split}z_1 &:= x_1 x_2 = \texttt{fr}(x_1,x_2,3) \quad\t... ...= \texttt{fr}(x_1,x_2,5) \quad\text{mit }o(z_2)=28. \end{split}$$ (4.3)

• Anhand der Charaktertafel von $4_2.L_3(4).2_1$ sieht man, daß $(s_1s_2)^2 \in \texttt{4A} \subset L_3(4).2_1$ (in der Charaktertafel von $L_3(4).2_1$ in GAP ist dies die Klasse 4). Anhand der zweiten Potenzabbildung ebendieser Charaktertafel sieht man desweiteren, daß $z_1^2 \in \texttt{4A} \subset 4_2.L_3(4).2_1$ ist (in der Charaktertafel in GAP ist dies die Klasse 9).
• Es gilt $o(x_2)=16$. Anhand der Potenzabbildung sieht man, daß $s_2^4 \in \texttt{2A}\subset L_3(4).2_1$.
• Es gilt $\bar{z}_2^7 = ((s_1s_2)^3s_2)^7 \in \texttt{1A}\subset L_3(4).2_1$.
• Damit folgt, daß $y_1 := x_2^4 z_2^7$ in einem Urbild der Klasse 2A von $L_3(4).2_1$ liegt. Da $o(y_1) = 2$ folgt, daß $y_1 \in \texttt{2A}\subset 4_2.L_3(4).2_1$ ist.

Definiere $x := y_1\in \texttt{2A}\subset 4_2.L_3(4).2_1$ und $y := z_1^2\in \texttt{4A}\subset 4_2.L_3(4).2_1$. Mit randomisiertem Konjugieren in GAP von $y$ mit den Elementen

$$g_1 := (x_1x_2)^5x_2 = \texttt{fr}(x_1,x_2,8), o(g_1)=28$$

$$g_2 := (x_1x_2)^2x_2(x_1x_2)^3x_2x_1x_2^2 = \texttt{fr}(x_1,x_2,9), o(g_2)=16,$$

wird ein $g\in \langle g_1,g_2\rangle$ gesucht, so daß $x\cdot y^g$ ein Element der Ordnung 5 ist. Dazu benutze das GAP-Programm aus Abbildung 4.1.

Abbildung 4.1: Randomsuche in GAP

Die Berechnung mit GAP ergibt, daß $o(x\cdot y^g) = 5$ für $g = g_2^6 g_1^2 g_2 g_1^2 g_2^4$ und $\langle x,y^g\rangle$ ist eine Gruppe von Ordnung 720 mit (nichttrivialen) Normalteilern der Ordnung 2 und 360.

$z_2^{14}$ ist ein Element der Ordnung 2 das zentral in $C_{ON}(x)$ liegt. In GAP läßt sich nun nachrechnen, daß $z_2^{14}\in \langle x,y^g\rangle$ und für $a_1 := z_2^{14}x$ und $a_2 := z_2^{14} y^g$ ist $\langle a_1,a_2\rangle$ eine einfache Gruppe der Ordnung 360. Also ist

$$K := \langle a_1, a_2\rangle \cong A_6.$$ (4.4)

Nun ist $a_1 = (x_2^4)((x_1x_2)^3x_2)^{21} \in \texttt{2A}\subset 4_2.L_3(4).2_1$.

Das folgende Script berechnet a.1$= a_1$ und a.2$= a_2$ mit der MeatAxe: