




Next: Bestimme
Up: Die sechste maximale Untergruppe
Previous: Bestimme
Inhalt
Index
Bestimme nun wie oben Erzeuger für
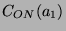 . Dazu betrachte die
Standarderzeuger
. Dazu betrachte die
Standarderzeuger 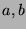 von
von 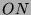 und das Element
und das Element
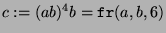 mit
mit 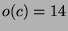 .
.
- Da
 , wird
, wird 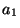 von
von 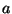 zentralisiert.
zentralisiert.
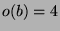 und
und
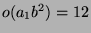 , also ist
, also ist
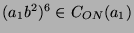 .
.
- Da
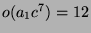 , ist auch
, ist auch
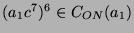 .
.
Seien
dann folgt
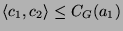 . In GAP läßt sich
berechnen, daß
. In GAP läßt sich
berechnen, daß
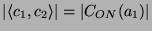 . Also gilt
. Also gilt
Das folgende Script berechnet c.1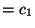 und c.2
und c.2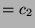 mit der MeatAxe:
mit der MeatAxe:

Markus Ottensmann
2000-02-10
![]() . Dazu betrachte die
Standarderzeuger
. Dazu betrachte die
Standarderzeuger ![]() von
von ![]() und das Element
und das Element
![]() mit
mit ![]() .
.
![]() und c.2
und c.2![]() mit der MeatAxe:
mit der MeatAxe:
