




Next: Permutationsdarstellung von auf 368820
Up: Konstruktionen
Previous:
Inhalt
Index
Der Permutationsmodul
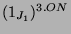
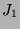 ist eine maximale Untergruppe von
ist eine maximale Untergruppe von  mit Ordnung
mit Ordnung
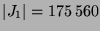 und Index
und Index
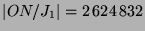 . Der
Schurmultiplikator von
. Der
Schurmultiplikator von 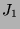 ist 1. Daher ist das Urbild von
ist 1. Daher ist das Urbild von 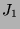 in
in
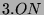 isomorph zu
isomorph zu
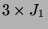 .
.
In [JW94, Abschnitt 6.G] wird eine Konstruktion der
Permutationsdarstellung
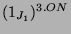 von
von 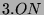 auf
den Nebenklassen von
auf
den Nebenklassen von 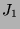 wie folgt angegeben.
wie folgt angegeben.
Seien  und
und  Standarderzeuger für
Standarderzeuger für 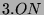 . Dann ist
. Dann ist
Bezeichne mit
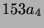 eine der beiden 153-dimensionalen
Moduln von
eine der beiden 153-dimensionalen
Moduln von 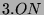 über
über 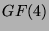 . Wird
. Wird 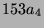 auf die Operation von
auf die Operation von
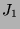 eingeschränkt, so folgt mit dem MeatAxe-Programm
chop
Hieraus läßt sich einfach ein Fixvektor für
eingeschränkt, so folgt mit dem MeatAxe-Programm
chop
Hieraus läßt sich einfach ein Fixvektor für 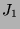 bestimmen. Dazu
berechnet man die Nullräume von
bestimmen. Dazu
berechnet man die Nullräume von
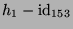 , bzw.
, bzw.
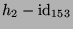 . Der Schnitt dieser beiden Nullräume ist
eindimensional und liefert somit einen Fixvektor
. Der Schnitt dieser beiden Nullräume ist
eindimensional und liefert somit einen Fixvektor 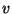 Durch Permutation von
Durch Permutation von 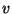 mit
mit  und
und  erhält man eine
Permutationsdarstellung von
erhält man eine
Permutationsdarstellung von  auf den Nebenklassen von
auf den Nebenklassen von 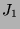 ,
also auf
,
also auf
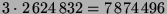 Punkten (Um dies zu
berechnen hat helios (ein Pentium II 400MHz PC am Lehrstuhl D
für Mathematik) eine Stunde gerechnet und etwa 480MB Speicher
benutzt).
Punkten (Um dies zu
berechnen hat helios (ein Pentium II 400MHz PC am Lehrstuhl D
für Mathematik) eine Stunde gerechnet und etwa 480MB Speicher
benutzt).
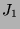 ist der Einpunkt-Stabilisator der 1, d.h.
ist der Einpunkt-Stabilisator der 1, d.h.
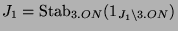 . Da
. Da
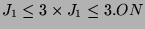 gibt es ein Blocksystem
gibt es ein Blocksystem
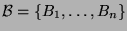 mit
mit
 . Sei
. Sei 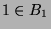 und
und 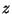 das zentrale
Element der Ordnung 3, dann ist
das zentrale
Element der Ordnung 3, dann ist
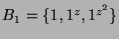 . Die
Permutation der Blöcke liefert nun Permutationen von
. Die
Permutation der Blöcke liefert nun Permutationen von 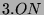 auf den
Restklassen nach
auf den
Restklassen nach
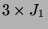 und damit eine Permutationsdarstellung
von
und damit eine Permutationsdarstellung
von  auf den Restklassen nach
auf den Restklassen nach 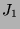 .
=-38mm
=17
.
=-38mm
=17
![$\textstyle \parbox{0mm}{\hspace*{0.5em}
\setlength{\unitlength}{1mm}
\begin{pi...
...}}
\put(24,27){\circle{1}}
\put(25,27){\makebox(0,0)[l]{$ON$}}
\end{picture}}$](img1510.png)





Next: Permutationsdarstellung von auf 368820
Up: Konstruktionen
Previous:
Inhalt
Index
Markus Ottensmann
2000-02-10
![]() ist eine maximale Untergruppe von
ist eine maximale Untergruppe von ![]() mit Ordnung
mit Ordnung
![]() und Index
und Index
![]() . Der
Schurmultiplikator von
. Der
Schurmultiplikator von ![]() ist 1. Daher ist das Urbild von
ist 1. Daher ist das Urbild von ![]() in
in
![]() isomorph zu
isomorph zu
![]() .
.
![]() von
von ![]() auf
den Nebenklassen von
auf
den Nebenklassen von ![]() wie folgt angegeben.
wie folgt angegeben.
![]() und
und ![]() Standarderzeuger für
Standarderzeuger für ![]() . Dann ist
. Dann ist
![$\textstyle \parbox{0mm}{\hspace*{0.5em}
\setlength{\unitlength}{1mm}
\begin{pi...
...}}
\put(24,27){\circle{1}}
\put(25,27){\makebox(0,0)[l]{$ON$}}
\end{picture}}$](img1510.png)