




Next: Rekonstruktionen der Brauerbäume
Up: Einleitung
Previous: Defekte
Inhalt
Index
Die Brauerbäume
1.2.1 Definition
Seien

zwei primitive Idempotente.
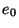
und
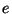
heißen
verbunden, wenn es eine Menge von primitiven Idempotenten

gibt, so daß
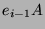
und
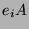
für jedes
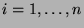
einen gemeinsamen Kompositionsfaktor haben.
1.2.2 Satz
Seien
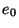
und
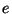
zwei primitive Idempotente. Dann sind
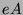
und
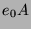
genau dann verbunden, wenn sie in einem Block liegen.
Beweis:Siehe z.B.[Fei82, Theorem I,13.11, Seite 45].
1.2.3 Definition
Sei
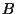
ein Block der Gruppe
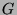
mit positivem Defekt. Der
Brauer-Graph
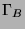
von
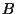
ist wie folgt definiert:
Es gibt eine Bijektion zwischen der Menge der auf
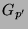
eingeschränkten irreduziblen gewöhnlichen Charaktere
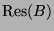
und
den Knoten von
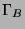
. Zwei Knoten sind durch eine Kante
verbunden, wenn sie verschieden sind und wenn es einen
irreduziblen Brauercharakter

gibt, der
gemeinsamer Konstituent der eingeschränkten gewöhnlichen
Charaktere
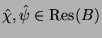
ist,
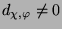
und
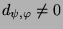
gilt.
Eine Folgerung aus dem nächsten Satz ist, daß eine Bijektion
zwischen den Kanten des Brauer-Graphen und den irreduziblen
Brauercharakteren existiert. Der Satz wurde ursprünglich von Brauer
(1941) für Blöcke von Defekt 1 gezeigt und von Dade (1966) erweitert
für Blöcke mit beliebigem zyklischen Defekt - siehe [HL89, Theorem
2.1.5, Seite 13f].
1.2.4 Satz
Es sei
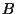
ein Block mit zyklischer Defektgruppe von Ordnung
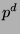
. Dann existieren

irreduzible Brauercharaktere

in
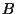
. Die Anzahl der gewöhnlichen
irreduziblen Charaktere in
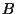
ist
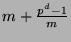
. Diese
Charaktere werden mit
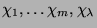
, mit
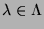
bezeichnet, wobei
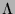
eine Indexmenge mit
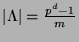
ist. Die
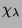
, für
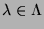
, werden
exzeptionelle Charaktere in
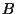
genannt. Diese schränken auf den
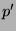
-Klassen gleich
ein. Definiere
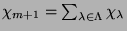
und schreibe
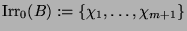
.
Sei 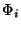 der gewöhnliche Charakter des projektiven
unzerlegbaren Moduls
der gewöhnliche Charakter des projektiven
unzerlegbaren Moduls 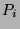 , der zum Brauercharakter
, der zum Brauercharakter 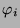 gehört. Dann existieren
gehört. Dann existieren
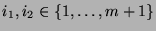 ,
,
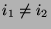 , so daß
, so daß
Beweis:Siehe z.B.[Fei82, Theorem VII,2.12 und Theorem VII,2.15, Seite
277f].
Mit diesem Satz folgt, daß jeder Brauercharakter 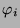 für
für
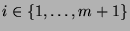 ein irreduzibler Konstituent nur von
ein irreduzibler Konstituent nur von
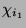 und
und
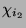 (mit Vielfachheit 1) ist. Ist
(mit Vielfachheit 1) ist. Ist 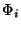 ein
projektiver unzerlegbarer Charakter in Block
ein
projektiver unzerlegbarer Charakter in Block 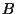 , so folgt mit der
Brauerreziprozität, daß
, so folgt mit der
Brauerreziprozität, daß
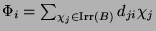 gilt (siehe auch [CR62, Theorem (83.9), Seite
593]). Somit folgt, daß
gilt (siehe auch [CR62, Theorem (83.9), Seite
593]). Somit folgt, daß
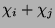 genau dann
projektiv ist, wenn
genau dann
projektiv ist, wenn
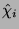 und
und
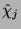 einen
gemeinsamen Brauercharakter als Konstituenten haben.
einen
gemeinsamen Brauercharakter als Konstituenten haben.
Eine Folgerung aus dem Satz 1.2.4 ist der folgende
Satz.
1.2.5 Satz
Ist
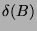
zyklische Defektgruppe, so ist der Brauer-Graph von
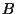
ein Baum, Graph enthält keine Kreise. Dann wird der
Brauer-Graph auch
Brauerbaum genannt.
Beweis:Siehe z.B.[Fei82, Lemma VII,6.4, Seite 300].
1.2.6 Bemerkung
Es gilt
Also sieht man direkt, daß in Charakteristik
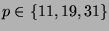
die
Defektgruppen eines Blockes mit positivem Defekt von
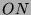
bzw.
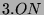
zyklisch von Ordnung
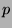
sind.





Next: Rekonstruktionen der Brauerbäume
Up: Einleitung
Previous: Defekte
Inhalt
Index
Markus Ottensmann
2000-02-10
![]() der gewöhnliche Charakter des projektiven
unzerlegbaren Moduls
der gewöhnliche Charakter des projektiven
unzerlegbaren Moduls ![]() , der zum Brauercharakter
, der zum Brauercharakter ![]() gehört. Dann existieren
gehört. Dann existieren
![]() ,
,
![]() , so daß
, so daß
![]() für
für
![]() ein irreduzibler Konstituent nur von
ein irreduzibler Konstituent nur von
![]() und
und
![]() (mit Vielfachheit 1) ist. Ist
(mit Vielfachheit 1) ist. Ist ![]() ein
projektiver unzerlegbarer Charakter in Block
ein
projektiver unzerlegbarer Charakter in Block ![]() , so folgt mit der
Brauerreziprozität, daß
, so folgt mit der
Brauerreziprozität, daß
![]() gilt (siehe auch [CR62, Theorem (83.9), Seite
593]). Somit folgt, daß
gilt (siehe auch [CR62, Theorem (83.9), Seite
593]). Somit folgt, daß
![]() genau dann
projektiv ist, wenn
genau dann
projektiv ist, wenn
![]() und
und
![]() einen
gemeinsamen Brauercharakter als Konstituenten haben.
einen
gemeinsamen Brauercharakter als Konstituenten haben.