




Next: Die Brauerbäume
Up: Grundlegende Definitionen und Bemerkungen
Previous: Blöcke
Inhalt
Index
Sei 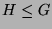 und
und 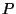 ein
ein 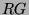 -Modul.
-Modul. 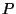 heißt
heißt
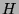 -projektiv, falls
-projektiv, falls
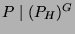 .
.
1.1.10 Lemma
Sei

ein diskreter Bewertungsring und
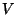
ein unzerlegbarer
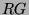
-Modul. Dann existiert eine bis auf Konjugation eindeutige
minimale
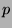
-Untergruppe
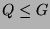
, so daß
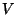
ein
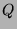
-projektiver
Modul ist.
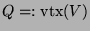
heißt
Vertex von
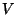
.
Beweis:Siehe z.B.[Fei82, Corollary III,4.3 und Lemma III,4.4, Seite
112f].
Betrachte 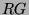 als
als
![$ R[G\times G]$](img248.png) -Modul mit
-Modul mit
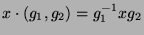 für
für
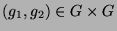 und
und 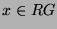 . Dann ist
. Dann ist
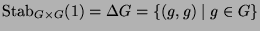 . Also ist
. Also ist
für die zentral-primitiven Idempotente 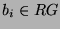 (siehe z.B.
[Fei82, Lemma III,8.2, Seite 132]). Die direkten Summanden
(siehe z.B.
[Fei82, Lemma III,8.2, Seite 132]). Die direkten Summanden 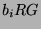 des
des
![$ R[G\times G]$](img248.png) -Moduls
-Moduls 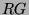 sind die zweiseitige Ideale von
sind die zweiseitige Ideale von
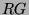 . Da
. Da
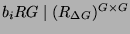 ist
ist
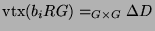 für ein
für ein 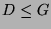 . Dieses
. Dieses
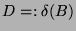 heißt
Defektgruppe des Blocks
heißt
Defektgruppe des Blocks 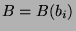 . Nach Lemma
1.1.10 ist
. Nach Lemma
1.1.10 ist 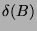 eine
eine 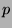 -Gruppe, also ist
-Gruppe, also ist
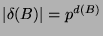 für ein
für ein
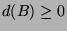 .
.
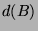 heißt Defekt von
heißt Defekt von 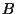 (siehe z.B.[Fei82, III,6, Seite 126]).
(siehe z.B.[Fei82, III,6, Seite 126]).
Beweis:Siehe [Fei82, Lemma IV,4.19, Seite 159].





Next: Die Brauerbäume
Up: Grundlegende Definitionen und Bemerkungen
Previous: Blöcke
Inhalt
Index
Markus Ottensmann
2000-02-10
![]() und
und ![]() ein
ein ![]() -Modul.
-Modul. ![]() heißt
heißt
![]() -projektiv, falls
-projektiv, falls
![]() .
.
![]() als
als
![]() -Modul mit
-Modul mit
![]() für
für
![]() und
und ![]() . Dann ist
. Dann ist
![]() . Also ist
. Also ist