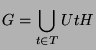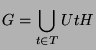Induzierte Moduln

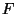
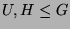
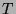
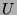
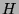
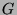
2.2.2 Satz (Mackey)   75 Sei $F$ ein Körper, seien $U,H\leq G$ und sei $T$ Vertretersystem der $U$-$H$-Doppelnebenklassen von $G$, d.h.

$$G = \bigcup_{t\in T} U t H$$

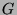
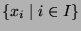
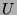
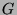
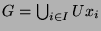
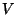
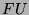
ist eine disjunkte Vereinigung von $G$. Sei $\{x_i\mid i\in I\}$ ein Vertretersystem der Rechtsnebenklassen von $U$ in $G$, d.h. $G = \bigcup_{i\in I} U x_i$. Sei $V$ ein $FU$-Modul. Dann gilt

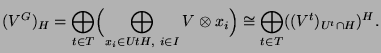$$(V^G\glossary{$V^G$>induzierter Modul})_H = \bigoplus_{t\in T} \B... ...H,\ i\in I} V\otimes x_i \Bigr) \cong \bigoplus_{t\in T} ((V^t)_{U^t\cap H})^H.$$ (2.6)

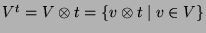
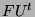
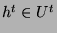
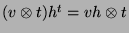
Dabei ist $V^t = V\otimes t = \{v\otimes t\mid v\in V\}$ ein $FU^t$-Modul, wobei die Operation von $h^t\in U^t$ auf $v\otimes t$ definiert ist durch $(v\otimes t)h^t = vh\otimes t$.

Beweis:Siehe [Fei82, Theorem II,2.9, Seite 85].