Sei ![]() und
und
![]() ein
ein ![]() -dimensionaler
-dimensionaler
![]() -Permutationsmodul mit
-Permutationsmodul mit ![]() -Basis
-Basis
![]() .
. ![]() operiert auf
operiert auf ![]() durch Permutation der Basisvektoren
durch Permutation der Basisvektoren
![]() für
für
![]() . Sei
. Sei ![]() mit
mit
![]() Kondensationsgruppe und
Kondensationsgruppe und ![]() das zu
das zu ![]() gehörige zentrale
Idempotent. Seien
gehörige zentrale
Idempotent. Seien
![]() die Bahnen von
die Bahnen von
![]() unter
unter ![]() , dann existiert zu jedem
, dann existiert zu jedem ![]() ein
ein ![]() mit
mit
![]() . Dadurch wird eine Abbildung
. Dadurch wird eine Abbildung ![]() definiert:
definiert:
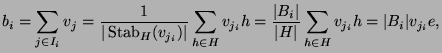 für
für
![[*]](cross_ref_motif.png) .
.
Sei ![]() die dreifache Überlagerung der O'Nan-Gruppe.
die dreifache Überlagerung der O'Nan-Gruppe.
![]() und
und
![]() seien Standarderzeuger von
seien Standarderzeuger von
![]() als Permutationen auf den Nebenklassen von
als Permutationen auf den Nebenklassen von ![]() nach
nach ![]() ,
also auf
,
also auf
![]() Punkten gegeben. Die
Konstruktion dieser Permutationen wird in Abschnitt
4.4 beschrieben. Wie in Abschnitt
4.2 beschrieben, werden die Erzeuger
Punkten gegeben. Die
Konstruktion dieser Permutationen wird in Abschnitt
4.4 beschrieben. Wie in Abschnitt
4.2 beschrieben, werden die Erzeuger
![]() und
und
![]() der Untergruppe
der Untergruppe
![]() aus den
Standarderzeugern
aus den
Standarderzeugern ![]() berechnet. Sei
berechnet. Sei ![]() nach
(2.1).
nach
(2.1).
Um den kondensierten Modul ![]() mit der MeatAxe zu berechnen muß
man folgendes machen:
mit der MeatAxe zu berechnen muß
man folgendes machen:
Zunächst bestimmt man mit dem MeatAxe-Programm
zmo die Bahnen ![]() der Operation
der Untergruppe
der Operation
der Untergruppe
![]() . Dazu
werden als Parameter die Untergruppenerzeuger (k) und die
Ausgabedateien, in die die Bahnen (orb) und die
Bahnenlängen (szg) geschrieben werden, übergeben:
. Dazu
werden als Parameter die Untergruppenerzeuger (k) und die
Ausgabedateien, in die die Bahnen (orb) und die
Bahnenlängen (szg) geschrieben werden, übergeben:
![]()
orb enthält nun die Bahnen ![]() als Vektor aller
Punkte. In szg sind die Längen der Bahnen enthalten. Ist
als Vektor aller
Punkte. In szg sind die Längen der Bahnen enthalten. Ist
![]() die erste Zahl aus szg (Länge der
ersten Bahn), so gehören die ersten
die erste Zahl aus szg (Länge der
ersten Bahn), so gehören die ersten ![]() Punkte aus orb
zu
Punkte aus orb
zu ![]() . Ist
. Ist
![]() die zweite Zahl aus szg, so
gehören die Punkte von
die zweite Zahl aus szg, so
gehören die Punkte von ![]() bis
bis ![]() aus orb zu
aus orb zu
![]() , etc.
, etc.
Das MeatAxe-Programm zkd, das für ein
Element ![]() eine Darstellung der Operation von
eine Darstellung der Operation von ![]() nach
(2.5) berechnet, geht oBdA.davon aus, daß die Bahnen
nach
(2.5) berechnet, geht oBdA.davon aus, daß die Bahnen
![]() unter der Operation von
unter der Operation von ![]() konsekutiv sind,
d.h.
konsekutiv sind,
d.h.
![]() ,
,
![]() , etc.
Mit der MeatAxe erreicht man dies, indem alle Gruppenelemente mit
dem Bahnvektor orb ,,konjugiert`` werden.
, etc.
Mit der MeatAxe erreicht man dies, indem alle Gruppenelemente mit
dem Bahnvektor orb ,,konjugiert`` werden.

Das Ergebnis der Kondensation ist in kdg.1 enthalten, d.h.
![]() . Die letzten drei Befehle
werden auch auf den Gruppenerzeuger
. Die letzten drei Befehle
werden auch auf den Gruppenerzeuger ![]() angewendet, sowie auf alle
weiteren Elementen
angewendet, sowie auf alle
weiteren Elementen ![]() , die kondensiert werden sollen. Nach der
Untersuchung in Abschnitt 3.4 ist bekannt, daß
, die kondensiert werden sollen. Nach der
Untersuchung in Abschnitt 3.4 ist bekannt, daß
![]() . Die
. Die
![]() -Matrizen kdg.
-Matrizen kdg.![]() geben nun die Operation der kondensierten Elemente
geben nun die Operation der kondensierten Elemente ![]() auf
auf ![]() an.
an.
![]()