Sei ![]() ein Körper und seien
ein Körper und seien ![]() , so daß
, so daß
![]() . Sei
. Sei ![]() ein
ein ![]() -Modul und
-Modul und ![]() das zu
das zu ![]() gehörige
Idempotent nach (2.1). Sei
gehörige
Idempotent nach (2.1). Sei
![]() für eine
geeignete Indexmenge
für eine
geeignete Indexmenge ![]() ein Vertretersystem der
ein Vertretersystem der
![]() -
-![]() -Doppelnebenklassen in
-Doppelnebenklassen in ![]() , d.h.
, d.h.
![]() . Für alle
. Für alle ![]() sei
sei
![]() für
eine geeignete Indexmenge
für
eine geeignete Indexmenge ![]() ein Vertretersystem der
ein Vertretersystem der
![]() -Rechtsnebenklassen in
-Rechtsnebenklassen in ![]() , ür alle
, ür alle ![]() gilt
gilt
![]() . Dann gilt
. Dann gilt
 |
||
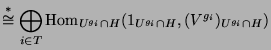 |
||
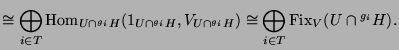 |
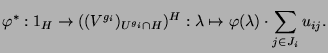
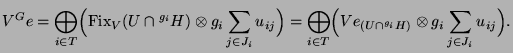
Die Operation von
![]() für ein
für ein ![]() auf
auf ![]() kann nun
durch die Operation von
kann nun
durch die Operation von ![]() und
und ![]() auf
auf ![]() in der Mackey-Zerlegung
bestimmt werden. Für
in der Mackey-Zerlegung
bestimmt werden. Für ![]() existieren
existieren ![]() ,
, ![]() und
und
![]() (abhängig von
(abhängig von ![]() und
und ![]() ) so daß
) so daß

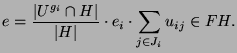
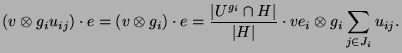
Die Implementierung dieser Berechnungen in GAP wird in [MR99] beschrieben. Für die Berechnungen wird eine Implementation von GAP mit der MeatAxe-Arithmetik für endliche Körper verwendet [Kim97].
![[*]](cross_ref_motif.png) .
.
![]() und
und ![]() seien Standarderzeuger von
seien Standarderzeuger von ![]() , die als Permutationen
auf 368
, die als Permutationen
auf 368![]() 280 Punkten gegeben sind. Die Konstruktion dieser
Permutationsdarstellung wird in Abschnitt
4.5 beschrieben. Wie in Abschnitt
4.2 beschrieben, werden die Erzeuger
280 Punkten gegeben sind. Die Konstruktion dieser
Permutationsdarstellung wird in Abschnitt
4.5 beschrieben. Wie in Abschnitt
4.2 beschrieben, werden die Erzeuger
![]() und
und
![]() der Untergruppe
der Untergruppe
![]() aus den
Standarderzeugern
aus den
Standarderzeugern ![]() berechnet. Die Ordnung von
berechnet. Die Ordnung von ![]() ist
14
ist
14![]() 880.
880.
![\begin{alltt}
gap> gens := [a,b];; ...](img506.png)
Die ![]() -
-![]() -Doppelnebenklassen in
-Doppelnebenklassen in ![]() stehen in Bijektion mit den
stehen in Bijektion mit den
![]() -Bahnen auf
-Bahnen auf ![]() . Eine geeignete Menge
. Eine geeignete Menge
![]() wird durch einen randomisierten Schreier-Sims-Algorithmus
gefunden. Da
wird durch einen randomisierten Schreier-Sims-Algorithmus
gefunden. Da
![]() , erhält man auch ein
Erzeugendensystem für
, erhält man auch ein
Erzeugendensystem für ![]() . Ebenso erhält man für
. Ebenso erhält man für
![]() eine geeignete Menge
eine geeignete Menge
![]() durch den Schreier-Sims-Algorithmus. Dies berechnet die Methode
InitIndCond().
durch den Schreier-Sims-Algorithmus. Dies berechnet die Methode
InitIndCond().
![]()
infoperm.chain ist die mit dem Schreier-Sims-Algorithmus
gefundene Stabilisatorkette. Die Methode StabGens()
bestimmt die Liste sgens der Erzeuger des ersten
Stabilisators in der Stabilisatorkette. Der erste Stabilisator ist
![]() . Aus diesen Erzeugern
erhält man folgendermaßen eine Permutationsdarstellung von
. Aus diesen Erzeugern
erhält man folgendermaßen eine Permutationsdarstellung von
![]() auf 456 Punkten:
auf 456 Punkten:
![]()
Nun wird die Operation von ![]() auf die Bahn der Länge 19
auf die Bahn der Länge 19![]() 152
eingeschränkt. Dann werden nacheinander minimale Blocksysteme
berechnet und die Operation wird auf diese Blocksysteme eingeschränkt.
152
eingeschränkt. Dann werden nacheinander minimale Blocksysteme
berechnet und die Operation wird auf diese Blocksysteme eingeschränkt.
![\begin{alltt}
gap> So := Operation(S, orbs[5]);; ...](img512.png)
Die Erzeuger von
![]() sind nun als
Permutationen auf 456 Punkten gegeben. Nun kann, wie in Abschnitt
4.8 beschrieben, ein 56-dimensionaler Modul
über
sind nun als
Permutationen auf 456 Punkten gegeben. Nun kann, wie in Abschnitt
4.8 beschrieben, ein 56-dimensionaler Modul
über ![]() konstruiert werden. Sei rep die Liste der
aus sgens bestimmten Erzeuger des 56-dimensionalen
konstruiert werden. Sei rep die Liste der
aus sgens bestimmten Erzeuger des 56-dimensionalen
![]() -Moduls
-Moduls ![]() . Nun werden in einem ersten Schritt die Berechnungen
für
. Nun werden in einem ersten Schritt die Berechnungen
für ![]() durchgeführt, die nur einmal für alle zu kondensierenden
Elemente
durchgeführt, die nur einmal für alle zu kondensierenden
Elemente ![]() gemacht werden müssen (für eine genauere
Beschreibung dieser Schritte siehe [MR99, Abschnitt
4.2]):
gemacht werden müssen (für eine genauere
Beschreibung dieser Schritte siehe [MR99, Abschnitt
4.2]):
![]()
Schließlich können nacheinander alle gewünschten Elemente ![]() kondensiert werden:
kondensiert werden:
![]()
cond enthält nun (entsprechend der Analyse in Abschnitt
3.2) eine 1![]() 482-dimensionale Matrix über
482-dimensionale Matrix über
![]() , die bis auf einen Faktor
, die bis auf einen Faktor
![]() der Darstellung
von
der Darstellung
von ![]() entspricht. Damit gilt
entspricht. Damit gilt
![]() .
.
![]()