




Next: Konstruktionen
Up: Primzahl 31, Block 2
Previous: Der Brauerbaum
Inhalt
Index
Für den Beweis wird der Permutationsmodul
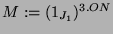 mit der Kondensationsgruppe
mit der Kondensationsgruppe
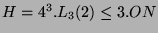 kondensiert. In der Tabelle
3.43 sind die Zerlegungszahlen des zweiten Blocks
für die Permutationsmoduln und in der Tabelle 3.44
sind die Dimensionen der einfachen kondensierten Moduln des zweiten
Blocks zu sehen. Die Dimension des kondensierten Permutationsmoduls
ist 877. Die Kondensationsalgebra ist
kondensiert. In der Tabelle
3.43 sind die Zerlegungszahlen des zweiten Blocks
für die Permutationsmoduln und in der Tabelle 3.44
sind die Dimensionen der einfachen kondensierten Moduln des zweiten
Blocks zu sehen. Die Dimension des kondensierten Permutationsmoduls
ist 877. Die Kondensationsalgebra ist
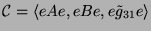 .
.
Tabelle 3.43:
Zerlegungszahlen (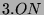 , Primzahl 31, Block 2)
, Primzahl 31, Block 2)
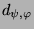 |
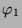 |
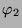 |
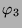 |
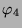 |
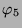 |
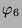 |
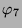 |
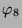 |
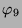 |
 |
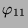 |
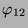 |
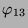 |
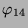 |
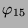 |
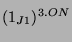 |
2 |
2 |
2 |
2 |
2 |
2 |
0 |
4 |
3 |
4 |
1 |
3 |
3 |
3 |
1 |
|
Tabelle 3.44:
Skalarprodukte ( , Primzahl 31, Block 2)
, Primzahl 31, Block 2)
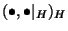 |
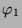 |
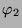 |
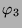 |
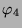 |
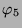 |
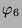 |
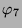 |
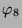 |
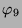 |
 |
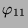 |
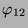 |
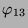 |
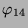 |
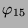 |
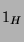 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
15 |
8 |
4 |
8 |
11 |
15 |
4 |
|
Beim Kondensieren des Permutationsmoduls ergeben sich für das
kondensierte Element
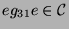 die Spuren auf den
Konstituenten von
die Spuren auf den
Konstituenten von
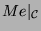 entsprechend der Tabelle
3.45. In der Tabelle 3.46
sind die Werte
entsprechend der Tabelle
3.45. In der Tabelle 3.46
sind die Werte
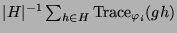 der
Spurformel (2.3) für das Element
der
Spurformel (2.3) für das Element
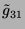 enthalten.
enthalten.
Tabelle 3.45:
Spuren des kondensierten Elements
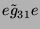 auf den Konstituenten von
auf den Konstituenten von
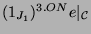 ,
(
,
(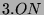 , Primzahl 31, Block 2).
, Primzahl 31, Block 2).
| Name |
Anzahl |
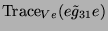 |
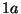 |
3 |
 |
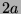 |
3 |
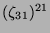 |
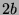 |
3 |
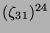 |
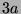 |
1 |
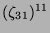 |
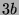 |
1 |
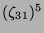 |
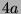 |
1 |
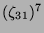 |
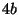 |
4 |
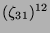 |
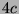 |
1 |
0 |
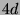 |
1 |
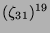 |
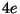 |
1 |
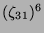 |
 |
4 |
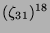 |
 |
1 |
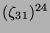 |
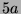 |
1 |
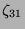 |
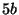 |
1 |
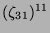 |
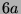 |
3 |
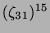 |
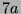 |
1 |
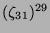 |
 |
1 |
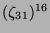 |
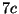 |
1 |
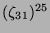 |
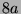 |
4 |
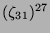 |
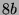 |
3 |
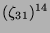 |
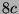 |
1 |
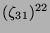 |
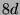 |
3 |
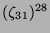 |
 |
1 |
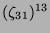 |
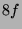 |
4 |
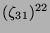 |
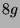 |
3 |
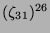 |
| 720 |
|
|
| Name |
Anzahl |
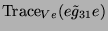 |
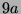 |
3 |
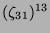 |
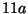 |
3 |
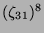 |
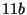 |
3 |
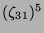 |
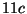 |
3 |
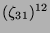 |
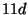 |
1 |
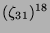 |
 |
1 |
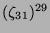 |
 |
2 |
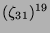 |
 |
2 |
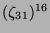 |
 |
2 |
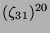 |
 |
2 |
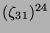 |
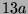 |
1 |
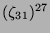 |
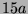 |
3 |
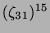 |
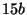 |
3 |
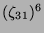 |
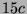 |
3 |
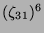 |
 |
3 |
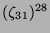 |
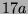 |
3 |
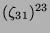 |
 |
2 |
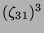 |
 |
2 |
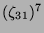 |
 |
2 |
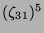 |
| 740 |
|
|
|
Vergleiche nun die verschiedenen, für die einzelnen Fälle
berechneten, Spuren nach der Spurformel (2.3) für das
Element
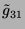 :
:
- Nach der Tabelle 3.44 kondensiert
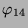 zu einem Modul der Dimension 15, der nach Tabelle
3.43 in
zu einem Modul der Dimension 15, der nach Tabelle
3.43 in
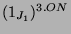 mit Vielfachheit drei
vorkommt. Mit der Tabelle 3.45 folgt nun, daß
mit Vielfachheit drei
vorkommt. Mit der Tabelle 3.45 folgt nun, daß
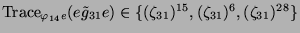 . Dies ist nur bei vier
verschiedenen Kandidaten der Fall.
. Dies ist nur bei vier
verschiedenen Kandidaten der Fall.
-
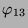 kondensiert zu einem Modul der Dimension elf, der
in
kondensiert zu einem Modul der Dimension elf, der
in
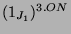 mit Vielfachheit drei vorkommt. Also gilt
mit Vielfachheit drei vorkommt. Also gilt
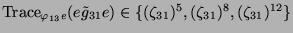 . Von den oben übrig
gebliebenen vier Kandidaten erfüllt dies nur noch ein
Kandidat. Dies ist der Kandidat mit
. Von den oben übrig
gebliebenen vier Kandidaten erfüllt dies nur noch ein
Kandidat. Dies ist der Kandidat mit 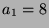 ,
, 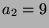 ,
, 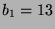 ,
,
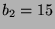 und
und  .
.
Der Brauerbaum ist in Abbildung 3.12
dargestellt.
Abbildung 3.12:
Der Brauerbaum von 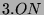 , Primzahl 31, Block 2
, Primzahl 31, Block 2
![\begin{figure}
\begin{center}
\setlength{\unitlength}{0.8mm} \begin{picture}
(...
...makebox(0,0)[b]{\footnotesize\textsf{4}}}
\end{picture} \end{center}\end{figure}](img1191.png) |





Next: Konstruktionen
Up: Primzahl 31, Block 2
Previous: Der Brauerbaum
Inhalt
Index
Markus Ottensmann
2000-02-10
![]() mit der Kondensationsgruppe
mit der Kondensationsgruppe
![]() kondensiert. In der Tabelle
3.43 sind die Zerlegungszahlen des zweiten Blocks
für die Permutationsmoduln und in der Tabelle 3.44
sind die Dimensionen der einfachen kondensierten Moduln des zweiten
Blocks zu sehen. Die Dimension des kondensierten Permutationsmoduls
ist 877. Die Kondensationsalgebra ist
kondensiert. In der Tabelle
3.43 sind die Zerlegungszahlen des zweiten Blocks
für die Permutationsmoduln und in der Tabelle 3.44
sind die Dimensionen der einfachen kondensierten Moduln des zweiten
Blocks zu sehen. Die Dimension des kondensierten Permutationsmoduls
ist 877. Die Kondensationsalgebra ist
![]() .
.
![]() die Spuren auf den
Konstituenten von
die Spuren auf den
Konstituenten von
![]() entsprechend der Tabelle
3.45. In der Tabelle 3.46
sind die Werte
entsprechend der Tabelle
3.45. In der Tabelle 3.46
sind die Werte
![]() der
Spurformel (2.3) für das Element
der
Spurformel (2.3) für das Element
![]() enthalten.
enthalten.
![]() :
: