




Next: 1869-dimensionale Darstellung von über
Up: Konstruktionen
Previous: Das Skript 3ON-L372b
Inhalt
Index
495-dimensionale Darstellung von 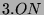 über
über 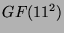
Mit GAP kann man leicht nachrechnen, daß
eine Zerlegung des Permutationscharakters in die gewöhnlichen
irreduziblen Charaktere ist. Also folgt
Nach (4.11) ist bekannt, daß zwei
495-dimensionale Moduln in der Zerlegung des Permutationsmoduls von
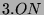 auf 368
auf 368 280 Punkten vorkommen. Um eine 495-dimensionale
Darstellung von
280 Punkten vorkommen. Um eine 495-dimensionale
Darstellung von 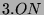 zu erhalten, gehe folgendermaßen vor:
zu erhalten, gehe folgendermaßen vor:
- 1.
- Der Permutationsmodul
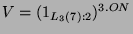 wird
mit der Kondensationsgruppe
wird
mit der Kondensationsgruppe 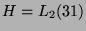 kondensiert. Die benutzte
Kondensationsalgebra ist
kondensiert. Die benutzte
Kondensationsalgebra ist
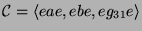 . Dadurch erhält man einen Modul ,,kleiner``
Dimension.
. Dadurch erhält man einen Modul ,,kleiner``
Dimension.
- 2.
- Der kondensierte Modul wird mit dem MeatAxe-Programm
chop in seine Konstituenten zerteilt. Die Dimensionen
der Konstituenten des kondensierten Permutationsmoduls sind in
Tabelle 4.1 aufgelistet.
- 3.
- Im kondensierten
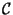 -Modul
-Modul
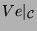 sind
zwei eindimensionale Konstituenten mit Vielfachheit 1. Mit der in
[LMR94] beschriebenen und in MeatAxe implementierten
Methode der Peakwords, erhält man einen Vektor
sind
zwei eindimensionale Konstituenten mit Vielfachheit 1. Mit der in
[LMR94] beschriebenen und in MeatAxe implementierten
Methode der Peakwords, erhält man einen Vektor 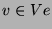 , der zu
einem der kondensierten 495-dimensionalen
, der zu
einem der kondensierten 495-dimensionalen 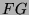 -Moduln gehört.
-Moduln gehört.
- 4.
- Da für einen
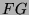 -Modul
-Modul 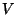 auch
auch
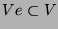 ist, kann
ist, kann 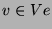 in den kleinsten
in den kleinsten 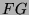 -Teilmodul
-Teilmodul 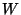 von
von 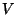 eingebettet werden,
der
eingebettet werden,
der 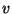 enthält. Bei einem Permutationsmodul wird durch die
Umkehrabbildung von
enthält. Bei einem Permutationsmodul wird durch die
Umkehrabbildung von 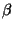 aus (2.4) und durch Bilden von
Bahnensummen diese Einbettung gegeben. Dieser Prozeß wird
unkondensieren genannt.
aus (2.4) und durch Bilden von
Bahnensummen diese Einbettung gegeben. Dieser Prozeß wird
unkondensieren genannt.
Nun wird der Vektor 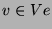 unkondensiert.
unkondensiert.
- 5.
- Der Spinning-Algorithmus, angewendet auf den unkondensierten
Vektor
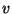 , liefert einen 495-dimensionalen
, liefert einen 495-dimensionalen 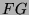 -Modul
-Modul 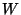 .
.
An der Spur eines Repräsentanten der
Klasse 16a kann man sehen, ob der erhaltene
495-dimensionale 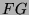 -Modul zu den Charakteren
-Modul zu den Charakteren
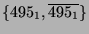 oder
oder
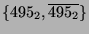 gehört. Durch die Definition des zentralen Elementes
gehört. Durch die Definition des zentralen Elementes
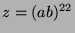 , wobei
, wobei 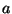 und
und 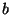 Standarderzeuger von
Standarderzeuger von 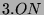 sind, kann
man nun zwischen dem Modul
sind, kann
man nun zwischen dem Modul 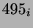 (
(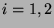 ) und seinem konjugierten
) und seinem konjugierten
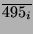 unterscheiden.
unterscheiden.
Tabelle 4.1:
Dimensionen und Vielfachheiten der Konstituenten des
kondensierten Permutationsmoduls
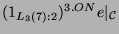 über
über 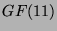 .
.
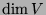 |
 |
Vielfachheit |
| 1 |
1 |
2 |
| 495 |
1 |
1 |
| 495 |
1 |
1 |
10 943 943 |
2 |
1 |
42 687 687 |
4 |
1 |
42 687 687 |
4 |
1 |
20 925 925 |
5 |
2 |
32 395 395 |
5 |
1 |
20 925 925 |
5 |
2 |
37 728 728 |
6 |
1 |
37 728 728 |
6 |
1 |
52 668 668 |
7 |
1 |
26 752 752 |
8 |
1 |
|





Next: 1869-dimensionale Darstellung von über
Up: Konstruktionen
Previous: Das Skript 3ON-L372b
Inhalt
Index
Markus Ottensmann
2000-02-10
![]() auf 368
auf 368![]() 280 Punkten vorkommen. Um eine 495-dimensionale
Darstellung von
280 Punkten vorkommen. Um eine 495-dimensionale
Darstellung von ![]() zu erhalten, gehe folgendermaßen vor:
zu erhalten, gehe folgendermaßen vor:
![]() unkondensiert.
unkondensiert.
![]() -Modul zu den Charakteren
-Modul zu den Charakteren
![]() oder
oder
![]() gehört. Durch die Definition des zentralen Elementes
gehört. Durch die Definition des zentralen Elementes
![]() , wobei
, wobei ![]() und
und ![]() Standarderzeuger von
Standarderzeuger von ![]() sind, kann
man nun zwischen dem Modul
sind, kann
man nun zwischen dem Modul ![]() (
(![]() ) und seinem konjugierten
) und seinem konjugierten
![]() unterscheiden.
unterscheiden.