Zurück zum 30.11.00; weiter zum 07.12.00.
Gegenstand der Vorlesung war die Betrachtung von Mittelpunkten
von Zweiecken im projektiven Raum. Hierzu sollten die bisher gewonnenen
Erkenntnisse über affine Verhältnisse aus projektiver Sicht diskutiert
werden.
Für die Konstruktion des Mittelpunktes eines Zweieckes gelangten
wir zur folgenden vorläufigen Definition.
Definition:
Gegeben sei eine projektive Ebene mit dem projektiven Fano-Axiom (pF)
sowie dem projektiven Desargues-Axiom (pD).
Weiterhin sei gegeben ein Zweieck {A, B} auf der Geraden
z.
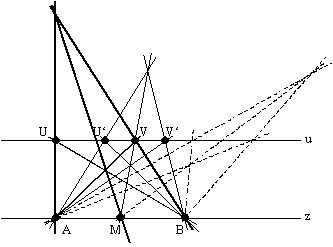
Dann konstruiere man wie folgt:

Es wurde deutlich, daß der so gefundene Mittelpunkt M nicht dem
Mittelpunkt im affinen Raum entspricht.
Daraus ergab sich die Fragestellung, wie M von Wahl der Lage von u,
U und V in obiger Definition abhängig ist.
Zur Klärung führten wir physikalische Experimente durch.
Zunächst wählten wir auf der Geraden u zwei verschiedene Punktpaare
{U, V} und {U', V'}.

Wir folgerten den Satz:
Der so konstruierte Punkt M ist unabhängig von der Wahl der Punkte
U und V auf u.
[Ein Beweis ist möglich mit (pD).]
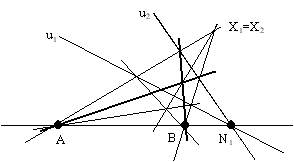
Dann ließen wir zum einen u um ihren Schnittpunkt N mit
der Geraden z rotieren und verschoben zum anderen die Gerade u
parallel, wählten also einen anderen Schnittpunkt mit z, nämlich
N1.
 |
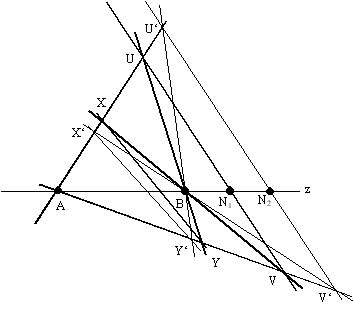 |
Wir folgerten den Satz:
Gehen u1 und u2 durch den selben
Punkt N auf AB = z (mit N ungleich A, B)
und sind U1, U2, V1, V2 so
gewählt, daß X1 = X2 ist
[günstig ist es also, in der Konstruktion zunächst X1
= X2 zu zeichnen], dann liegen die Punkte X, Y1
und Y2 auf einer Geraden. Ihr Schnittpunkt mit z
heißt M := M1 = M2.
[Der Beweis wurde in der Übungsstunde erbracht.]
Die Tatsache, daß die Lage des Mittelpunktes abhängig von der Wahl des Schnittpunktes der Geraden u und z ist, gebar die folgende Definition.
Definition:
Der so in Abhängigkeit von N auf AB (N ungleich
A
und B) definierte Punkt heißt bei uns der
N-Mittelpunkt
von {A, B}.
Zurück zum 30.11.00; weiter zum 07.12.00.