Zurück zum LDfM, zur Fachgruppe Mathematik,
zur Fakultät für Mathematik, Informatik und Naturwissenschaften, zur RWTH.

Grundlagen der Geometrie
Protokoll vom 07.12.00 (ES)

Zurück zum 04.12.00; weiter zum 14.12.00.

Thema: Projektive Sicht des Mittelpunktbegriffes

Definition:
Gegeben ein projektiver Raum mit (pF) und (pD). Zu dem Zweieck $\{A,B\}$ und dem Punkt $N$ mit $N I AB,\ N \not= A,B$ konstruiere den $N$-Mittelpunkt von $\{A,B\}$ so:

Zeichne eine Gerade $u$ durch $N$.

$X \ \not\textit{I} \ u$, $X \not{I} AB$ und $X$ liegt in der Ebene, die durch $AB$ und $u$ aufgespannt wird.

$XA$ und $XB$ werden mit $u$ in der Ebene $AB,u$ geschnitten und es ergeben sich $U$ und $V$.

Dann ist $UB \wedge VA =: Y$ und $XY \wedge AB =: M$.

Satz:
(Vor. (pF), (pD)) $M$ ist unabhängig von der Wahl von $u$ und $X$, aber abhängig von der Wahl von $N$.

Definition:
Ein Quadrupel $(A,B,N,M)$ von vier kollinearen Punkten heißt harmonisch, wenn $M$ der $N$-Mittelpunkt von $\{A,B\}$ ist. [$M$ heißt auch der vierte harmonische Punkt zu $(A,B,N)$.]

Fragen:

• Ist dann auch $(B,A,N,M)$ harmonisch? - Ja (klar).
• Ist dann auch $(A,B,M,N)$ harmonisch? - Ja: studiere Viereck!
• Ist dann auch $(N,M,A,B)$ harmonisch? - Ja. (Gleiche Konstruktion.)

Studiere ,,ebenes Viereck``!
Gegeben sei ein ebenes Viereck $(A,B,C,D)$.
Bilde alle sechs Seiten.
Es ergeben sich drei weitere Schnittpunkte der Geraden, die Diagonalpunkte des ebenen Dreiecks. Wegen (pF) bilden sie ein Dreieck, das Diagonalpunkte-Dreieck (Diagonalpunkte-Dreiseit).
Der Schnitt der drei Dreiecksseiten mit den sechs Vierecksseiten ergeben sechs neue Punkte:

$Y^{\prime}$ und $Y^{\prime\prime}$ auf $XZ$,

$Z^{\prime}$ und $Z^{\prime\prime}$ auf $XY$,

$X^{\prime}$ und $X^{\prime\prime}$ auf $YZ$.

Werden die neuen Punkte miteinander verbunden, dann sind jeweils gewisse drei anscheinend kollinear:

$X^{\prime} Y^{\prime\prime} Z^{\prime\prime}$ =: $b$,

$X^{\prime\prime} Y^{\prime} Z^{\prime\prime}$ =: $d$,

$X^{\prime} Y^{\prime} Z^{\prime}$ =: $a$,

$X^{\prime\prime} Y^{\prime\prime} Z^{\prime}$ =: $c$.

Diese Geraden definieren ein ebenes Vierseit $\{a,b,c,d\}$, wobei $a$ zu $A$ gehört usw. .

Beweis der Kollinearität der Schnittpunkte mit dem Satz von Desargues:
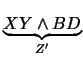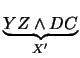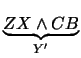$(X,Y,Z) \barwedge_A (B,D,C)$ liefert kollineare Punkte:

$\underbrace{XY \wedge BD}_{Z^{\prime}}$,   $\underbrace{YZ \wedge DC}_{X^{\prime}}$,   $\underbrace{ZX \wedge CB}_{Y^{\prime}}$.

Die Punkte $A$, $B$, $X$ und $X^{\prime\prime}$ liegen auf der Geraden $AB$ und bilden ein harmonisches Quadrupel $(A,B,X,X^{\prime\prime})$. Analog dazu bilden auch die Punkte auf den anderen fünf Seiten des Ausgangsvierseits harmonische Quadrupel.

Frage:
Was passiert per Zentralprojektion mit harmonischen Quadrupeln? - Sie gehen wieder auf harmonische Quadrupel.

Frage:
Gelten auch die dualen Aussagen? Also ist auch (pF)$^*$ und (pD)$^*$ erfüllt? - Die Gültigkeit von (pD)$^*$ wurde bereits nachgewiesen und die Gültigkeit von (pF)$^*$ ist leicht zu zeigen. Demnach gelten die dualen Aussagen in unserer projektiven Ebene ebenfalls!

Eine weitere Frage ist dann nach dem Wortlaut dieser Aussagen.

Definition:
Ein harmonisches Geradenquadrupel $(a,b,n,m)$ ist ein Quadrupel aus vier kopunktalen Geraden, wobei $m$ die $n$-Mittelgerade des (ebenen) Zweiseits $(a,b)$ ist. Dazu:

Definition:
Konstruktion der $n$-Mittelgerade: Ersetze die Großbuchstaben durch Kleinbuchstaben.

Frage:
Wenn $(a,b,n,m)$ ein harmonisches Geradenquadrupel ist und man die Schnittpunkte $(A,B,N,M)$ mit einer Geraden, die nicht durch $S$ geht, bildet, bilden diese dann ein harmonisches Punktequadrupel? - Ja.

Studium von Zentralprojektionen

1. in projektiven Ebenen zwischen zwei Geraden sowie die Hintereinanderausführung.
2. in projektiven Räumen (etwa projektive Dimension 3) zwischen zwei Ebenen sowie die Hintereinanderausführung.
3. ,,Projektivitäten`` von Geraden auf sich selbst bzw. von Ebenen auf sich selbst.

Was hat uns der Exkurs ins Projektive für den affinen Mittelpunktsbegriff gebracht?

Allgemein:

• Interessante Begriffe: harmonisches Punktequadrupel, harmonisches Geradenquadrupel.
• Interessante Sätze: ebenes Viereck, Diagonalpunkte-Dreieck und -Dreiseit, ebenes Vierseit.

Für den affinen Mittelpunktsbegriff:

Gegeben ist eine affine Ebene mit (F) und (D,d). Dann kann diese Ebene in eine umfassende projektive Ebene übertragen werden. Gelten dann (pF) und (pD) auch für diese projektive Ebene? - Vorsicht! Deshalb gehen wir sicherheitshalber von einer affinen Ebene aus, die von einer projektiven Ebene mit (pF) und (pD) herkommt [durch Weglassen einer Geraden und ihrer Punkte].

Eine affine Trapezkonstruktion ($UV \Vert AB$) für den affinen Mittelpunkt, der per Parallelogrammkonstruktion definiert ist, ergibt denselben Mittelpunkt.

Dadurch werden neue Erkenntnisse für die affine Situation erlangt.

Zurück zum 04.12.00; weiter zum 14.12.00.

Zurück zum Seitenanfang, zu Grundlagen der Geometrie,
zur Hauptseite, zum LDfM, zur Fachgruppe Mathematik,
zur Fakultät für Mathematik, Informatik und Naturwissenschaften, zur RWTH.