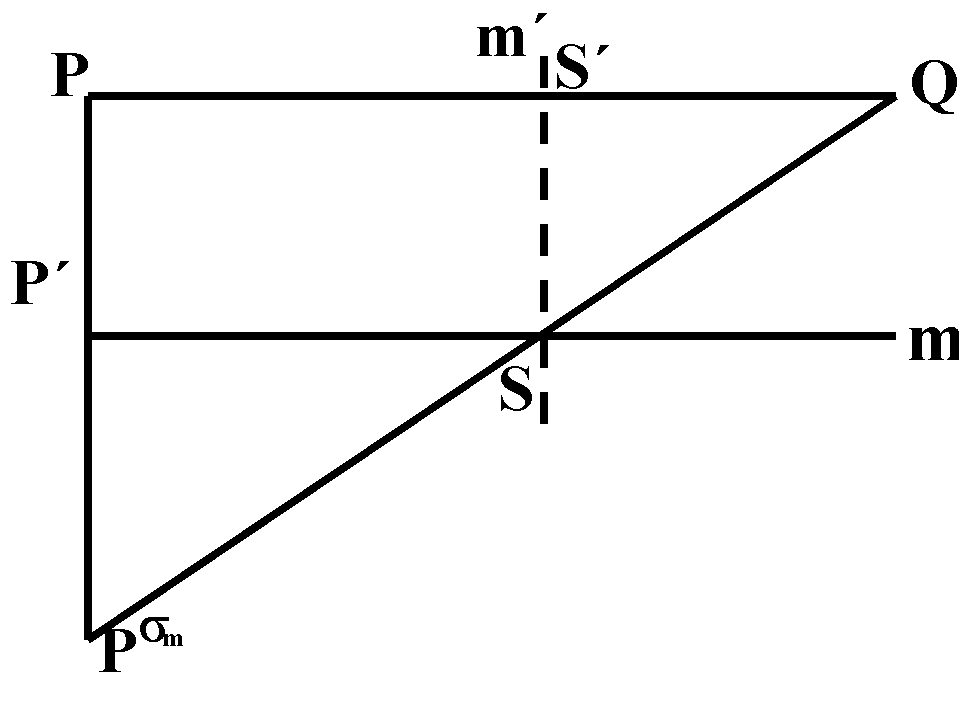Grundlagen der Geometrie
Protokoll vom 5.02.2001 (NMA)

In der heutigen Vorlesung wollen wir die Halbierenden einer Geradenkreuzung weiter untersuchen.

Satz:

Gegeben sei eine affine Ebene mit (F), (D),
^ mit (O1) - (O4),
eine Geradenkreuzung (S, {g, h})
und eine nicht isotrope Halbierende m.

Dann ist das Lot m´ durch S auf m ebenfalls eine Halbierende.

Dieser Satz soll bewiesen werden.
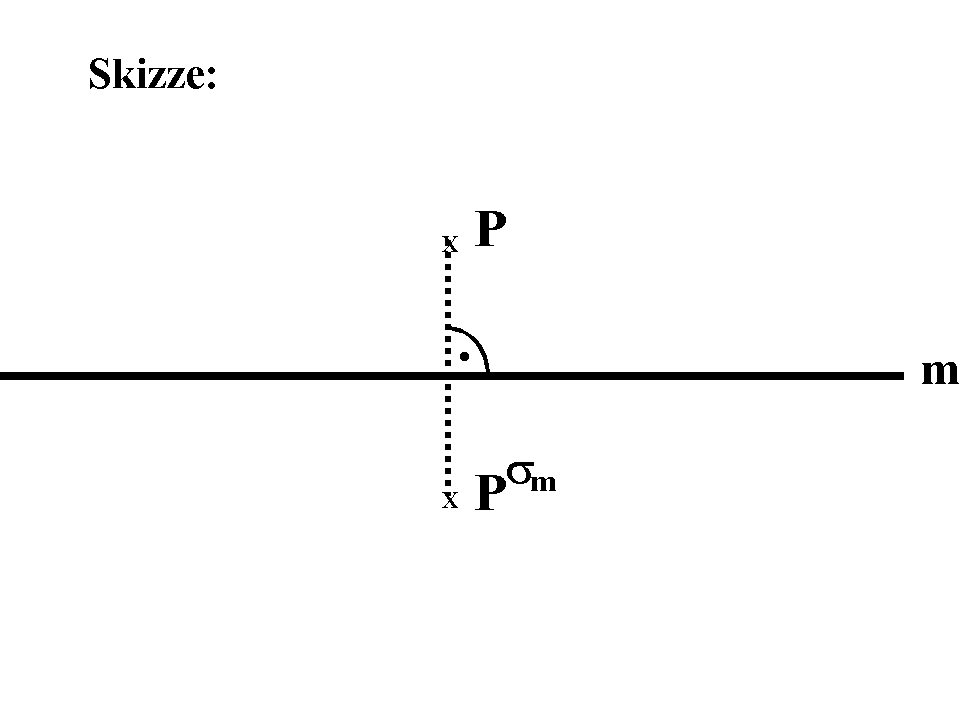
Erinnerung an die Definition der Halbierenden:

Gegeben sei eine affine Ebene mit (F), (D),
^ mit (O1) - (O4),
und eine Geradenkreuzung (S, {g, h}).

Dann heißt eine Gerade m Halbierende,
wenn g^s_m = h ist (falls m nicht isotrop ist).

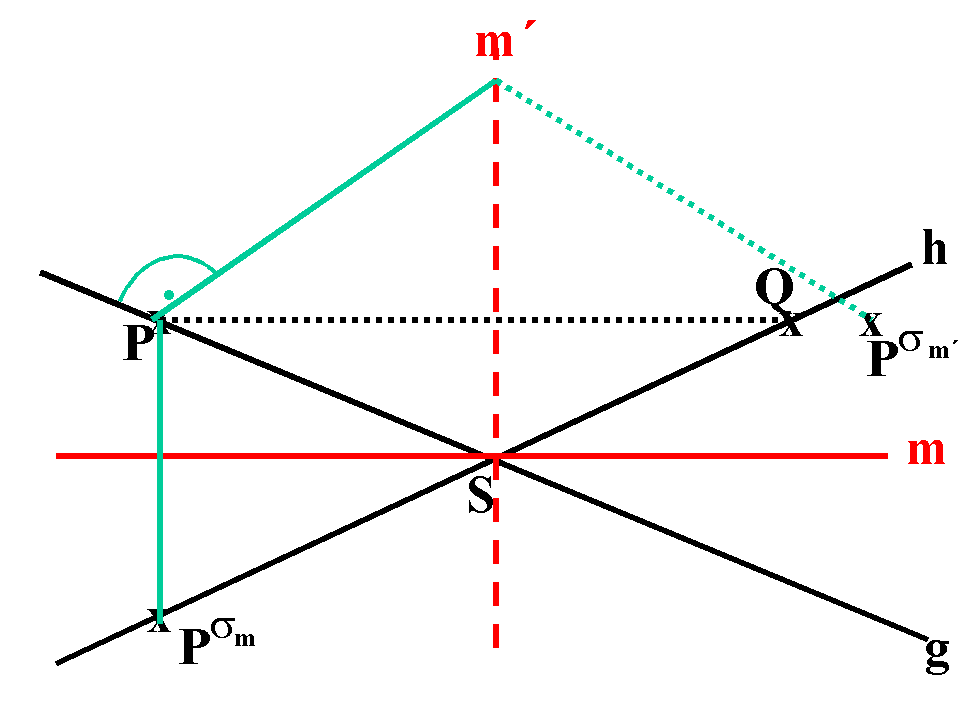
Beweis:

Es sei P I g und P ¹ S.
Nach Voraussetzung ist P^s_m I h.
Q := h Ù Parallele zu m durch P.

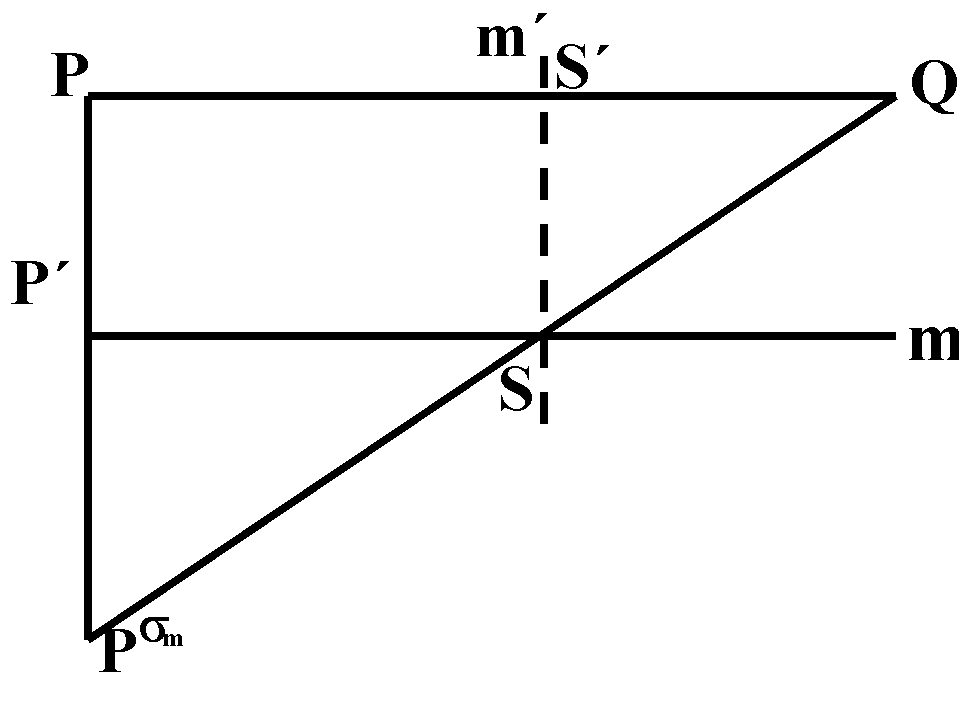MP (P, P^s_m ) sei M.
Nach der Def. von s_m ist
m = MS (P, P^s_m ) parallel PQ
(nach der Def. von Q).
S := MP (P^s_m, Q) (da M durch die
Parallelprojektion längs m auf S geht).
Nach (O3) gilt PM || m´.
S´ := m´ Ù PQ. Also ist S' = MP (PQ)
(Parallelprojektion).
Also ist m´ = MS (P, Q), d.h. g^s_m´ = h, wie gewünscht.

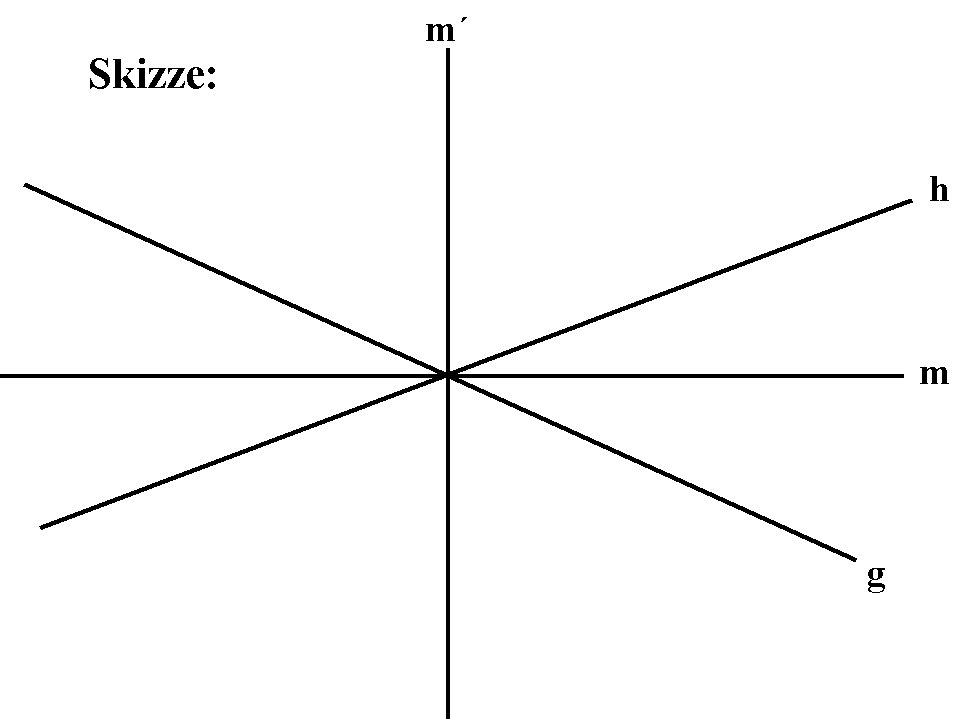
Frage: Schneiden sich die Halbierenden in einem Dreieck?:

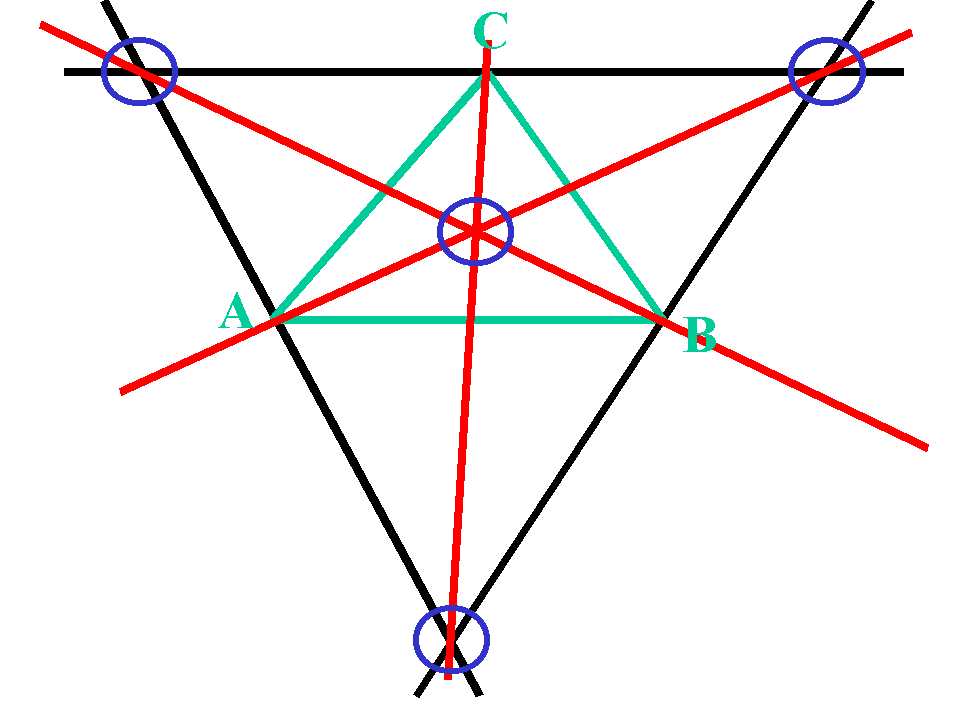
Frage der Existenz:

Gesucht: Gegenbeispiel.
Dazu: Vektorraum mit dem Standardskalarprodukt über Q.
Hier existieren Halbierende nicht unbedingt!
(Dazu mehr in der Vorlesung am 8.2.01.)

Satz:

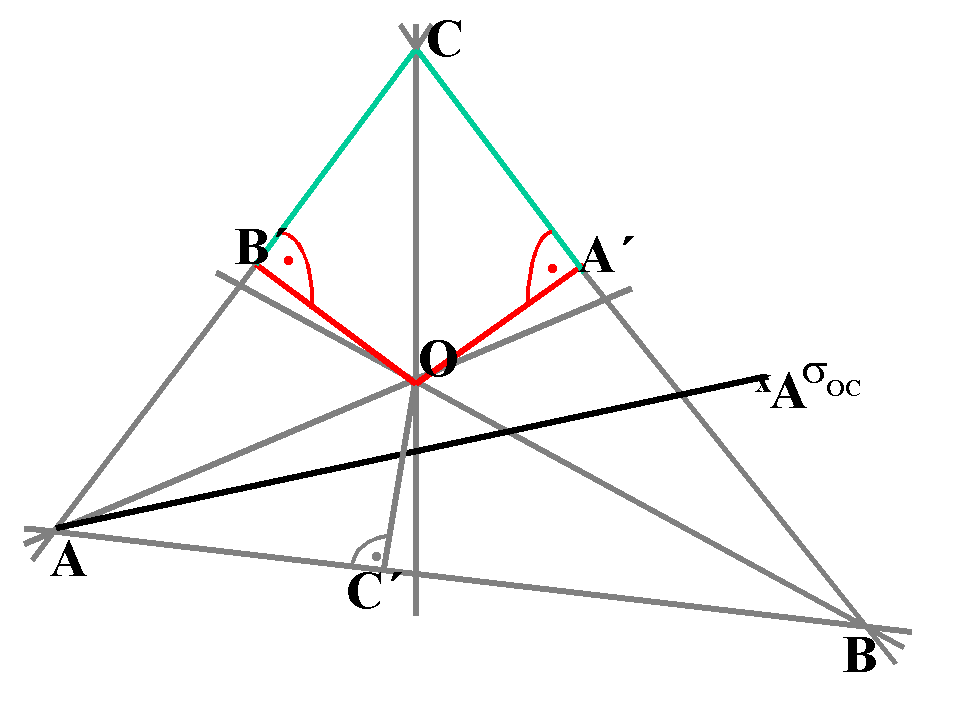
Beweis:
AO ist Halbierende zu A.
BO ist Halbierende zu B.
A', B' und C' seien die Lotfußpunkte von O
auf die nicht isotropen Seiten .
(OB´) ist abstandsgleich zu (OC´).
(OA´) ist abstandsgleich zu (OC´).
Es ist (H) vorausgesetzt. Also ist die
Relation "Abstandsgleichheit" transitiv.
Somit ist (OB´) abstandsgleich zu (OA´).
Also ist OC eine Halbierende durch C.

Zurück zum 1.2.2001;
weiter zur Übungsstunde vom 7.02.01 und zum 8.02.01.