Zurück zum LDfM, zur Fachgruppe Mathematik,
zur Fakultät für Mathematik, Informatik und Naturwissenschaften, zur RWTH.
<b>Grundlagen der Geometrie <br> Protokoll vom 08.02.2001 (HR)<b>

Grundlagen der Geometrie
Protokoll vom 08.02.2001 (HR)

Zurück zum 5.02.01 und zur Übungsstunde vom 7.02.01;
weiter zum 12.02.01.

Thema: Abschließende Betrachtung des Begriffs der Halbierenden.


In der letzten Verlesung wurde folgender Satz noch nicht abschließend behandelt:

Satz:
Gegeben: Es sei A* eine affine Ebene mit (F), (D) und Orthogonalitätsrelation mit (H). Weiter sei {A, B, C} ein Dreieck in A* mit zwei Ecken (etwa A und B), die jeweils eine Halbierende besitzen.
Behauptung: Die beiden Halbierenden schneiden sich in einem Punkt O, und die Gerade durch O und C ist eine Halbierende der Ecke bei C.


Bemerkung: Nach einem Satz aus einer vorigen Vorlesung besitzt eine Ecke, die eine Halbierende hat, auch eine zweite Halbierende, das heißt A und B besitzen jeweils zwei Halbierende. Damit existieren in diesem Dreieck vier Halbierendenschnittpunkte.

Skizze:
(Zum Satz)


Beweis: 1. Schritt: u sei eine Halbierende bei A und v sei eine Halbierende bei B.
Es gilt au = c und cv = b und a b. Dann ist u v [Schnittpunkt O existiert] und u v.
Denn wäre u || v, so wäre au v = b (einerseits), und da u . v eine Translation ist (siehe Hilfsatz unten), wäre b = au v || a. Wäre u v, so wäre u . v Punktspiegelung, also Dilatation. Dies wäre ein Widerspruch zu b || a.
Schritt 2: Siehe letzte Vorlesung.



Hilfssatz: Ist u || v, so ist u . v eine Translation. Ist u v, so ist u . v eine Punktspiegelung.
Skizze:
Beweis: Degen-Profke, Seite 137 und 135.



Es folgen Beispiele (im Rahmen der Analytischen Geometrie).

I. Euklidische Ebene über einem Q-Vektorraum mit positiv definitem Skalarprodukt:

Gegeben sei V = Q x Q, G = Standardskalarprodukt und B = (e1, e2) als Standardbasis.
Damit ist BGB = .
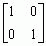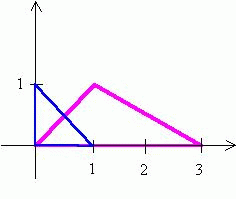Im blauen Dreieck {(0, 0), (1, 0), (0, 1)} existiert bei A eine Halbierende, während bei B keine Halbierende existiert, denn die Existenz führt auf eine Gleichung, die in Q nicht lösbar ist (wohl aber in R). Im lila Dreieck {(0, 0), (3, 0), (1, 1)} existiert keine Halbierende.


II. Minkowski-Ebene über einem R-Vektorraum:


Es sei V = R x R und ein Skalarprodukt G bezüglich der Standardbasis B = (e1, e2) wie folgt gegeben:
BGB = .
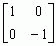Desweiteren sei A die zu V gehörige affine Ebene mit der durch G gegebenen Orthogonalitätsrelation.
Skizze:


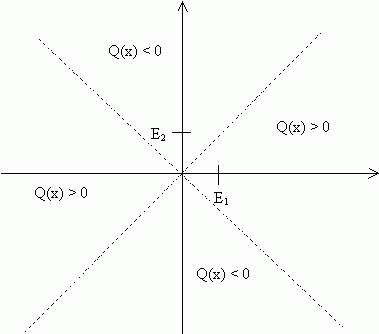
In der Skizze erkennt man die isotropen Richtungen, nämlich die zu den Geraden <e1 + e2> und <e1 - e2>. Es gilt: G(x, x) = x12 - x22 für x = x1 . e1 + x2 . e2.


Definition: Wir nennen nun Q(x) := G(x, x) das "Längenquadrat" von x oder das "Abstandsquadrat" von (0, x). Dabei ist x als der Vektor vom 0-Punkt zum Punkt X zu verstehen. Ein Punkt X heißt raumartig (bezgl. des Ursprungs), wenn Q(x) > 0, zeitartig, wenn Q(x) < 0 ist.



Es stellt sich an dieser Stelle die (in vorigen Vorlesungen bereits gestellte) Frage nach dem Erscheinungsbild eines Kreises in der Minkowski-Ebene. Wir wählen einen Punkt E1 auf einem Kreis mit Mittelpunkt 0, also mit Radius r = (0, E1). Weitere Kreis-Punkte konstruieren wir über Spiegelungen, also mittels isotroper Parallelogramme:


1. Wir wählen eine Gerade g durch den 0-Punkt.
2. Wir konstruieren ein isotropes Parallelogramm so, daß g eine Diagonale und E1 ein Eckpunkt dieses Parallelogramms ist.
3. Die andere Diagonale g| ist dann orthogonal zu g, d.h. der Eckpunkt E3 ergibt sich als E3 = E1g. Da E1 und E3 nach unserer Definition abstandsgleich sind, liegt auch E3 auf unserem Kreis.


Skizze:

Die rosa Linie gibt in dieser Skizze unseren Kreis wieder.

Bis hierher haben wir Halbierende betrachtet, nicht jedoch nach ihrer Existenz gefragt. Deshalb schließt sich nun diese Frage an.



Für welche Kreuzungen (bei 0) gibt es Halbierende?


Sollte die zu untersuchende Kreuzung nicht bei 0 liegen, so überführt eine Translation diese Kreuzung in eine bei 0, und die folgenden Betrachtungen sind möglich.

Gegeben: Eine Kreuzung W = (0, {<a>, <b>}).
1. Fall: a und b sind raumartig:
Per Wahl von a| Î <a> und b| Î <b> erreichen wir (über R), daß Q(a|) = 1 und Q(b|) = 1 ist.


 Es gilt dann G(a - b, a + b) = Q(a) + G(a, b) - G(b, a) - Q(b) = Q(a) + [G(a, b) - G(b, a)] - Q(b) = 1 + [0] - 1 = 0. Damit haben wir unsere "Achse" gefunden, denn sei m := <a + b> so geht m durch den 0-Punkt und auch durch den Mittelpunkt von (A, B), und es gilt Am = B.


2. Fall: a und b sind zeitartig:
Wir wählen hier a| Î <a> und b| Î <b> so, daß Q(a|) = -1 und Q(b|) = -1 ist. Wir vermuten, m := <a + b> liefert uns - analog zu oben - eine Halbierende. Der Beweis wird analog zum 1. Fall geführt.
3. Fall: a ist raumartig, b zeitartig:
Per Wahl von a| Î <a> und b| Î <b> erreichen wir, daß Q(a|) = 1 und Q(b|) = -1 ist.
Wenn <a - b> isotrop ist, exisiert keine Halbierende; also sei ohne Beschränkung der Allgemeinheit <a - b> nicht isotrop.

Zur Bestimmung der zu <a - b> isotropen Richtung wählen wir folgenden Ansatz:

G(a - b, l . a + m . b) = 0.

Die Darstellung l . a + m . b ist dabei sinnvoll, weil B| := (a, b) eine Basis unseres Vektorraums ist.
Damit gilt:
G(a - b, l . a + m . b) = l . (Q(a)) - l . G(b, a) + m . G(a, b) - m . (Q(b))
= l . 1 - m . (-1) + (m - l) . G(b, a))
= m . (1 + G(b, a)) + l . (1 - G(b, a)) = 0.
Offensichtlich ist die Gleichung für m = -(1 - G(b, a)) und l = 1 + G(b, a) erfüllt.

Die gesuchte orthogonale Richtung wäre demnach <(1 + G(b, a)) . a - ((1 - G(b, a)) . b>.

Es gilt andererseits aber M := Mp(A, B): 1/2 . a + 1/2 . b, das heißt die Halbierende, auf der M liegt, hat die Richtung von m = <x . a + x . b>. Daher muß für diese Halbierende nach unserer Rechnung gelten:

1 + G(a, b) = - (1 - G(a, b)).

Diese Aussage ist jedoch äquivalent zu 2 = 0. Es gibt also in diesem Fall keine Halbierende.



Um die Existenz einer Halbierenden zu garantieren, brauchen wir also ein zusätzliches Axiom. Um dieses Axiom sinnvoll formulieren zu können, benötigen wir noch zwei Definitionen:

Definition: Nach Übungsaufgabe 28 hat die Ebene mit Axiomen (F), (D), (P), (H), (M) und einer Orthogonalitätsrelation keine oder genau 2 isotrope Richtungen {i, j}. Daher unterscheiden wir folgende Fälle:
a) In einer Euklid-Ebene heißen alle Geradenkreuzungen gleichartig.
b) Minkowski-Ebene:
Der Koordinatenkörper sei angeordnet (zusätzliches Axiom), i und j mit i j seien isotrope Geraden durch einen Punkt S.

Eine Kreuzung (S, {g, h}) heißt gleichartig, wenn g und h nur "raumartige Punkte bzgl. S" oder wenn g und h nur "zeitartige Punkte bzgl. S" enthalten [außer S].


Definition: Voraussetzungen wie eben.

Wir wählen als Koordinatenkreuz die Kreuzung (S, {i, j}) und auf i und j Einheitspunkte. Damit ist "ein" Koordinatenkörper festgelegt, von dem wir annehmen, daß er angeordnet ist. Ein Punkt P mit Koordinaten (a, b) heißt raumartig bzgl. S, wenn a > 0 und b > 0 oder a < 0 und b < 0 ist.
P heißt zeitartig bzgl. S, wenn a > 0 und b < 0 oder a < 0 und b > 0 ist.
(Eigentlich interessieren uns nur gleichartige Punkte.)


Bemerkung: In der vorher stehenden Definition erkennt man, weshalb der Koordinatenkörper angeordnet sein muß.


Axiom (W): Der Koordinatenkörper ist angeordnet, und
gleichartige Geradenkreuzungen besitzen Halbierende.


Satz: Gegeben sei eine Ebene mit Orthogonalität und den Axiomen (F), (D), (P), (M), (H), (W).

Dann gilt: Durchmesser schneiden einen Kreis, wenn sie gleichartig mit einem den Kreis schneidenden Durchmesser sind.
Skizze:

In der Skizze erkennt man, g und d schneiden den Kreis, d| dagegen nicht.


"Kreise und Halbierende hängen eng zusammen".

Zurück zum 5.02.01 und zur Übungsstunde vom 7.02.01;
weiter zum 12.02.01.

Zurück zum Seitenanfang, zu Grundlagen der Geometrie,
zur Hauptseite, zum LDfM, zur Fachgruppe Mathematik,
zur Fakultät für Mathematik, Informatik und Naturwissenschaften, zur RWTH.