Zurück zum LDfM, zur Fachgruppe Mathematik,
zur Fakultät für Mathematik, Informatik und Naturwissenschaften, zur RWTH.

Grundlagen der Geometrie - Protokoll vom 12.2.2001 Zurück zum 8.02.01;
weiter zur Übungsstunde vom 14.02.01 und zum 15.02.01.

Grundlagen der Geometrie
Protokoll vom 12.2.2001 (NMA+TR)

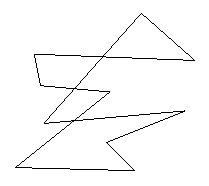
In der heutigen Stunde halten wir den Vortrag mit dem Thema:

Ein/das Inhaltsmaß für Polygone.
(Thema 4)

[Die Marken K1, K2, usw. verweisen auf nachträgliche Kommentare von US am Ende dieser Seite.]

[K1]
Analog zum bisherigen Vorgehen für Abstände [dort: abstandsgleich] in der Vorlesung betrachten wir als erstes den Begriff "inhaltsgleich".

Kongruente Polygone sollen jedenfalls "inhaltsgleich" werden. (Kongruente Polygone lassen sich durch Spiegelungen zur Deckung bringen, und Spiegelungen bilden Punktepaare auf abstandsgleiche Paare ab. Im Moment ist aber noch nicht klar, ob der Inhaltsbegriff (Inhaltsgleichheit) etwas mit dem Abstandsbegriff (Abstandsgleichheit) zu tun hat.)

Dazu:

Definition

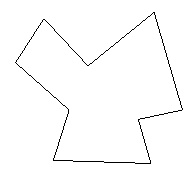
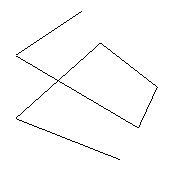
Polygone sind Vereinigungsmengen von endlich vielen abgeschlossenen Strecken.

Beispiele

1.)	2.)	3.)

"normal"	"Abgeschlossenheit?"	"Überschneidungen?"

Frage: (1) Welche Bedingungen müssen gelten, damit wir "normale" Polygone haben? (S. später.)

Es gibt zwei Möglichkeiten, die "Inhaltsgleichheit" zu definieren. Entweder man betrachtet Zerlegungsgleichheit oder Ergänzungsgleichheit.

Definition

Zwei "normale" Polygone heißen zerlegungsgleich, wenn es möglich ist, sie in endlich viele paarweise kongruente "normale" Teilpolygone zu zerlegen.

Frage: (2) Was ist ein Teilpolygon, was bedeutet "Polygon 1 liegt im Innern von Polygon 2"? (S. später.)

Satz

Die Zerlegungsgleichheit ist eine Äquivalenzrelation.

Beweis

Symmetrie: klar. Reflexivität: klar.

Transitivität: Beweisskizze: Polygon A sei zerlegungsgleich mit Polygon B. Polygon B sei wiederum zerlegungsgleich mit Polygon C. Dann kann man durch Übereinanderlegen der Zerlegungen von B eine feinere Zerlegung finden, die sowohl in A als auch in C Zerlegungen mit paarweise kongruenten Polygonen hat. Also ist Polygon A auch zerlegungsgleich mit Polygon C.

Definition

Zwei Polygone heißen ergänzungsgleich, wenn es möglich ist, zu jedem der beiden Polygone endlich viele Polygone so hinzuzulegen, daß die hinzugelegten Polygone paarweise kongruent sind und die so entstandenen Polygone zerlegungsgleich sind.

Satz

Die Ergänzungsgleichheit ist eine Äquivalenzrelation.

Beweis

Der Beweis ist ähnlich dem zur Zerlegungsgleichheit.

Satz

Zwei zerlegungsgleiche Polygone sind stets auch ergänzungsgleich.

Beweis

Nach Definition klar.

Satz (Bolyai, 1833)

Zwei ergänzungsgleiche Polygone sind stets auch zerlegungsgleich.

Der Beweis dieses Satzes ist recht kompliziert und sprengt den Rahmen der Vorlesung.

Nun wollen wir ein Maß für den Inhalt von Polygonen finden. Dafür definieren wir eine Abbildung A von der Menge der "normalen" Polygone F in den Koordinatenkörper K (dessen Eigenschaften wir noch genauer untersuchen werden). [K7]

Bedingungen für das Inhaltsmaß

Für A sollen bestimmte Bedingungen gelten. Es seien F₁, F₂, F Polygone aus F.

(Fl1): Sind F₁, F₂ kongruent, so gilt A(F₁) = A(F₂).
(Fl2): Ist {F₁, F₂} eine Zerlegung von F, so gilt A(F) = A(F₁) + A(F₂).
(Fl3): Wird F₁ von F₂ umschlossen, so ist A(F₁) kleiner oder gleich A(F₂).

Aus diesen Bedingungen folgt auch:

(Fl4): A(F) ist größer oder gleich 0 für alle F.

[K2]

Der Körper K muß also angeordnet sein.

Vorüberlegungen zur Analyse

Es sei eine solche Funktion A gegeben. Betrachten wir zunächst ein Rechteck R und wählen Einheitspunkte auf den "Achsen". Das Einheitsrechteck E mit 0 und den Einheitspunkten als Ecken hat das Maß A(E). Skizze dazu:

Wenn die Endpunkte (Ecken des Rechteckes R) ganzen Zahlen m und n entsprechen, so läß sich jede Seite in Abschnitte der Seitenlänge der zugrundeliegenden Einheitsfläche A(E) zerteilen, und man erhält nach (Fl2) (leicht zu sehen) das Flächenmaß A(R) = m * n * A(E) (blaue Skizze).
Wenn die Endpunkte rationalen Zahlen p und q entsprechen, dann kann man durch weiteres Teilen der Einheitsfläche die Gesamtfläche in Bruchstücke zerlegen, und man erhält A(R) = p * q * A(E) (grüne Skizze).
Wenn die Endpunkte reellen Zahlen entsprechen, dann kann man das Flächenmaß durch eine Intervallschachtelung finden (analog: Ober- und Untersumme beim Integral), man erhält eine Zahl l * m * A(E) (rote Skizze).
[K3]

Es macht daher Sinn, als Koordinatenkörper die Menge der reellen Zahlen zugrundezulegen.

[K4]

Für Rechtecke soll das Flächenmaß das Produkt der Seitenlängen a * b sein. [K5]
Für Parallelogramme soll das Flächenmaß das Produkt aus Grundseitenlänge und Höhe sein (wie aus der Schule bekannt): g * h. [K6] Es muß unabhängig von der Wahl von Grundseite und Höhe sein.
Für Dreiecke soll das Flächenmaß die Hälfte des Produktes aus Grundseitenlänge und Höhe sein (ebenfalls aus der Schule bekannt): 1/2 * g * h. Auch hier soll das Maß unabhängig von der Wahl der Grundseite und der Höhe sein.

Satz

Ein Polygon läßt sich triangulieren, d. h. es gibt eine Zerlegung durch "Diagonalen" [Def.?] aus lauter Dreiecken, die Triangulierung.

Beweisskizze (Induktionsbeweis)

Als Induktionsverankerung betrachte man ein Dreieck, hier gibt es mindestens eine Zerlegung, nämlich das Dreieck selbst. Nun seien die Polygone bis zum n-Eck triangulierbar. Zerlegt man ein (n + 1)-Eck durch "innere Diagonalen" in zwei Polygone, so haben diese weniger als n + 1 Ecken, also höchstens n. Diese Polygone lassen sich also triangulieren. Damit gibt es dann also eine Triangulierung für das (n + 1)-Eck.

Das Flächenmaß eines Polygons soll die Summe der Flächenmaße der Dreiecke einer seiner Triangulierungen sein. Das Maß ist unabängig von der Wahl der Triangulierung.

Frage: (3) Wie zeigt man die Eindeutigkeit des jeweiligen Flächenmaßes? (S. später.)