Zurück zum
LDfM, zur Fachgruppe Mathematik,
zur Fakultät
für
Mathematik, Informatik und Naturwissenschaften,
zur RWTH.
Zurück zum
11.01.01
;
weiter zur Übungsstunde vom
17.01.01
und zum
18.01.01.
Grundlagen der Geometrie, Protokoll vom 15.1.2001
Grundlagen der Geometrie
Protokoll vom 15.1.2001 (TR)
Bemerkung:
Die in der Vorlesung benutzten griechischen Buchstaben für Dilatationen, Translationen etc. habe ich
durch entsprechende lateinische Buchstaben ersetzt (z. B. anstatt "Tau" habe ich t
benutzt), da die griechischen Buchstaben in den wenigsten Browsern korrekt angezeigt werden.
Kollineationen affiner Ebenen in axiomatischer Sicht
Gegeben: Eine affine Ebene A.
Hilfssatz 1:
Es gibt höchstens eine Dilatation, die ein Punktepaar aus zwei (!) Punkten auf ein anderes abbildet.
Satz:
Die Translationen bilden eine Untergruppe T(A).
Beweis:
t1, t2 seien Translationen: d := t1
t2 ist Element von Dil(A).
1. Angenommen, d hat den Fixpunkt P.
Mit d t2-1 = t1 ist
Pt2-1 = Pt1 =: P'. Ohne
Beschränkung der Allgemeinheit sei t1 nicht die Identität, also P
ungleich P'.
Hilfssatz 2:
Gegeben sei eine Translationt ungleich id, ein Punkt P, eine Gerade r :=
PPt.
- Ist QIr, so auch Qt.
- Liegt Q nicht auf r, so ist
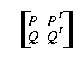 ein
Parallelogramm. ein
Parallelogramm.
Beweis:
Zu a.: Es sei Q ungleich P, also r = PQ und rt =
PtQt || r. Da t eine Dilatation ist, ist r =
rt.
Zu b.: Es liege Q nicht auf r. Nach dem Veblen-Young-Axiom ist
PtQt || PQ [fertig] oder PtQt schneidet
PQ (der Schnittpunkt sei W). Definiere s := QQt, dann ist s =
st und W der Schnittpunkt von r und s. Damit wäre
Wt als Schnittpunkt von rt und st gleich dem
Schnittpunkt von r und s, also W. Dies ist aber ein Widerspruch zur Voraussetzung,
daß t nicht die Identität ist.
|
Sowohl die Translation t2-1 als auch die Translation t1 bilden
Punkte Q, die nicht auf r liegen, auf den vierten Parallelogrammpunkt in 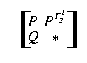 =
= 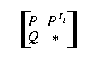 ab. Somit gilt (nach
Hilfssatz 1) t2-1 = t1 und d = t1 t2 =
id, d. h. d liegt in T(A).
ab. Somit gilt (nach
Hilfssatz 1) t2-1 = t1 und d = t1 t2 =
id, d. h. d liegt in T(A).
2. Angenommen d hat keinen Fixpunkt. In diesem Fall ist d eine Translation und in T(A)
enthalten.
Folgerung (Hilfssatz 3):
Zu P, P' existiert höchstens eine Translation t mit Pt = P'.
Beweis:
Folgt aus Hilfssatz 2.
Satz:
Gibt es Translationen in zwei Richtungen, so ist die Translationsgruppe kommutativ.
Beweis:
t1, t2 seien Translationen (die nicht die Identität sind) in verschiedene
Richtungen: PPt1 ist dann ungleich PPt2.
t, t' seien beliebige Translationen [zu zeigen: t t' = t' t].
- 1. Fall:
- t, t' haben verschiedene Richtungen. Qt' = Rt ist
der vierte Parallelogrammpunkt. D. h. Pt' t = Pt t'. Somit ist t t' = t'
t.
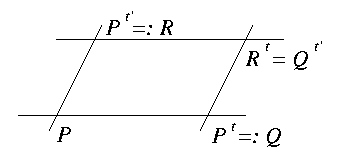
- 2. Fall:
- t, t' haben dieselbe Richtung. Es gibt eine Translation a mit anderer
Richtung (Voraussetzung). Somit gilt
- a t' = t' a,
- a t = t a.
Aber auch t' und a t haben verschiedene Richtungen:
- t' (a t) = (a t) t'.
Deshalb: a (t t') = (a t) t' = t' (a t) = (t' a) t = (a t') t = a (t t'), also t t' = t'
t.
Satz:
Die Untergruppen T(A) und Dil(A) bilden einen Normalteiler von Koll(A).
Beweis:
- Für Dilatationen d und Kollineationen k ist auch dk := k-1 d
k eine Dilatation [zu zeigen: gdk || g]. Setze h :=
gk-1, hd || h, da d Dilatation ist,
gk-1 d || gk-1. k anwenden:
gk-1 d k || g. Somit ist dk in Dil(A)
enthalten. D. h. Dil(A) ist Normalteiler von Koll(A).
- t Translation. Angenommen Wt k = W. Dann ist
(Wk-1)t k = W, also (Wk-1)t =
Wk-1. Dies ist ein Widerspruch, da t keinen Fixpunkt besitzt.
Satz:
Für affine Räume sind äquivalent:
- T(A) ist transitiv.
- (d).
Beweis:
- Von 2. nach 1.:
- Gegeben sei ein Punktepaar (P, Q). O. B. d. A. sei Q ungleich
P (sonst ist id geeignet). [Suche Translation t mit Pt = Q.] Für
alle Punkte X, welche nicht auf PQ liegen, erkläre eine Abbildung f durch
Xf = vierter Parallelogrammpunkt in
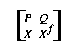 . Für
alle Y, die nicht auf P'Q' liegen, erkläre eine Abbildung f' durch
Yf' = vierter Parallelogrammpunkt in
. Für
alle Y, die nicht auf P'Q' liegen, erkläre eine Abbildung f' durch
Yf' = vierter Parallelogrammpunkt in 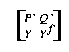 .
.
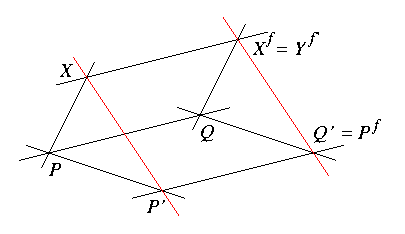
(Es sei P' nicht auf PQ und Q' = P'f.) Es folgt Xf = Yf' für X = Y
nach (d).
- Von 1. nach 2.:
- Klar.
Somit haben wir eine wohldefinierte Abbildung t [via f, f'] auf A. Mit f'
folgt
Pt = Q. [Zu zeigen wäre noch: t ist Translation.]
Analog kann man (vielleicht) zeigen:
- Es gibt zu kollinearen Punkten Z, P, Q höchstens eine Streckung s mit Zentrum
Z und Ps = Q.
- Für affine Räume sind äquivalent:
- Zu kollinearen Punkten P, Z, Q (paarweise verschieden) gibt es eine Streckung s mit
Zentrum Z und Ps = Q.
- (D).
Zurück zum
11.01.01
;
weiter zur Übungsstunde vom
17.01.01
und zum
18.01.01.
Zurück zum
Seitenanfang,
zu
Grundlagen der Geometrie,
zur Hauptseite,
zum LDfM,
zur Fachgruppe Mathematik,
zur Fakultät
für
Mathematik, Informatik und Naturwissenschaften,
zur RWTH.
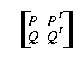 ein
Parallelogramm.
ein
Parallelogramm.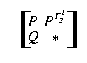 =
= 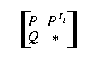 ab. Somit gilt (nach
Hilfssatz 1) t2-1 = t1 und d = t1 t2 =
id, d. h. d liegt in T(A).
ab. Somit gilt (nach
Hilfssatz 1) t2-1 = t1 und d = t1 t2 =
id, d. h. d liegt in T(A).
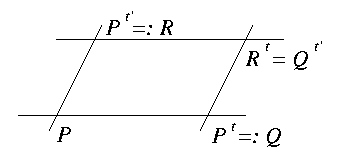
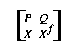 . Für
alle Y, die nicht auf P'Q' liegen, erkläre eine Abbildung f' durch
Yf' = vierter Parallelogrammpunkt in
. Für
alle Y, die nicht auf P'Q' liegen, erkläre eine Abbildung f' durch
Yf' = vierter Parallelogrammpunkt in 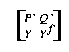 .
.