| Begriff |
genaue Bedeutung |
| Quadrat |
Ein Viereck {A, B, C, D}, bei dem die folgenden Geraden den Bedingungen AB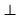 BC, BC BC, BC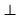 CD, CD CD, CD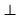 DA, DA DA, DA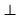 AB, DC AB, DC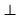 DB genügen, wobei DB genügen, wobei 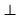 "steht orthogonal auf" bedeutet. "steht orthogonal auf" bedeutet.
Skizze:
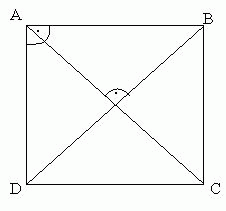
|
| Flächengleichheit |
Wann sind zwei Flächen (flächen)gleich?
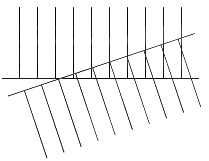
Wir betrachten das Beispiel Dreieck:
Skizze:
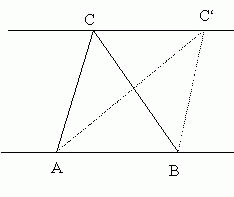
Die Flächengleichheit kann hier axiomatisch eingeführt werden:
Fläche von ABC = Fläche von ABC', falls gilt:
AB || CC'.
|
| g= 90° |
Was ist 90°?
90 ist ein Zahlenwert, ° eine Einheit. Beides zusammen wird als Größe bezeichnet.
|
| a |
Es stellt sich die Frage: Ist a nun die Gerade BC, der Abstand |BC| (eine Größe) oder eine Zahl?
Da in der algebraischen Darstellung a2 verwendet wird, kann die Gerade ausgeschlossen werden, denn das Quadrat
einer Geraden ist unsinnig. Möglich bleibt die Zahl und die Größe. Da a durch Vergleich mit einem "Urmeter" [Einheit: 1m = ein Meter] bestimmt werden kann, ist a offensichtlich eine Größe.
|
| Fläche [als Größe] |
Eine Fläche wird, analog zur Länge, durch
Vergleich mit einem "Urmaß" charakterisiert. Dazu definierten
wir unser "Flächenurmaß" q als das eines
Quadrats mit der Kantenlänge ein Meter.
Wenn q unser "Urflächenmaß" (:= Einheit) ist, so gilt:
{l. q | l Î Q} ist die Menge der
möglichen Größen. (Q kann dabei durch R, C... ersetzt werden.)
Es handelt sich offenbar um einen
eindimensionalen Vektorraum (mit einer Basis m).
In der Physik wird
dieses q offenbar als m2 geschrieben, wobei m unser "Längenurmaß" ein Meter ist. Warum ist dies legitim?
Diese Vereinbarung, m2 als Einheit hinter eine Flächenmaßzahl zu schreiben, ist dadurch entstanden,
daß die Maßzahl für eine Fläche durch Multiplikation
der Maßzahlen für Länge und Breite eines Rechtecks
berechnet wird.
Bei einem Quadrat wird die Maßzahl für die Breite (= Länge)
quadriert, und somit ist das quadrieren der Einheit die logische
Fortsetzung des Quadrierens der Maßzahlen. Wenn
man das Assoziativgesetz und das Distributivgesetz für das "Produkt"
von Längenmaßen verwendet, erhält man das richtige
Flächenmaß, wenn man statt m2 wieder q
schreibt.
Mit diesem Wissen läßt sich die Frage nach der
mathematischen Natur des Quadrats einer Größe beantworten. Es gilt:
(l. m)2 = l2 . m2,
wobei l2 sich in der entsprechenden Struktur (z. B. Q) berechnen läßt. m2 stellt dagegen ein Tensorprodukt dar.
|
| Kongruenzsatz |
Alle drei Seiten zweier Dreiecke sind genau dann gleichlang, wenn die beiden Dreiecke deckungsgleich (:= kongruent) sind.
|