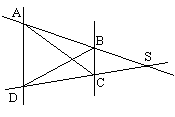
Das Veblen-Young Axiom: Es sei {A, B, C, D} ein Viereck (Menge von vier Punkten von denen je drei nicht kollinear sind) in P.
 Die
Geraden AB, CD seien nicht windschief* und BC, DA
seien nicht windschief**.
Die
Geraden AB, CD seien nicht windschief* und BC, DA
seien nicht windschief**.
[Z. z.: BD, AC sind nicht windschief***].
Zurück zum 26.10.00; weiter zum 02.11.00.
In der Übungsstunde wurde die erste Aufgabe von Blatt 1 bearbeitet.
Wie soll an Übungsaufgaben herangegangen werden?
Zu 1)
| Affiner Raum über einen
Vektorraum:
V Links- Vektorraum über Schiefkörper, P = V, G = Menge aller Restklassen nach 1- dimensionalen Teilräumen, I = Elementsein, g || h, wenn g, h Restklassen nach demselben Teilraum sind. |
Affiner Raum:
(P, G, I, || ) mit I1 – I3, A1 – A3. |
Für affine Räume über Vektorräumen sind I1
– I3, A1 – A2 bereits bewiesen. Noch zu
zeigen ist A3 (Veblen-Young Axiom).
Dann ist diese Struktur ein affiner Raum im Sinne der Axiome.
Zu 2)
In diesem Beispiel wird versucht, mit Hilfe der Analytischen Geometrie,
d. h. Algebra, die Aufgabe zu lösen.
Zu 3)
Das Veblen-Young Axiom: Es sei {A, B, C, D}
ein Viereck (Menge von vier Punkten von denen je drei nicht kollinear sind)
in P.
 Die
Geraden AB, CD seien nicht windschief* und BC, DA
seien nicht windschief**.
Die
Geraden AB, CD seien nicht windschief* und BC, DA
seien nicht windschief**.
[Z. z.: BD, AC sind nicht windschief***].
Für den Beweis sind drei Fälle zu betrachten:
- AB || CD und BC || DA.
- AB Ù CD existiert und es ist BC || DA oder analog BC Ù DA existiert und es ist AB || CD.
- AB Ù CD und BC ÙDA existieren.
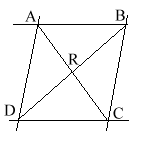
Um nun zeigen zu können, daß BD und AC nicht
windschief sind, benötigen wir einen Weg, unser geometrisches Problem
in die Algebra zu übertragen, da wir dort sowohl Punkte durch Definition
eines Nullpunktes als auch Seiten durch Vektoren ausdrücken und somit
die dort geltenden Rechenregeln benutzen können.
Einschub: "Affiner Raum" im Sinne der LA I:
Vektoren gehören in die Algebra. Wir benötigen "Vektoren abtragen"
in der Geometrie:
Übertragung auf unser Problem:
(Um von Punkten zu Vektoren zu kommen, muß ein Ursprung gewählt
werden. Dann braucht nur noch in V gerechnet werden.).
Neue sprachliche Ebene (affine Räume im Sinne der LA I):
Einschub über Parallelogramme:
Frage am Schluß der Übungsstunde: Wie können die
Äquivalenzklassen dargestellt werden?
* v : P ® P (1-
stellige Operation auf P) für jedes v ÎV
(Translation).
Regeln: 1) (X * v) * w
= X * (v + w).
2) Jedes * v ist Bijektion auf P.
3) P * : V® P ist Bijektion
für alle P Î P
(d. h. Punkte entsprechen Vektoren bei Wahl
eines Nullpunkts / Ursprungs).
(P, V, {* v | v ÎV})
mit Regeln 1- 3 ist ein affiner Raum im Sinne der LA I.
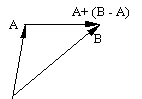
Bei uns sind Punkte Vektoren.
* B bedeutet Addition, d. h. * B : = + B.
![]() ist dann B – A.
ist dann B – A.
Wähle "Ursprung" A; d. h. ersetze Punkte X durch
Vektoren ![]() ÎV.
ÎV.
[(Idee) Drücke alle uns interessierenden Vektoren in ![]() und
und ![]() als Linearkombinationen
aus! ].
als Linearkombinationen
aus! ].
Die Folge (![]() ,
,![]() )
ist linear unabhängig, da {A, B, D} (als Teil
eines Vierecks) ein Dreieck ist.
)
ist linear unabhängig, da {A, B, D} (als Teil
eines Vierecks) ein Dreieck ist.
[Z. z.: ![]() ; Eigenschaft
von "Parallelogrammen"].
; Eigenschaft
von "Parallelogrammen"].
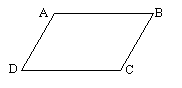
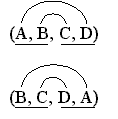 Es
gibt 24 Quadrupel (mit verschiedenen Punkten) aus diesen vier Punkten.
Jeweils acht davon sollten das
selbe Parallelogramm beschreiben. Die beiden links gezeigten Quadrupel
stellen zwei dieser acht Quadrupel dar, die das selbe Parallelogramm ergeben
sollen. Die gebogenen und geraden Verbindungslinien bedeuten hier, daß
AB
parallel zu CD und AD parallel zu BC ist (oben) und
daß BC parallel zu DA und BA parallel zu CD
ist (unten).
Es
gibt 24 Quadrupel (mit verschiedenen Punkten) aus diesen vier Punkten.
Jeweils acht davon sollten das
selbe Parallelogramm beschreiben. Die beiden links gezeigten Quadrupel
stellen zwei dieser acht Quadrupel dar, die das selbe Parallelogramm ergeben
sollen. Die gebogenen und geraden Verbindungslinien bedeuten hier, daß
AB
parallel zu CD und AD parallel zu BC ist (oben) und
daß BC parallel zu DA und BA parallel zu CD
ist (unten).
Zurück zum
26.10.00; weiter zum
02.11.00.
Zurück zum
Seitenanfang,
zu
Grundlagen der Geometrie,
zur Hauptseite,
zum LDfM,
zur Fachgruppe Mathematik,
zur Fakultät
für
Mathematik, Informatik und Naturwissenschaften,
zur RWTH.