Zurück zum
LDfM, zur Fachgruppe Mathematik,
zur Fakultät
für
Mathematik, Informatik und Naturwissenschaften,
zur RWTH.
Grundlagen der Geometrie, Protokoll vom 27. November 2000
Grundlagen der Geometrie
Protokoll vom 27.11.2000 (TR)
Zurück zum
23.11.00;
weiter zum
30.11.00.
Thema: Mittelpunkte in affinen und projektiven Räumen
In der letzten Sitzung wurden u. a. Aussagen über affine Räume
formuliert (die erfüllt sein können oder nicht).
Zunächst jedoch eine Definition:
Definition:
- Ein geordnetes Dreieck ist eine Folge (A, B, C) der
Ecken eines Dreiecks {A, B, C}.
- Ein geordnetes Dreiseit ist eine Folge (a, b, c) der
Seiten eines Dreiseits {a, b, c}.
- Zu einem geordneten Dreieck (A, B, C) gehört das geordnete
Dreiseit (a, b, c), wobei a = BC, b = CA, c = AB gesetzt
ist. Zu einem geordneten Dreiseit (a, b, c) gehört das geordnete
Dreieck (A, B, C), wobei A = bc (Schnittpunkt von b
und c), B = ac, C = ab
gesetzt ist.
Weitere Aussagen über einen affinen Raum:
- (d)
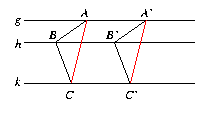
- Für jedes Paar geordneter Dreiecke (A, B, C) und (A', B',
C') gilt: Sind g, h, k drei (!) parallele Geraden mit A,
A' auf g, B, B' auf h, C, C' auf k, so daß zwei Paare
entsprechender Seiten des zugehörigen Dreiseits parallel sind, dann ist
auch das dritte Paar entsprechender Seiten parallel. Skizze:
[Die Aussage gilt in A(V) offenbar nicht für den Fall, daß zwei der Geraden g, h,
k zusammenfallen, betrachte dazu die folgende Skizze:
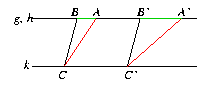
Die rot gezeichneten Geraden sind in diesem Fall nicht parallel!]
- (D)
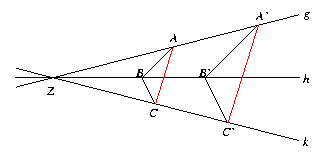
- Für jedes Paar geordneter Dreiecke (A, B, C) und (A', B',
C') gilt: Sind g, h, k drei kopunktale Geraden [durch
einen Punkt Z] und A, B, C, A', B', C' Punkte
mit A, A' auf
g, B, B' auf h, C, C' auf k, so daß zwei Paare entsprechender
Seiten des zugehörigen Dreiseits parallel sind, dann ist auch das dritte
Paar entsprechender Seiten parallel. Skizze:
[Was passieren kann, wenn z. B. A = A' = Z ist, zeigt die
folgende Skizze:
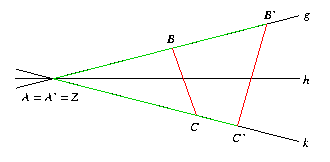
Wie man sieht, sind die rot gezeichneten Geraden nicht parallel!]
- (d und D)-1
- Für jedes Paar geordneter Dreiseite (a, b, c) und (a', b',
c') gilt: Sind die Paare entsprechender Seiten parallel, und
entsprechende Ecken der zugehörigen Dreiecke voneinander verschieden, so
gehen die Verbindungsgeraden entsprechender Ecken der zugehörigen
Dreiecke durch einen Punkt [Z] oder sie sind (alle drei)
parallel. Skizze:
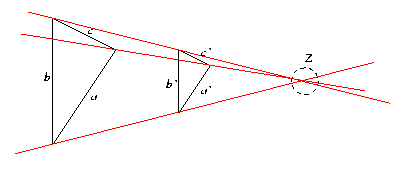
Zitat:
Zwischen den bisher genannten Aussagen bestehen
für affine Ebenen (auch für affine Räume?)
die folgenden Beziehungen:
(p) folgt aus (d),
(d) folgt aus (D),
(D) folgt aus (P),
(D) ist äquivalent zu (d und
D)-1.
[(D) geht auf Desargues (17. Jhd.) zurück, (P) auf Pappos
(ca. 300 n. Chr.).]
Eindeutigkeitssatz für Mittelpunkte via Parallelogramm-Konstruktion in
affinen Räumen
Gegeben ist ein affiner Raum R = (P, G, I,
||) mit Fano-Axiom (F) und Desargues-Axiom (D).
[(D) ist in affinen Räumen mit windschiefen
Geraden immer erfüllt.] Dann ist der Mittelpunkt eines Zweiecks via
Parallelogramm-Konstruktion eindeutig bestimmt.
Beweis:
Zunächst eine Skizze der (rämlichen) Situation:
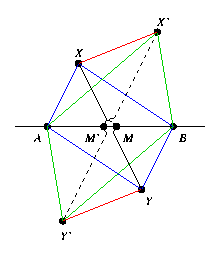
Zu zeigen ist M = M'. Der Skizze nach haben wir die Vermutung
XX' ||
YY'. Ist dies gegeben, dann ist der Beweis mit (d und D)-1
(folgt aus (D)) fertig.
Betrachte die Parallele p zu XX' durch Y. Konstruiere
zusätzliche Parallelogramme 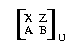 und
und 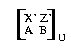 .
Siehe dazu auch folgende Skizze:
.
Siehe dazu auch folgende Skizze:
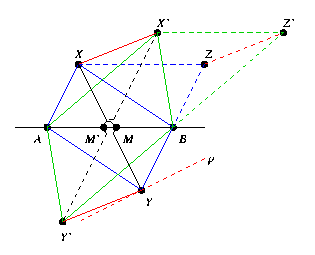
Nach dieser Konstruktion ist XZ || AB || X'Z'. Setze g
= XZ, h = AB, k = X'Z'.
Bei den geordneten Dreiecken (A, X, X') und (B, Z, Z') sind
zwei Paare entsprechender Seiten der zugehörigen Dreiseite parallel, wobei die
Verbindungsgeraden entsprechender Ecken [nämlich g, h, k]
parallel sind. Aus
(d) [(D) impliziert (d), siehe Zitat] folgt: XX' || ZZ', also
p || ZZ'.
Nach dem Parallelenaxiom sind Z, B, Y kollinear, ebenfalls Z', B,
Y'. Nach dem affinen Veblen-Young-Axiom ist das Geradenpaar (p,
Z'BY') nicht windschief und wegen Z' nicht parallel, also existiert
ein Schnittpunkt
Y- =
p(Z'BY').
Vergleiche nun (A, X, X') mit (B, Y, Y-):
Die entsprechenden
Seitenpaare des zugehörigen Dreiseits sind parallel: AX || BY,
AX' || BY' = BY-, XX' || YY-
= p. Aus (d und
D)-1 [folgt aus (D)] folgt: entsprechende Verbindungsgeraden AB,
XY, X'Y- sind parallel oder kopunktal. Da die Parallelität zur Tatsache
(AB)(XY) = M steht, existiert ein gemeinsamer Schnittpunkt M:
M liegt auf X'Y-. Die
geordneten Dreiecke (B, X, X') und (A, Y, Y-)
sind "zentral" mit "Zentrum"
M. Zwei Seitenpaare entsprechender Seiten sind parallel: BX ||
AY, XX' || YY-.
Also [wg. (D)] ist auch das
dritte Seitenpaar parallel: BX' || AY-.
Nach dem Parallelenaxiom ist
AY- = AY' [wg. BX'
|| AY'].
Es folgt Y- = (AY-)(BY') = (AY')(BY') = Y'.
Also ist M = M'.
Neues Verständnis durch projektive Sicht
Die Aussagen über einen affinen Raum sollen demnächst in Aussagen über
einen projektiven Raum übertragen werden.
Zurück zum
23.11.00;
weiter zum
30.11.00.
Zurück zum
Seitenanfang,
zu
Grundlagen der Geometrie,
zur Hauptseite,
zum LDfM,
zur Fachgruppe Mathematik,
zur Fakultät
für
Mathematik, Informatik und Naturwissenschaften,
zur RWTH.






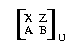 und
und 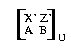 .
Siehe dazu auch folgende Skizze:
.
Siehe dazu auch folgende Skizze: