Grundlagen der Geometrie
Protokoll vom 31.01.2001 (NMA)

Wir formulieren folgenden
- Hilfssatz: i) Aus (P, Q, R₁) ~ (P, Q, R₂) folgt R₁ = R₂.
ii) Das Bild von R´´ in K_{0, 1} ist unabhängig von den verwendeten Parallelprojektionen.
Beweis: Zu i) Selbst.
Zu ii) D.h.: Die Schiefkörper K_{P, Q} und K _{P´, Q´} sind (kanonisch) isomorph.
D.h. spezieller: Die Parallelprojektion längs 11´ ist ein
Schiefkörper-Isomorphismus.
Dazu: 1) Bijektion? O.K.!
2) 0p = 0? O.K.!
1p = 1? O.K.!
3) Aus a + b = c folgt a p + b p = c p?
4) Aus a * b = c folgt a p * b p = c p?

Zu 4)
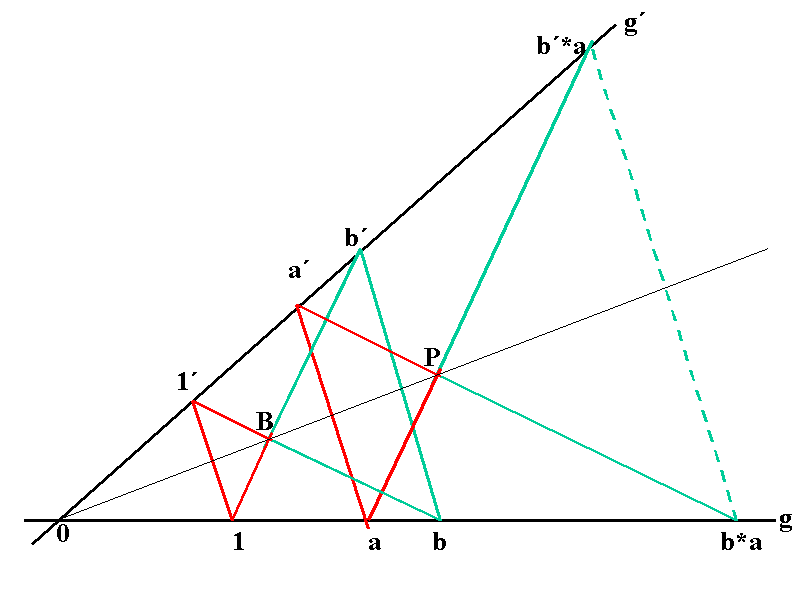
Aus "rot" mit (D^-1) folgt, dass 0, B, P kollinear sind.
Mit "grün" folgt:
(a´ * b´)(a * b)] || (bb´) || (aa´).
O.K.!

Zu 3)
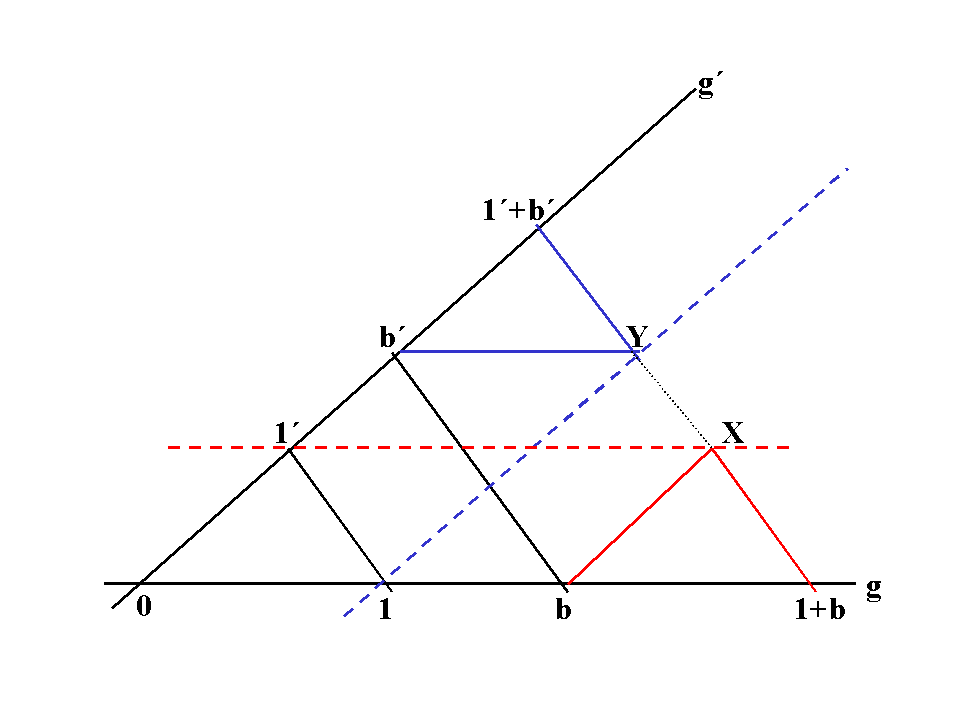
Es gilt: a + b = c.
Mit b = l * a folgt nach dem Distributivgesetz im Schiefkörper (1 + l) a = c.
Mit 4) gilt dann
(1 + l )p * a p = c p
= (1 p + l p) * a p
= 1 p a p + l p a p
= a p + (l a) p = a p + b p.
Deshalb reicht es den Spezialfall a = 1 zu zeigen.
O.K.!

- Þ Satz: (Es gelten nach den obigen Überlegungen folgende Voraussetzungen:
Es seien feste Punkte P, Q und
die Gerade g durch P, Q (mit P = 0, Q = 1) gegeben.
Für beliebige zulässige Tripel T_i = (A_i, B_i, R_i) existieren Parallelprojektionen p₁...p_k
mit A_ip₁...p_k = P_i und B_ip₁...p_k = Q_i und R_i´´ = R_ip₁...p_k, R_i´´ ÎK_{0, 1}.)
Für Tripel T₁ mit R₁´´ und T₂ mit R₂´´ ist T₁ ~ T₂ genau dann, wenn R₁´´ = R₂´´ (analog zu l) ist.

Beweis: "Þ": Hilfssatz.
"Ü": Selbst.

Überlegungen zur Definition 2 (siehe Übung):

a: A ® A ist eine affine Abbildung, wenn
1) a Î Koll (A);
2) T ~ Ta für alle T.

Lösung der Aufgabe 26a):

Beh.:
Für A = A (V) gilt:
T (V) * GL (V) = Aff (A) £ Koll (A) = T (V) * GL (V)
Beweis:
i): T (V) £ Aff (A) : Þ O.K.!
GL (V) £ Aff (A) : Þ O.K.!

ii) Es sei a Î Aff (A)£ Koll (A) = T (V) * GL (V)
Þ a = t * j, t Î T (V), j Î GL (V)
Untersuche j: j bildet ebenfalls T j ~ T ab. Also ist j Î Aff (A).
a = a * 1 Þ a * j = a * 1 j = a^g * 1 j mit g = 1, da j Î GL(V)
Þ j Î GL(V). [K4]

Frage: Wie lautet der Strahlensatz im axiomatischen Aufbau?

- Þ Satz: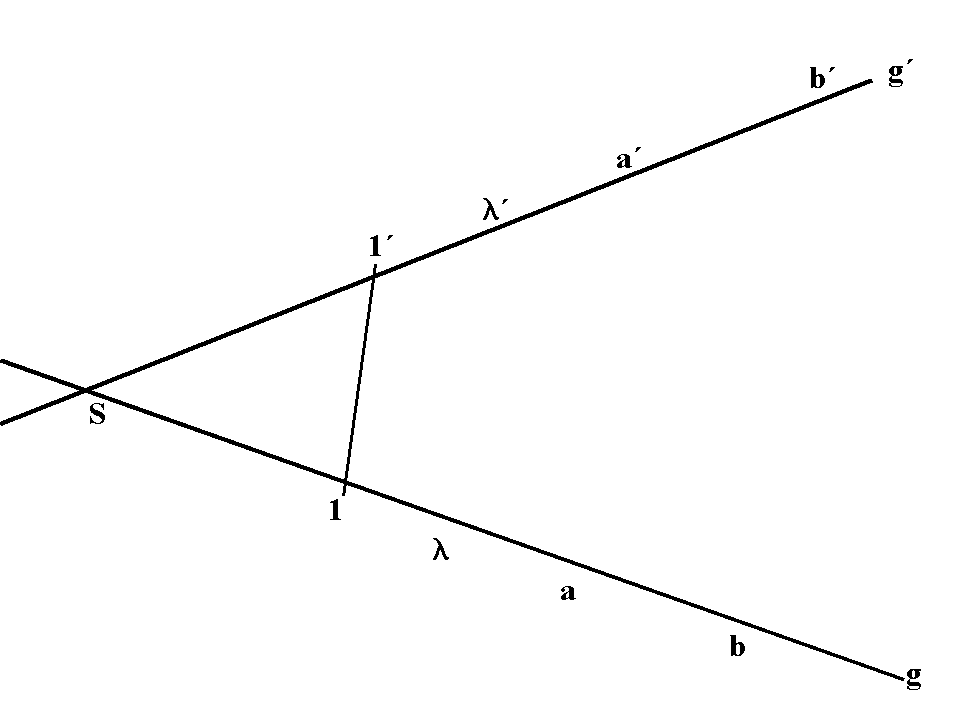 (Vor.: aa´ || 11´.)



Für beliebige l * a = b Î g
und l´ * a´ = b´Îg´ gilt:
bb´ || 11´ Û l l´ || 11´.
Beweis: : mit 4) O.K!

Kommentare

K1: Das geometrische Teilverhältnis von T als Element des Koordinatenkörpers wird am Ende des Kommentars [K4] eingeführt.
Zurück zur Quelle des Kommentars.

K2: Wo bin ich? Sicher brauchen wir einen affinen Raum im Sinne der Axiome. Der reicht auch aus, wenn wir statt Beträgen (in welchem Sinne?) von Vektoren viel sinnvoller die Vektoren selbst nehmen! Also neue
Definition: ATV(P, Q, R) = l, wenn PR^> = l PQ^> ist. Hier bezeichnet XY^> den Vektor von X nach Y.
Zurück zur Quelle des Kommentars.

K3: Siehe hierzu den Hilfssatz unter Kommentar K .
Zurück zur Quelle des Kommentars.

K4: Eine ausführliche und hoffentlich verständliche Lösung zu Aufgabe 26 finden Sie hier.
Zurück zur Quelle des Kommentars.