




Next: Kondensation
Up: Primzahl 11, Block 1
Previous: Primzahl 11, Block 1
Inhalt
Index
Der Brauerbaum
In Abbildung 3.1 ist der Brauerbaum von 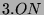 zur Primzahl 11 im Block 1 dargestellt. In der Tabelle
3.1 sind die Nummern und Charaktergrade der
entsprechenden gewöhnlichen Charaktere bzw.der Brauercharaktere des
ersten Blocks aufgelistet.
zur Primzahl 11 im Block 1 dargestellt. In der Tabelle
3.1 sind die Nummern und Charaktergrade der
entsprechenden gewöhnlichen Charaktere bzw.der Brauercharaktere des
ersten Blocks aufgelistet.
Abbildung 3.1:
Die Brauerbaum-Kandidaten von 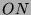 , Primzahl 11, Block 1
, Primzahl 11, Block 1
 |
Tabelle 3.1:
Nummern der Charaktere an den Knoten und Kanten
des Brauerbaums von 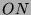 , Primzahl 11, Block 1
, Primzahl 11, Block 1
| Knoten-Nr. |
CAS-Nr. |
| (
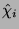 ) ) |
Grad |
| 1 |
1 |
| |
1 |
| 2 |
2 |
| |
10944 |
| 3 |
10 |
| |
37696 |
| 4 |
15 |
| |
58653 |
| 5 |
18 |
| |
85064 |
| 6 |
23 |
| |
175616 |
| 7 |
24 |
| |
175616 |
| 8 |
25 |
| |
175770 |
| 9 |
26 |
| |
207360 |
| 10 |
27 |
| |
207360 |
| 11 |
28 |
| |
207360 |
| Kanten-Nr. |
| (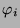 ) ) |
Grad |
| 1 |
| |
1 |
|---|
| 2 |
| |
10787 |
|---|
| 3 |
| |
10943 |
|---|
| 4 |
| |
26909 |
|---|
| 5 |
| |
31744 |
|---|
| 6 |
| |
42533 |
|---|
| 7 |
| |
74277 |
|---|
| 8 |
| |
133083 |
|---|
| 9 |
| |
164827 |
|---|
| 10 |
| |
175616 |
|---|
|
Es gibt zwei Bahnen algebraisch konjugierter Charaktere:
- 1.
- Die erste Bahn enthält die Charaktere
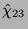 und
und
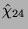 , dies sind die Knoten
, dies sind die Knoten
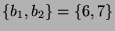 . Die
Charaktere
. Die
Charaktere
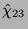 und
und
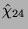 unterscheiden
sich nur auf den 15er-Klassen
unterscheiden
sich nur auf den 15er-Klassen 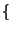 15A,
15B
15A,
15B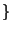 .
.
- 2.
- Die zweite Bahn enthält die Charaktere
 ,
,
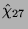 und
und
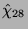 , dies sind die Knoten
, dies sind die Knoten
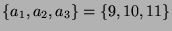 . Diese Charaktere unterscheiden
sich nur auf den 19er-Klassen
. Diese Charaktere unterscheiden
sich nur auf den 19er-Klassen  19A, 19B,
19C
19A, 19B,
19C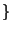 .
.
In [HL89] wurde oBdA.angenommen, daß
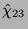 links von
links von
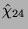 , sowie
, sowie
 links von
links von
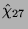 und
und
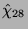 auf dem Brauerbaum
liegt. Diese Annahmen können hier nicht gemacht werden, da (in Abschnitt
2.3.2) Vertreter für die Konjugiertenklassen festgelegt
wurden. Werden die Vertreter der Konjugiertenklassen vertauscht, so
führt dies zu einer anderen Verteilung der Knoten am Brauerbaum. Dazu
siehe auch Abschnitt 3.1.3. Daher
bleiben
auf dem Brauerbaum
liegt. Diese Annahmen können hier nicht gemacht werden, da (in Abschnitt
2.3.2) Vertreter für die Konjugiertenklassen festgelegt
wurden. Werden die Vertreter der Konjugiertenklassen vertauscht, so
führt dies zu einer anderen Verteilung der Knoten am Brauerbaum. Dazu
siehe auch Abschnitt 3.1.3. Daher
bleiben
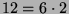 mögliche Brauerbaum-Kandidaten übrig, die zu
untersuchen sind.
mögliche Brauerbaum-Kandidaten übrig, die zu
untersuchen sind.





Next: Kondensation
Up: Primzahl 11, Block 1
Previous: Primzahl 11, Block 1
Inhalt
Index
Markus Ottensmann
2000-02-10
![]() zur Primzahl 11 im Block 1 dargestellt. In der Tabelle
3.1 sind die Nummern und Charaktergrade der
entsprechenden gewöhnlichen Charaktere bzw.der Brauercharaktere des
ersten Blocks aufgelistet.
zur Primzahl 11 im Block 1 dargestellt. In der Tabelle
3.1 sind die Nummern und Charaktergrade der
entsprechenden gewöhnlichen Charaktere bzw.der Brauercharaktere des
ersten Blocks aufgelistet.