




Next: Änderungen bei den Repräsentanten
Up: Primzahl 11, Block 1
Previous: Der Brauerbaum
Inhalt
Index
Kondensation
Sei
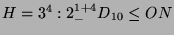 (die sechste
maximale Untergruppe von
(die sechste
maximale Untergruppe von 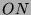 ) Kondensationsgruppe und betrachte die
Kondensation der Permutationsmoduln
) Kondensationsgruppe und betrachte die
Kondensation der Permutationsmoduln
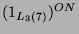 und
und
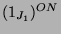 . Als Kondensationsalgebra nehme
. Als Kondensationsalgebra nehme
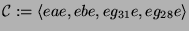 . In der
Tabelle 3.2 sind die Zerlegungszahlen des ersten
Blocks für diese Permutationsmoduln und in der Tabelle
3.3 sind die Dimensionen der einfachen kondensierten
. In der
Tabelle 3.2 sind die Zerlegungszahlen des ersten
Blocks für diese Permutationsmoduln und in der Tabelle
3.3 sind die Dimensionen der einfachen kondensierten
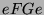 -Moduln des ersten Blocks angegeben. Die Dimension des
kondensierten Permutationsmoduls
-Moduln des ersten Blocks angegeben. Die Dimension des
kondensierten Permutationsmoduls
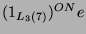 ist 16 und die
Dimension des kondensierten Permutationsmoduls
ist 16 und die
Dimension des kondensierten Permutationsmoduls
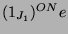 ist
114.
ist
114.
Tabelle 3.2:
Zerlegungszahlen (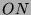 , Primzahl 11, Block 1)
, Primzahl 11, Block 1)
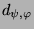 |
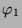 |
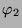 |
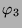 |
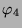 |
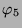 |
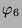 |
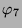 |
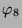 |
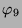 |
 |
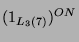 |
2 |
2 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
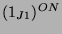 |
2 |
1 |
3 |
2 |
2 |
2 |
1 |
2 |
3 |
2 |
|
Tabelle 3.3:
Skalarprodukte (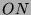 , Primzahl 11, Block 1)
, Primzahl 11, Block 1)
|
|
Beim Kondensieren der Moduln
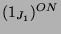 und
und
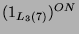 mit
mit 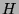 ergeben sich für die kondensierten Elemente
ergeben sich für die kondensierten Elemente  und
und
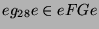 die Spuren auf den Konstituenten der kondensierten
Permutationsmoduln entsprechend den Tabellen 3.5
und 3.6. In den Tabellen
3.7 bzw.3.8 sind
die Werte
die Spuren auf den Konstituenten der kondensierten
Permutationsmoduln entsprechend den Tabellen 3.5
und 3.6. In den Tabellen
3.7 bzw.3.8 sind
die Werte
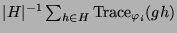 der
Spurformel (2.3) für die verschiedenen
Brauerbaum-Kandidaten für die Elemente
der
Spurformel (2.3) für die verschiedenen
Brauerbaum-Kandidaten für die Elemente  , bzw.
, bzw. enthalten.
enthalten.
Tabelle 3.5:
Spuren der kondensierten Elemente  und
und
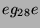 auf den Konstituenten von
auf den Konstituenten von
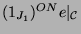 ,
(
,
( Primzahl 11, Block 1).
Primzahl 11, Block 1).
| Name |
Anzahl |
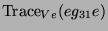 |
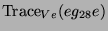 |
| 1a |
2 |
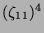 |
0 |
| 1b |
2 |
 |
 |
| 2a |
2 |
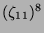 |
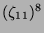 |
| 2b |
2 |
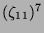 |
 |
| 2c |
2 |
 |
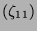 |
| 3a |
1 |
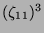 |
0 |
| 3b |
1 |
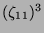 |
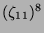 |
| 3c |
1 |
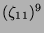 |
0 |
| 3d |
1 |
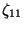 |
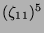 |
| 4a |
2 |
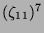 |
 |
| 4b |
2 |
 |
 |
| 4c |
1 |
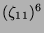 |
 |
| 5a |
1 |
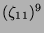 |
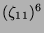 |
| 6a |
2 |
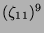 |
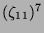 |
| 6b |
3 |
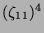 |
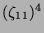 |
| 7a |
1 |
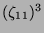 |
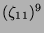 |
| 12a1 |
2 |
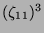 |
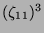 |
|
Tabelle 3.6:
Spuren der kondensierten Elemente  und
und
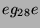 auf den Konstituenten von
auf den Konstituenten von
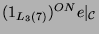 ,
(
,
(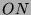 Primzahl 11, Block 1).
Primzahl 11, Block 1).
| Name |
Anzahl |
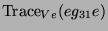 |
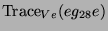 |
| 1a |
1 |
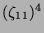 |
0 |
| 1b |
2 |
 |
 |
| 2a |
1 |
 |
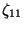 |
| 3a |
1 |
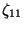 |
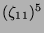 |
| 4a |
1 |
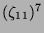 |
 |
| 4b |
1 |
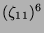 |
 |
|
Tabelle 3.7:
Spurformel für  für die verschiedenen
Brauercharakter-Kandidaten von
für die verschiedenen
Brauercharakter-Kandidaten von 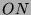 , Primzahl 11, Block 1
, Primzahl 11, Block 1
| |
|
|
|
|
 |
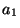 |
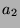 |
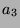 |
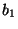 |
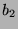 |
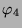 |
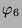 |
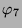 |
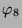 |
| 9 |
10 |
11 |
6 |
7 |
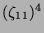 |
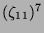 |
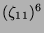 |
 |
| 9 |
10 |
11 |
7 |
6 |
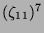 |
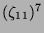 |
0 |
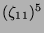 |
| 9 |
11 |
10 |
6 |
7 |
 |
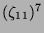 |
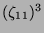 |
 |
| 9 |
11 |
10 |
7 |
6 |
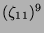 |
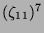 |
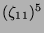 |
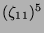 |
| 10 |
9 |
11 |
6 |
7 |
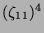 |
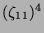 |
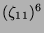 |
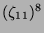 |
| 10 |
9 |
11 |
7 |
6 |
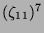 |
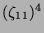 |
0 |
 |
| 10 |
11 |
9 |
6 |
7 |
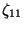 |
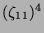 |
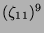 |
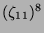 |
| 10 |
11 |
9 |
7 |
6 |
 |
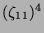 |
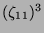 |
 |
| 11 |
9 |
10 |
6 |
7 |
 |
 |
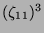 |
 |
| 11 |
9 |
10 |
7 |
6 |
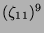 |
 |
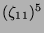 |
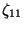 |
| 11 |
10 |
9 |
6 |
7 |
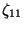 |
 |
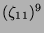 |
 |
| 11 |
10 |
9 |
7 |
6 |
 |
 |
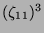 |
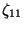 |
|
Tabelle 3.8:
Spurformel für  für die verschiedenen
Brauercharakter-Kandidaten von
für die verschiedenen
Brauercharakter-Kandidaten von 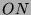 , Primzahl 11, Block 1
, Primzahl 11, Block 1
| |
|
|
|
|
 |
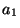 |
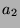 |
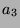 |
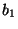 |
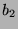 |
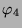 |
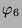 |
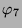 |
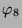 |
| 9 |
10 |
11 |
6 |
7 |
0 |
 |
 |
 |
| 9 |
10 |
11 |
7 |
6 |
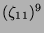 |
 |
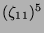 |
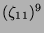 |
| 9 |
11 |
10 |
6 |
7 |
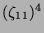 |
 |
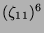 |
 |
| 9 |
11 |
10 |
7 |
6 |
0 |
 |
 |
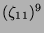 |
| 10 |
9 |
11 |
6 |
7 |
0 |
0 |
 |
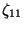 |
| 10 |
9 |
11 |
7 |
6 |
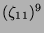 |
0 |
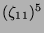 |
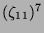 |
| 10 |
11 |
9 |
6 |
7 |
 |
0 |
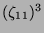 |
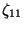 |
| 10 |
11 |
9 |
7 |
6 |
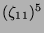 |
0 |
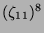 |
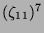 |
| 11 |
9 |
10 |
6 |
7 |
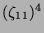 |
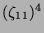 |
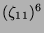 |
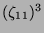 |
| 11 |
9 |
10 |
7 |
6 |
0 |
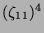 |
 |
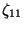 |
| 11 |
10 |
9 |
6 |
7 |
 |
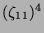 |
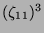 |
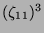 |
| 11 |
10 |
9 |
7 |
6 |
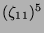 |
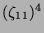 |
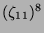 |
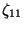 |
|
Nun werden die Einzelteile zusammengefügt, indem die verschiedenen
Spuren, die für die einzelnen Fälle berechneten wurden, nach der
Spurformel (2.3) miteinander verglichen werden. Dazu
betrachte die Spuren für das Element  :
:
Insgesamt folgt somit 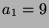 ,
, 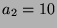 ,
, 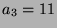 ,
, 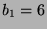 und
und
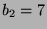 . Der Brauerbaum ist in Abbildung 3.2
dargestellt.
. Der Brauerbaum ist in Abbildung 3.2
dargestellt.
Abbildung 3.2:
Der Brauerbaum von 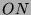 , Primzahl 11, Block 1
, Primzahl 11, Block 1
![\begin{figure}
\begin{center}
\setlength{\unitlength}{1mm} \begin{picture}
(11...
...akebox(0,0)[t]{\footnotesize\textsf{10}}}
\end{picture} \end{center}\end{figure}](img758.png) |





Next: Änderungen bei den Repräsentanten
Up: Primzahl 11, Block 1
Previous: Der Brauerbaum
Inhalt
Index
Markus Ottensmann
2000-02-10
![]() (die sechste
maximale Untergruppe von
(die sechste
maximale Untergruppe von ![]() ) Kondensationsgruppe und betrachte die
Kondensation der Permutationsmoduln
) Kondensationsgruppe und betrachte die
Kondensation der Permutationsmoduln
![]() und
und
![]() . Als Kondensationsalgebra nehme
. Als Kondensationsalgebra nehme
![]() . In der
Tabelle 3.2 sind die Zerlegungszahlen des ersten
Blocks für diese Permutationsmoduln und in der Tabelle
3.3 sind die Dimensionen der einfachen kondensierten
. In der
Tabelle 3.2 sind die Zerlegungszahlen des ersten
Blocks für diese Permutationsmoduln und in der Tabelle
3.3 sind die Dimensionen der einfachen kondensierten
![]() -Moduln des ersten Blocks angegeben. Die Dimension des
kondensierten Permutationsmoduls
-Moduln des ersten Blocks angegeben. Die Dimension des
kondensierten Permutationsmoduls
![]() ist 16 und die
Dimension des kondensierten Permutationsmoduls
ist 16 und die
Dimension des kondensierten Permutationsmoduls
![]() ist
114.
ist
114.
![]() und
und
![]() mit
mit ![]() ergeben sich für die kondensierten Elemente
ergeben sich für die kondensierten Elemente ![]() und
und
![]() die Spuren auf den Konstituenten der kondensierten
Permutationsmoduln entsprechend den Tabellen 3.5
und 3.6. In den Tabellen
3.7 bzw.3.8 sind
die Werte
die Spuren auf den Konstituenten der kondensierten
Permutationsmoduln entsprechend den Tabellen 3.5
und 3.6. In den Tabellen
3.7 bzw.3.8 sind
die Werte
![]() der
Spurformel (2.3) für die verschiedenen
Brauerbaum-Kandidaten für die Elemente
der
Spurformel (2.3) für die verschiedenen
Brauerbaum-Kandidaten für die Elemente ![]() , bzw.
, bzw.![]() enthalten.
enthalten.
![]() :
: