




Next: Repräsentanten von Konjugiertenklassen in
Up: Spuren im Schnee
Previous: Spuren
Inhalt
Index
Schnee
Ein schwieriges Problem ist es, Schneeflocken zu zählen, die vom
Himmel fallen. Da ist es leichter, die Nebenklassenverteilung
 für
für
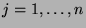 bei gegebenem
bei gegebenem 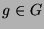 und
und 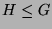 zu bestimmen. Dazu laufe (mit ,,brutaler Gewalt``) mit
zu bestimmen. Dazu laufe (mit ,,brutaler Gewalt``) mit 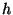 durch
die ganze Untergruppe
durch
die ganze Untergruppe 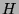 und bestimme die Zugehörigkeit des
Elementes
und bestimme die Zugehörigkeit des
Elementes 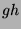 zu einer Konjugiertenklasse
zu einer Konjugiertenklasse 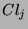 von
von 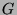 durch
genügend viele Invarianten einer Konjugiertenklasse:
durch
genügend viele Invarianten einer Konjugiertenklasse:
- 1.
- Die Ordnung des Elementes
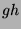 bestimmt die Menge der
Konjugiertenklassen, in denen
bestimmt die Menge der
Konjugiertenklassen, in denen 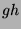 liegen kann. Falls es nur eine
Konjugiertenklasse dieser Ordnung gibt, so wird die Zugehörigkeit
zu der Konjugiertenklasse schon durch die Elementordnung
festgelegt.
liegen kann. Falls es nur eine
Konjugiertenklasse dieser Ordnung gibt, so wird die Zugehörigkeit
zu der Konjugiertenklasse schon durch die Elementordnung
festgelegt.
- 2.
- Das Element
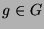 und die Erzeuger von
und die Erzeuger von 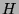 sind als Wörter
in Standarderzeugern von
sind als Wörter
in Standarderzeugern von 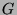 gegeben. Ist auch
gegeben. Ist auch 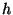 als Wort in den
Erzeugern von
als Wort in den
Erzeugern von 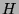 gegeben, so kann das Element
gegeben, so kann das Element 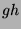 als Wort in den
Standarderzeugern von
als Wort in den
Standarderzeugern von 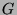 geschrieben werden. Dann kann man das Wort
von
geschrieben werden. Dann kann man das Wort
von 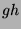 in genügend vielen geeigneten Darstellungen berechnen, die
zugehörigen Spuren bestimmen und mit den bekannten Werten der
Charaktertafel vergleichen. Dazu eignet sich z.B.eine
Permutationsdarstellung oder eine Matrixdarstellung von kleinem
Grad, schließlich müssen die Elemente, die als Worte in
Standarderzeugern gegeben sind, explizit durch
Matrixmultiplikationen berechnet werden. Um Spuren zu vergleichen,
müssen natürlich auch Repräsentanten von den Konjugiertenklassen
bekannt sein.
in genügend vielen geeigneten Darstellungen berechnen, die
zugehörigen Spuren bestimmen und mit den bekannten Werten der
Charaktertafel vergleichen. Dazu eignet sich z.B.eine
Permutationsdarstellung oder eine Matrixdarstellung von kleinem
Grad, schließlich müssen die Elemente, die als Worte in
Standarderzeugern gegeben sind, explizit durch
Matrixmultiplikationen berechnet werden. Um Spuren zu vergleichen,
müssen natürlich auch Repräsentanten von den Konjugiertenklassen
bekannt sein.
Die kleinste Permutationsdarstellung von
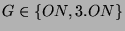 ist die
durch
ist die
durch  induzierte Operation auf den Nebenklassen von
induzierte Operation auf den Nebenklassen von 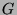 nach
nach
 . Für
. Für 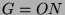 ist dies eine Operation auf 122
ist dies eine Operation auf 122 760
Punkten und für
760
Punkten und für  ist dies eine Operation auf 368
ist dies eine Operation auf 368 280
Punkten. Daher will man nicht alle Elemente gleichzeitig
aufschreiben. Um die Elemente
280
Punkten. Daher will man nicht alle Elemente gleichzeitig
aufschreiben. Um die Elemente 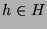 als Worte in den Erzeugern von
als Worte in den Erzeugern von
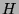 zu erhalten, benutzte ich einen Bahnenalgorithmus mit Tiefensuche,
um nacheinander alle Elemente
zu erhalten, benutzte ich einen Bahnenalgorithmus mit Tiefensuche,
um nacheinander alle Elemente 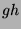 für
für
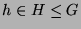 zu bestimmen.
zu bestimmen.





Next: Repräsentanten von Konjugiertenklassen in
Up: Spuren im Schnee
Previous: Spuren
Inhalt
Index
Markus Ottensmann
2000-02-10
![]() für
für
![]() bei gegebenem
bei gegebenem ![]() und
und ![]() zu bestimmen. Dazu laufe (mit ,,brutaler Gewalt``) mit
zu bestimmen. Dazu laufe (mit ,,brutaler Gewalt``) mit ![]() durch
die ganze Untergruppe
durch
die ganze Untergruppe ![]() und bestimme die Zugehörigkeit des
Elementes
und bestimme die Zugehörigkeit des
Elementes ![]() zu einer Konjugiertenklasse
zu einer Konjugiertenklasse ![]() von
von ![]() durch
genügend viele Invarianten einer Konjugiertenklasse:
durch
genügend viele Invarianten einer Konjugiertenklasse: