




Next: Restlicher Beweis zur Rekonstruktion
Up: Primzahl 11, Block 1
Previous: Änderungen bei den Repräsentanten
Inhalt
Index
Rekonstruktion des Brauerbaums
In Tabelle 3.9 sind vier projektive
Charaktere
 und deren Zerlegung in die
irreduziblen gewöhnlichen Charaktere des ersten Blocks angegeben. Die
Tabelle ist aus [HL89] entnommen. Aus diesen projektiven
Charakteren können die Brauerbaum-Kandidaten rekonstruiert werden:
und deren Zerlegung in die
irreduziblen gewöhnlichen Charaktere des ersten Blocks angegeben. Die
Tabelle ist aus [HL89] entnommen. Aus diesen projektiven
Charakteren können die Brauerbaum-Kandidaten rekonstruiert werden:
Tabelle 3.9:
Projektive Charaktere von  , Primzahl 11, Block 1
, Primzahl 11, Block 1
| Nr.: |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| Typ: |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
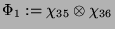 |
1 |
1 |
|
|
|
|
|
|
|
|
|
 |
|
1 |
|
|
|
|
|
1 |
|
|
|
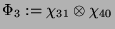 |
|
|
|
|
1 |
1 |
1 |
|
1 |
1 |
1 |
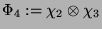 |
|
5 |
11 |
18 |
26 |
56 |
56 |
58 |
66 |
66 |
66 |
|
Man sieht (z.B.nach [CCN$^$85]), daß alle irreduziblen
gewöhnlichen Charaktere des ersten Blocks reelle Charakterwerte
habe. Nach Satz 1.3.3 ist der Brauerbaum also eine gerade
Linie.
Mit 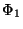 folgt, daß die Knoten 1 und 2 Nachbarn sind. Mit
folgt, daß die Knoten 1 und 2 Nachbarn sind. Mit
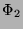 folgt, daß 2 und 8 benachbart sind. Mit
(1.4) für
folgt, daß 2 und 8 benachbart sind. Mit
(1.4) für
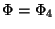 und
und
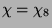 folgt, daß 8 und
folgt, daß 8 und 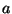 für
für
 benachbart sind. Dies ergibt bis jetzt den folgenden Teilbaum:
benachbart sind. Dies ergibt bis jetzt den folgenden Teilbaum:
![\begin{picture}
(40,10)
\put(5,1){\line(1,0){30}}
\multiput(5,1)(10,0){4}{\cir...
...35,3){\makebox(0,0)[b]{$a$}}
\put(36,1){\makebox(0,0)[lb]{\dots}}
\end{picture}](img776.png)
Der durch
definierte Charakter ist nach (1.6)
wieder ein projektiver Charakter.
| Nr.: |
1 |
2 |
3 |
4 |
5 |
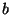 |
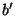 |
8 |
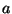 |
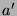 |
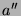 |
| Typ: |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
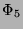 |
|
|
11 |
18 |
26 |
56 |
56 |
|
13 |
66 |
66 |
Da der Nachbar von Knoten 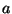 vom Typ
vom Typ  sein muß, gibt es die
drei Möglichkeiten 4, 5 und
sein muß, gibt es die
drei Möglichkeiten 4, 5 und 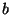 mit
mit
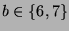 .
.
- 1.
- 4 kann nicht zu
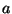 benachbart sein, da
benachbart sein, da
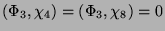 aber
aber
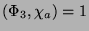 für alle
für alle
 . Dies ist ein Widerspruch zu
(1.4).
. Dies ist ein Widerspruch zu
(1.4).
- 2.
- Betrachte den Fall, daß 5 benachbart zu
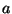 ist. Es gilt
ist. Es gilt
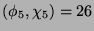 . Mit
. Mit 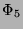 und
(1.4), folgt dann, daß der
andere Nachbar von 5 ein
und
(1.4), folgt dann, daß der
andere Nachbar von 5 ein 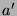 mit
mit
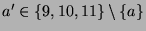 ist, da 3 der einzige andere Knoten vom Typ
ist, da 3 der einzige andere Knoten vom Typ  ist,
aber
ist,
aber
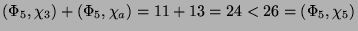 . Ebenso folgt, daß dann
. Ebenso folgt, daß dann 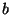 mit
mit
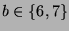 der andere Nachbar von
der andere Nachbar von 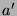 ist, den bisherigen
Informationen folgt, daß der Baum die folgenden Form hat:
Nach (1.6) ist
ein projektiver Charakter.
ist, den bisherigen
Informationen folgt, daß der Baum die folgenden Form hat:
Nach (1.6) ist
ein projektiver Charakter.
| Nr.: |
1 |
2 |
3 |
4 |
5 |
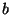 |
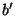 |
8 |
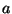 |
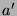 |
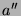 |
| Typ: |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
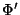 |
|
|
11 |
18 |
|
3 |
56 |
|
|
|
66 |
Mit 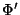 und (1.4) läßt sich
nun ausschließen, daß
und (1.4) läßt sich
nun ausschließen, daß 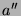 Nachbar von
Nachbar von 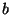 ist. Also ist
ist. Also ist 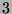 Nachbar von
Nachbar von 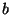 . Als Nachbar der 3 kann nun entweder der Knoten 4
oder der Knoten
. Als Nachbar der 3 kann nun entweder der Knoten 4
oder der Knoten 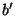 mit
mit
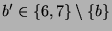 sein.
sein.
- Der Fall, daß Knoten 4 Nachbar von 3 ist liefert dann
sofort mit
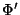 den Brauerbaum-Kandidaten:
den Brauerbaum-Kandidaten:
- Der Fall, daß Knoten
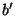 Nachbar von 3 ist liefert sofort
mit
Nachbar von 3 ist liefert sofort
mit 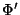 den Brauerbaum-Kandidaten:
den Brauerbaum-Kandidaten:
Diese beiden Kandidaten können mit den vorhandenen projektiven
Charakteren nicht ausgeschlossen werden.
- 3.
- Betrachte nun den Fall, daß
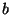 mit
mit
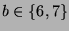 Nachbar von
Nachbar von
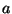 ist. Mit
ist. Mit 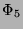 und (1.4)
folgt dann sofort, daß
und (1.4)
folgt dann sofort, daß 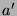 mit
mit
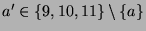 Nachbar von
Nachbar von 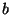 ist:
Nach (1.6) ist
ein projektiver Charakter.
ist:
Nach (1.6) ist
ein projektiver Charakter.
| Nr.: |
1 |
2 |
3 |
4 |
5 |
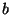 |
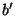 |
8 |
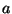 |
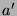 |
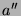 |
| Typ: |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
11 |
18 |
26 |
|
56 |
|
|
23 |
66 |
Als Nachbar von Knoten 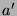 kommen zunächst die Knoten 5 und
kommen zunächst die Knoten 5 und 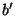 mit
mit
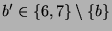 in Frage.
in Frage.
Angenommen 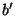 Nachbar ist Nachbar von
Nachbar ist Nachbar von 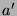 . Nach
(1.6) ist dann
. Nach
(1.6) ist dann
ein projektiver Charakter, gilt
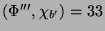 und damit kommt nur
und damit kommt nur 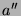 mit
mit
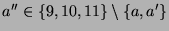 als Nachbar von
als Nachbar von 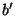 in Frage. Aber es gilt nun
was ein Widerspruch zu (1.4) ist.
in Frage. Aber es gilt nun
was ein Widerspruch zu (1.4) ist.
Somit folgt, daß 5 benachbart zu 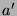 ist. Mit
(1.6) bleibt
ist. Mit
(1.6) bleibt 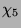 mit
Vielfachheit 3 zurück. Zunächst kommen die Knoten
mit
Vielfachheit 3 zurück. Zunächst kommen die Knoten 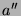 und
und 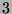 als Nachbarn von
als Nachbarn von 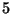 in Frage. Der Knoten
in Frage. Der Knoten 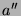 läßt sich als
Nachbar von
läßt sich als
Nachbar von 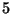 aber wie oben ausschließen. Also ergibt sich der
folgende Baum:
aber wie oben ausschließen. Also ergibt sich der
folgende Baum:
Nach (1.6) ist
ein projektiver Charakter.
| Nr.: |
1 |
2 |
3 |
4 |
5 |
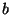 |
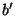 |
8 |
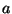 |
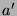 |
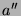 |
| Typ: |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
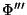 |
|
|
8 |
18 |
|
|
56 |
|
|
|
66 |
Der Nachbar von 3 kann nun der Knoten 4 oder der Knoten 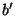 sein.
sein.
- Der Fall, daß 4 der Nachbar von Knoten 3 ist, liefert den
Brauerbaum-Kandidaten
- Der Fall, daß
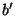 der Nachbar von Knoten 3 ist, liefert den
Brauerbaum-Kandidaten
der Nachbar von Knoten 3 ist, liefert den
Brauerbaum-Kandidaten
Auch diese beiden Kandidaten können mit den vorhandenen
projektiven Charakteren nicht ausgeschlossen werden.
Insgesamt bleiben die folgenden vier Kandidaten übrig, die mit allen
angegebenen projektiven Charakteren konsistent sind:
In [HL89] werden die Kandidaten
(3.1), (3.3) und
(3.4) mit Hilfe der Green-Korrespondenz
ausgeschlossen. In Abschnitt
3.1.5 zeige ich unabhängig
von der Green-Korrespondenz allein mit Hilfe der Kondensation von
Permutationsmoduln, daß diese Kandidaten falsch sind.





Next: Restlicher Beweis zur Rekonstruktion
Up: Primzahl 11, Block 1
Previous: Änderungen bei den Repräsentanten
Inhalt
Index
Markus Ottensmann
2000-02-10
![]() und deren Zerlegung in die
irreduziblen gewöhnlichen Charaktere des ersten Blocks angegeben. Die
Tabelle ist aus [HL89] entnommen. Aus diesen projektiven
Charakteren können die Brauerbaum-Kandidaten rekonstruiert werden:
und deren Zerlegung in die
irreduziblen gewöhnlichen Charaktere des ersten Blocks angegeben. Die
Tabelle ist aus [HL89] entnommen. Aus diesen projektiven
Charakteren können die Brauerbaum-Kandidaten rekonstruiert werden:
![]() folgt, daß die Knoten 1 und 2 Nachbarn sind. Mit
folgt, daß die Knoten 1 und 2 Nachbarn sind. Mit
![]() folgt, daß 2 und 8 benachbart sind. Mit
(1.4) für
folgt, daß 2 und 8 benachbart sind. Mit
(1.4) für
![]() und
und
![]() folgt, daß 8 und
folgt, daß 8 und ![]() für
für
![]() benachbart sind. Dies ergibt bis jetzt den folgenden Teilbaum:
benachbart sind. Dies ergibt bis jetzt den folgenden Teilbaum:
![]()
![]() Nachbar ist Nachbar von
Nachbar ist Nachbar von ![]() . Nach
(1.6) ist dann
. Nach
(1.6) ist dann
![]() ist. Mit
(1.6) bleibt
ist. Mit
(1.6) bleibt ![]() mit
Vielfachheit 3 zurück. Zunächst kommen die Knoten
mit
Vielfachheit 3 zurück. Zunächst kommen die Knoten ![]() und
und ![]() als Nachbarn von
als Nachbarn von ![]() in Frage. Der Knoten
in Frage. Der Knoten ![]() läßt sich als
Nachbar von
läßt sich als
Nachbar von ![]() aber wie oben ausschließen. Also ergibt sich der
folgende Baum:
aber wie oben ausschließen. Also ergibt sich der
folgende Baum: