




Next: Primzahl 11, Block 2
Up: Primzahl 11, Block 1
Previous: Rekonstruktion des Brauerbaums
Inhalt
Index
Restlicher Beweis zur Rekonstruktion des Brauerbaums
In diesem Abschnitt wird gezeigt, daß die Brauerbaum-Kandidaten
(3.1), (3.3) und
(3.4), die in [HL89] mit Hilfe der
Green-Korrespondenz ausgeschlossen wurden, einen Widerspruch liefern,
wenn man die in 3.1.2 konstruierten
kondensierten Permutationsmoduln mit den Brauerbaum-Kandidaten
vergleicht.
Sei
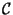 die in Abschnitt 3.1.2
benutzte Kondensationsalgebra. Dann betrachte den Permutationsmodul
die in Abschnitt 3.1.2
benutzte Kondensationsalgebra. Dann betrachte den Permutationsmodul
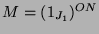 und berechne die Zerlegung des
kondensierten
und berechne die Zerlegung des
kondensierten
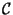 -Moduls
-Moduls
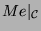 in seine
Konstituenten
in seine
Konstituenten 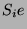 mit dem MeatAxe-Programm
chop:
mit dem MeatAxe-Programm
chop:
Die Dimensionen und die Vielfachheiten 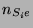 der
der
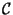 -Moduln
-Moduln 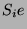 sind in der Tabelle
3.5 zu sehen.
sind in der Tabelle
3.5 zu sehen.
Desweiteren berechne mit GAP für jeden Brauerbaum-Kandidaten
die zugehörigen Brauercharakter-Kandidaten des ersten Blocks
 . Aus diesen Kandidaten kann man die
Zerlegungszahlen und mit dem Skalarprodukt die Dimension der einfachen
. Aus diesen Kandidaten kann man die
Zerlegungszahlen und mit dem Skalarprodukt die Dimension der einfachen
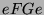 -Moduln berechnen. Es fällt auf, daß sich Dimension und
Vielfachheiten der einfachen
-Moduln berechnen. Es fällt auf, daß sich Dimension und
Vielfachheiten der einfachen 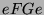 -Moduln für die verschiedenen
Brauerbaum-Kandidaten unterscheiden.
-Moduln für die verschiedenen
Brauerbaum-Kandidaten unterscheiden.
Da der
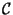 -Modul
-Modul
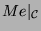 explizit konstruiert
wurde, ist bekannt, welche Zerlegung für die Kondensationsalgebra
explizit konstruiert
wurde, ist bekannt, welche Zerlegung für die Kondensationsalgebra
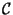 stimmt. Mit Bemerkung 2.1.2
werden nun die falschen Kandidaten ausgeschlossen.
stimmt. Mit Bemerkung 2.1.2
werden nun die falschen Kandidaten ausgeschlossen.
In der Tabelle 3.10 sind die Vielfachheiten der
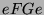 -Konstituenten von
-Konstituenten von 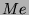 , sortiert nach ihrer Dimension
für die vier Brauerbaum-Kandidaten
(3.1), (3.2),
(3.3) und (3.4)
angegeben.
, sortiert nach ihrer Dimension
für die vier Brauerbaum-Kandidaten
(3.1), (3.2),
(3.3) und (3.4)
angegeben.
- Die Vielfachheiten und Dimensionen der Konstituenten von
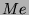 für den Kandidaten (3.2) stimmen mit den
berechneten Vielfachheiten
für den Kandidaten (3.2) stimmen mit den
berechneten Vielfachheiten 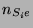 und Dimensionen
und Dimensionen
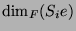 der Konstituenten von
der Konstituenten von
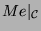 überein.
überein.
- Die Gesamtzahl der Konstituenten von
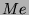 für den Kandidaten
(3.1) stimmt mit der Anzahl der
Konstituenten von
für den Kandidaten
(3.1) stimmt mit der Anzahl der
Konstituenten von
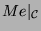 überein. Also spalten keine
Konstituenten von
überein. Also spalten keine
Konstituenten von 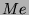 auf. Ein Vergleich der Dimensionen führt nun
zum Widerspruch.
auf. Ein Vergleich der Dimensionen führt nun
zum Widerspruch.
- Die Gesamtzahl der Konstituenten von
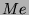 im Fall der Kandidaten
(3.3) und (3.4) ist
im Fall der Kandidaten
(3.3) und (3.4) ist
 . Wäre einer dieser Kandidaten richtig, so würde genau ein
Konstituent von
. Wäre einer dieser Kandidaten richtig, so würde genau ein
Konstituent von 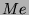 über der Kondensationsalgebra
über der Kondensationsalgebra
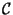 aufspalten. Ein Vergleich der Dimensionen führt aber zum
Widerspruch.
aufspalten. Ein Vergleich der Dimensionen führt aber zum
Widerspruch.
Somit folgt, daß die Brauerbaum-Kandidaten
(3.1), (3.3) und
(3.4) einen Widerspruch zu dem explizit
konstruierten
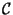 -Modul
-Modul
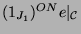 liefern.
liefern.
Tabelle 3.10:
Vielfachheiten der Konstituenten von
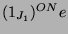 ,
sortiert nach Dimensionen für die verschiedenen
Brauerbaum-Kandidaten
(
,
sortiert nach Dimensionen für die verschiedenen
Brauerbaum-Kandidaten
(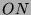 , Primzahl 11, Block 1)
, Primzahl 11, Block 1)
 |
Vielfachheiten der Konstituenten |
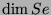 |
 |
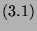 |
 |
 |
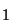 |
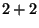 |
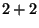 |
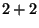 |
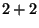 |
| 2 |
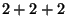 |
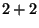 |
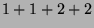 |
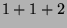 |
| 3 |
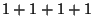 |
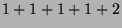 |
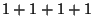 |
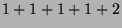 |
| 4 |
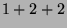 |
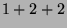 |
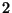 |
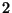 |
| 5 |
 |
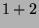 |
 |
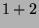 |
| 6 |
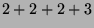 |
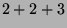 |
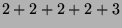 |
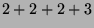 |
| 7 |
 |
 |
 |
 |
| Summe |
30 |
30 |
29 |
29 |
|





Next: Primzahl 11, Block 2
Up: Primzahl 11, Block 1
Previous: Rekonstruktion des Brauerbaums
Inhalt
Index
Markus Ottensmann
2000-02-10
![]() die in Abschnitt 3.1.2
benutzte Kondensationsalgebra. Dann betrachte den Permutationsmodul
die in Abschnitt 3.1.2
benutzte Kondensationsalgebra. Dann betrachte den Permutationsmodul
![]() und berechne die Zerlegung des
kondensierten
und berechne die Zerlegung des
kondensierten
![]() -Moduls
-Moduls
![]() in seine
Konstituenten
in seine
Konstituenten ![]() mit dem MeatAxe-Programm
chop:
mit dem MeatAxe-Programm
chop:
![]() . Aus diesen Kandidaten kann man die
Zerlegungszahlen und mit dem Skalarprodukt die Dimension der einfachen
. Aus diesen Kandidaten kann man die
Zerlegungszahlen und mit dem Skalarprodukt die Dimension der einfachen
![]() -Moduln berechnen. Es fällt auf, daß sich Dimension und
Vielfachheiten der einfachen
-Moduln berechnen. Es fällt auf, daß sich Dimension und
Vielfachheiten der einfachen ![]() -Moduln für die verschiedenen
Brauerbaum-Kandidaten unterscheiden.
-Moduln für die verschiedenen
Brauerbaum-Kandidaten unterscheiden.
![]() -Modul
-Modul
![]() explizit konstruiert
wurde, ist bekannt, welche Zerlegung für die Kondensationsalgebra
explizit konstruiert
wurde, ist bekannt, welche Zerlegung für die Kondensationsalgebra
![]() stimmt. Mit Bemerkung 2.1.2
werden nun die falschen Kandidaten ausgeschlossen.
stimmt. Mit Bemerkung 2.1.2
werden nun die falschen Kandidaten ausgeschlossen.
![]() -Konstituenten von
-Konstituenten von ![]() , sortiert nach ihrer Dimension
für die vier Brauerbaum-Kandidaten
(3.1), (3.2),
(3.3) und (3.4)
angegeben.
, sortiert nach ihrer Dimension
für die vier Brauerbaum-Kandidaten
(3.1), (3.2),
(3.3) und (3.4)
angegeben.