




Next: Restlicher Beweis zur Rekonstruktion
Up: Primzahl 19, Block 1
Previous: Kondensation
Inhalt
Index
Rekonstruktion des Brauerbaums
In Tabelle 3.24 sind drei projektive
Charaktere und deren Zerlegung in die irreduziblen gewöhnlichen
Charaktere des ersten Blocks angegeben. Die Tabelle ist aus
[HL89] entnommen. Aus diesen projektiven Charakteren kann
der Brauerbaum folgendermaßen rekonstruiert werden:
Tabelle 3.24:
Projektive Charaktere von 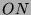 , Primzahl 19, Block 1
, Primzahl 19, Block 1
| Nr.: |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| Typ: |
 |
 |
 |
 |
 |
 |
 |
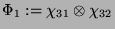 |
1 |
|
1 |
|
|
|
|
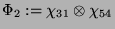 |
|
2 |
3 |
4 |
4 |
4 |
5 |
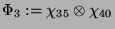 |
|
|
1 |
1 |
1 |
2 |
1 |
|
Man sieht (z.B.nach [CCN$^$85]), daß alle irreduziblen
gewöhnlichen Charaktere des ersten Blocks reelle Charakterwerte
habe. Nach Satz 1.3.3 ist der Brauerbaum also eine gerade
Linie.
Mit 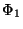 folgt, daß 1 und 3 benachbart sind. Mit
folgt, daß 1 und 3 benachbart sind. Mit 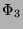 folgt nun, daß entweder 6 oder 7 ein Nachbar von Knoten 3 ist. Mit
folgt nun, daß entweder 6 oder 7 ein Nachbar von Knoten 3 ist. Mit
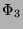 , für den Fall, daß 6 der Nachbar von 3 ist, und mit
, für den Fall, daß 6 der Nachbar von 3 ist, und mit
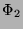 , für den Fall, daß 7 der Nachbar von 3 ist, folgt
dann sofort, daß der Baum von folgender Form ist:
, für den Fall, daß 7 der Nachbar von 3 ist, folgt
dann sofort, daß der Baum von folgender Form ist:
wobei
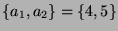 und
und
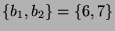 ist. Mit
ist. Mit
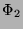 folgt schließlich, daß der letzte Knoten die 2 ist. Es gibt
also die folgenden Brauerbaum-Kandidaten:
folgt schließlich, daß der letzte Knoten die 2 ist. Es gibt
also die folgenden Brauerbaum-Kandidaten:
In [HL89] wird die Möglichkeit
(3.7) mit Hilfe der Green-Korrespondenz für
den zweiten Block ausgeschlossen. In Abschnitt
3.3.4 zeige ich unabhängig
von der Green-Korrespondenz allein mit Hilfe der Kondensation von
Permutationsmoduln, daß dieser Kandidat falsch ist.





Next: Restlicher Beweis zur Rekonstruktion
Up: Primzahl 19, Block 1
Previous: Kondensation
Inhalt
Index
Markus Ottensmann
2000-02-10
![]() folgt, daß 1 und 3 benachbart sind. Mit
folgt, daß 1 und 3 benachbart sind. Mit ![]() folgt nun, daß entweder 6 oder 7 ein Nachbar von Knoten 3 ist. Mit
folgt nun, daß entweder 6 oder 7 ein Nachbar von Knoten 3 ist. Mit
![]() , für den Fall, daß 6 der Nachbar von 3 ist, und mit
, für den Fall, daß 6 der Nachbar von 3 ist, und mit
![]() , für den Fall, daß 7 der Nachbar von 3 ist, folgt
dann sofort, daß der Baum von folgender Form ist:
, für den Fall, daß 7 der Nachbar von 3 ist, folgt
dann sofort, daß der Baum von folgender Form ist: