Grundlagen der Geometrie
Protokoll vom 9.11.00 (AS)

Zurück zum 6.11.00; zur Übungsstunde vom 08.11.00, Teil2;
weiter zur Stunde vom 13.11.00.

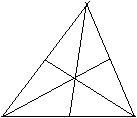
Am Beispiel des Versuchs, den Mittelpunkt einer Seite zu konstruieren, wurde deutlich, daß wir mit unserem bisherigen axiomatischen Aufbau für affine Räume diese Problemstellung nicht lösen können und wir den axiomatischen Aufbau erweitern müssen.
 

Der Mittelpunkt von Zweiecken - oder: Wie kommen die Zahlen in die Geometrie?

Fragen:
1.  Kann ein "Mittelpunkt" durch eine Konstruktion

a) mit einem Parallelogramm oder
b) mit einem Trapez

Zu 2.
a) Beispiele für Aussagen der Geometrie, in denen der Begriff "Mittelpunkt" eine Rolle spielt:

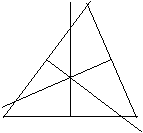
Die drei Seitenhalbierenden eines Dreiecks schneiden sich in einem Punkt.	Verbindet man die Mittelpunkte zweier Seiten eines Dreiecks, so ist die Verbindungsgerade parallel zur dritten Seite des Dreiecks.	Die Mittelpunkte der Seiten eines Tetragons bilden die Eckpunkte eines Parallelo- gramms.

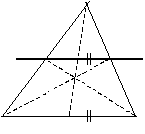
b) Weitere Beispiele, in denen Mittelpunkte verwendet werden (zusammen mit der noch nicht definierten Orthogonalität):

"In der Ebene" läßt sich eine Mittelsenkrechte eindeutig defi- nieren (später).	Die drei Mittelsenkrechten eines Dreiecks schneiden sich in einem Punkt (dem Mittelpunkt des Umkreises).

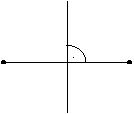
c) Mit Mittelsenkrechten kann der Begriff der "Spiegelung" (in Ebenen) folgendermaßen definiert werden:

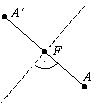Gegeben ist eine Gerade g. Die Spiegelung an g kann so definiert werden: Für Punkte A, die nicht auf g liegen, konstruiere den Fußpunkt F des Lotes von A auf g und wähle den Bildpunkt A' so, daß F der Mittelpunkt von {A, A'} ist; die Punkte auf g bleiben fest. U. a. Drehung, Bewegung und Kongruenz können dann durch Konstruktionen mit Spiegelungen definiert werden.

d)

Kann zu {A, B} ein Punkt C konstruiert werden, so daß B der Mittelpunkt von {A, C} ist (B = MP{A, C})? Diese Konstruktion könnte dann fortgesetzt werden, so daß eine Art "Zahlenstrahl" entsteht.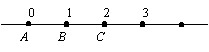

Zu 1. Definitionsversuch mit einer Parallelogrammkonstruktion.
In einem affinen Raum (im Sinne der Axiome) ist ein Zweieck {A, B} gegeben.
Existiert ein Parallelogramm mit der Diagonalen AB?
Nach einigen Versuchen wurde ein solches Parallelogramm konstruiert (s. u.). Bei den vorherigen Versuchen war die Existenz mehrerer Schnittpunkte zu zeigen und die Existenz von mindestens drei Punkten auf einer Geraden nötig. (Z. B. in einem affinen Raum über einem Vektorraum über einen Körper mit nur zwei Elementen können nicht drei Punkte auf einer Geraden liegen. Allerdings macht dies die Suche nach einem Mittelpunkt auch sinnlos.)
 

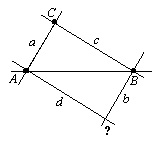Konstruktion: Zeichne eine Gerade b durch B, die nicht gleich AB ist. Bilde eine Gerade a durch A parallel zu b. Wähle einen Punkt C auf a verschieden von A. (Da eine Gerade mindestens zwei Punkten trägt, existiert ein solcher Punkt.) Es sei nun c gleich BC. Die Gerade d parallel zu c ist die vierte Seite des gesuchten Parallelogramms, dessen eine Diagonale AB ist, falls die Existenz des Schnittpunktes von b und d nachgewiesen werden kann.

Existiert der Schnittpunkt von b und d, oder allgemeiner formuliert, existiert zu einem Dreieck {A, B, C} ein vierter Parallelogrammpunkt D, so daß  ein Parallelogramm ist?
Mit unseren bisherigen Axiomen kann dies nicht bewiesen werden. Wir brauchen ein neues (umfassenderes?) Axiom, als das bisherige Veblen-Young-Axiom.

Zurück zur Definition von affinen Räumen.
In affinen Räumen wurden immer wieder Geraden betrachtet, die "nicht windschief" sind. Die Fallunterscheidung in "sind parallel" oder "schneiden sich" war lästig. Um leichter formulieren und beweisen zu können, suchen wir eine geometrische Struktur, in der Parallelen doch einen Schnittpunkt haben.
In der neuen Struktur wird sich auch ein neues Axiom leichter formulieren lassen.

1. Möglichkeit:
Zu gegebener affiner Ebene (Definition "affine Ebene" siehe später) definiere neue Punkte zu Parallelenscharen in der affinen Ebene und eine neue Gerade g_unendl. = Menge der neuen Punkte. Man erhält die Struktur (P', G', I'), in der P' = P vereinigt mit der Menge der neuen Punkte, G' = G vereinigt mit {g_unendl.} und P I' a, falls P I a, wenn P Element von P und a Element von G ist, oder P = P_neu = {x | x || a} ist, oder P = P_neu und a = g_unendl. ist.

2. Möglichkeit: "Völlige Neuerschaffung einer Welt, in der wir affine Ebenen entdecken."
Historischer Hintergrund: Albrecht Dürer - perspektivisches Zeichnen.

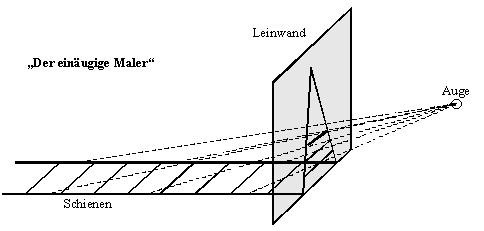
Die Leinwand kann nur einen Teil der Welt darstellen, d. h. die Welt ist auf ihr nicht komplett auf einmal darstellbar. Die "Sehstrahlen" des Auges entsprechen den "neuen Punkten".

Mathematisch kann dieses Modell wie folgt beschrieben werden:
P' = Menge der eindimensionalen Teilräume eines dreidimensionalen Vektorraums V.
G' = Menge der zweidimensionalen Teilräume von V.
I' = ist Teilraum von.

Eine affine Ebene darin sieht folgendermaßen aus:
Wähle einen zweidimensionalen Teilraum U  im Vektorraum V und die Restklassen:
P = x + U,wobei x ein festes Element von V und nicht Element von U ist,
und in x + U wähle Geraden
G = {y + T | T eindimensionaler Teilraum von U, y Element von P};
Für u Element von U gilt x + u I y + T, falls x + u Element von  y + T  ist (d. h. I = Elementsein);
Geraden sind parallel, falls sie Restklassen nach demselben Teilraum sind.

Satz: (P, G, I, ||) ist eine affine Ebene im Sinne der Axiome.
 

Zurück zum 6.11.00; zur Übungsstunde vom 08.11.00, Teil2;
weiter zur Stunde vom 13.11.00.