Grundlagen der Geometrie
Protokoll vom 13.11.2000 (TR)

Zurück zum 9.11.00; weiter zur Übungsstunde vom 15.11.00; zur Stunde vom 16.11.00.

Diese Vorlesung baut auf den Fragestellungen und Motivationen der vorangegangenen Vorlesung auf. Es geht dabei um die Definition eines projektiven Raumes mit Hilfe von Axiomen, die den Axiomen bei affinen Räumen "entsprechen". Es zeigt sich z. B., daß das von uns eingeführte Veblen-Young-Axiom nicht die gewünschten Eigenschaften liefert (bzw. es sich um das falsche handelt) und von daher ebenfalls neu formuliert werden muß.

Definition: Ein projektiver Raum ist eine Inzidenzstruktur (P, G, I) mit den folgenden Eigenschaften (Axiomen).

P1.

Durch je zwei Punkte gibt es genau eine Gerade.

P2.

Auf jeder Geraden liegen mindestens drei Punkte.

P3.

Es gibt drei nicht kollineare Punkte.

P4.

Haben vier Geraden paarweise mindestens fünf Schnittpunkte, so sogar sechs. (Soll heißen: Schneiden sich bei einem Vierseit (Definition später) fünf Geradenpaare, so auch das sechste.) [Vgl. hierzu das affine Veblen-Young-Axiom: Sind bei einem Vierseit fünf Geradenpaare nicht windschief, so auch das sechste (neue Fassung).]
Skizze dazu:

Mit der Neufassung des affinen Veblen-Young-Axioms gelingt dann auch der Beweis des folgenden Satzes.

Satz (über Existenz des vierten Parallelogrammpunktes in affinen Räumen): Zu jedem Dreieck {A, B, C} eines affinen Raumes existiert ein Punkt D, so daß 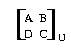ein Parallelogramm ist.

Beweis:
Skizze:

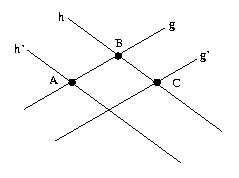
Nach dem affinen Veblen-Young-Axiom (neu!) ist (g´, h´) nicht windschief. Wäre g´ || h´, so g || g´ || h´ || h und B I g und B I h, also g = h nach Axiom A2. Dies heißt, daß A, B, C kollinear sind (auf g = h), was aber im Widerspruch zur Voraussetzung, daß {A, B, C} ein Dreieck ist, steht. Also existiert der Schnittpunkt D von g´ und h´.

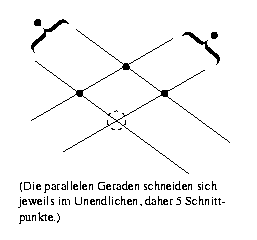
Mit dem Veblen-Young-Axiom läßt sich auch die Existenz des sechsten Schnittpunkts in den folgenden Situationen begründen:

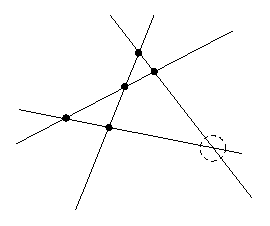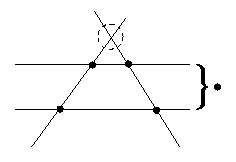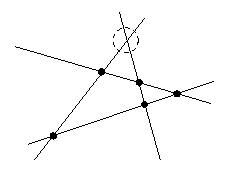Situation 1	Situation 2 (Die parallelen Geraden schneiden sich im Unendlichen.)	Situation 3

In jeder der drei Situationen gibt es fünf Schnittpunkte und damit auch einen sechsten.

Was aber würde in folgender Situation aus dem Axiom folgen?

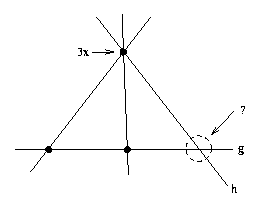
Hier schneiden sich drei Geraden in einem (dreifachen) Schnittpunkt. Stellt man sich diese Situation einmal räumlich vor, so könnte die Gerade h auch "über" oder "unter" der Geraden g verlaufen. Der (sechste) Schnittpunkt existiert in diesen Fällen nicht. Dies ist der Grund dafür, daß in den vorangegangenen Definitionen von einem "Vierseit" die Rede war.

Definition: Ein Vierseit ist eine Menge von vier (!) Geraden, bei der keine drei Geraden durch einen gemeinsamen Punkt gehen.

Satz: Das "alte Veblen-Young-Axiom" ist eine Folgerung aus dem "neuen" (sowohl in affinen als auch in projektiven Räumen).

Beweis: Dieser ist anhand der folgenden Skizze klar:

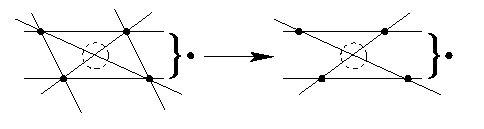
Die Situation des Parallelogrammes wird auf eine mit nur noch vier Geraden reduziert.

Es stellt sich die Frage, ob sich die Diagonalen eines beliebigen Tetragons 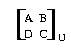schneiden. Dies ist nicht der Fall, man betrachte beispielsweise ein Tetraeder:

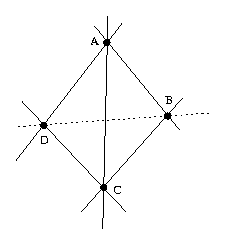
Es ist klar, daß sich die Diagonalen AC, BD hier nicht schneiden.

Eine affine Ebene erfüllt das Fano-Axiom, wenn sich die Diagonalen eines jeden Tetragons 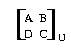(dieser Ebene) schneiden (sie sind ja nach dem Veblen-Young-Axiom (neu) nicht windschief).

Den "kleinen Satz des Pappus" kann man vom affinen in den projektiven Raum "übersetzen". Das bedeutet: Ersetze || durch "Schnitt im Unendlichen". Die Schnittpunkte der parallelen Geraden liegen auf einer Geraden (im Unendlichen).
Skizze des kleinen Satzes von Pappus im projektiven Raum:

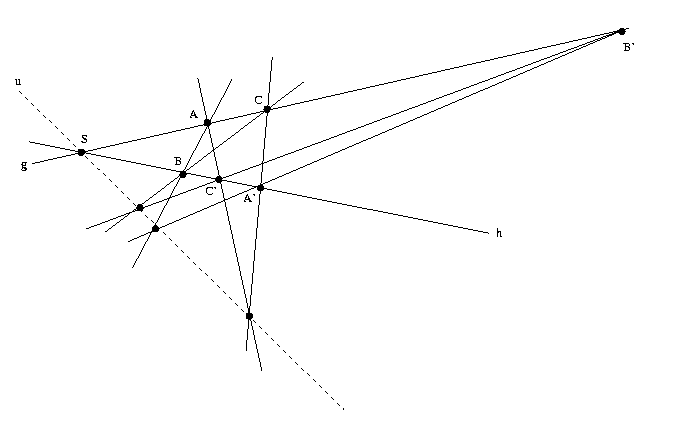
Der kleine Satz von Pappus im projektiven Raum: Gegeben sind zwei sich in S schneidende Geraden g und h (mit g ≠ h), sowie Punkte A, B, C, A´, B´, C´ (die allesamt von S verschieden sind) abwechselnd auf g und h derart, daß es eine Gerade u gibt, auf der sich zwei Paare entsprechender Geraden, nämlich (AB, B´A´) und (BC, B´C´), schneiden. Dann schneiden sich auch CA´ und C´A auf u.

Zurück zum 9.11.00; weiter zur Übungsstunde vom 15.11.00; zur Stunde vom 16.11.00.